Unit - 3
Complex Numbers
If r (cosθ+isinθ) is a complex) number,
Then { r (cosθ+isinθ)}n = rn ( cos(nθ)+isin(nθ))
Or
[ rcisθ]n = rn [ cis(nθ)].
Example: Evaluate ( 1 + i )1000.
Solution:
Let z = 1 + i
We have to represent z in the form of r(cos θ + i sin θ).
Here,
Argument = θ = arc(tan (1/1) = arc tan(1) = π/4
Absolute value = r = (1)2+(1)2=2\sqrt{(1)^2 + (1)^2}= \sqrt{2}(1)2+(1)2=2
Applying DeMoivre’s theorem, we get
z1000 = [√2{cos(π/4) + i sin(π/4)}]1000
= 21000 {cos(1000π/4) + i sin(1000π/4)}
= 21000 {1 + i (0)}
= 21000
Problems on De Moivre’s Identity
Problem 1: Evaluate (2 + 2i)6
Solution: Let z = 2 + 2i
Here, r = 2√2 and θ = 45 degrees
Since z lies in the first quadrant, sinθ and cosθ functions are positive.
Applying De Moivre’s Theorem:
z6 = (2 + 2i)6 = (2√2)6 [cos 450 + i sin 450]6
= (2√2)6 [cos 2700 + i sin 2700]6
= – 512i
Problem 2: Express five fifth‐roots of (√3 + i) in trigonometric form.
Solution:
We know, z = a + ib = r(cos x + i sin x)
Where r = a2+b2\sqrt{a^2+b^2}a2+b2 and tan x = (b/a)
So,
Here r = 2 and θ = 30 degrees
Therefore, z = 2[cos(300 + 3600 k) + i sin cos(300 + 3600 k)]
Applying nth root theorem:
z1/5 = {2[cos(300 + 3600 k) + i sin cos(300 + 3600 k)]}1/5
= 21/5 [cos((300 + 3600 k)/5) + i sin cos((300 + 3600 k)/5)] …(1)
Where k = 0,1,2,3,4
At k = 0; (1)=> z1 = 21/5 [cos 60 + i sin 60]
At k = 1; (1)=> z1 = 21/5 [cos 780 + i sin 780]
At k = 2; (1)=> z1 = 21/5 [cos 1500 + i sin 1500]
At k = 3; (1)=> z1 = 21/5 [cos 2220 + i sin 2220]
At k = 4; (1)=> z1 = 21/5 [cos 2940 + i sin 2940]
Example 1:
Write 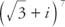 in the form s + bi.
in the form s + bi.
First determine the radius:

Since cos α = 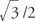 and sin α = ½, α must be in the first quadrant and α = 30°. Therefore,
and sin α = ½, α must be in the first quadrant and α = 30°. Therefore,
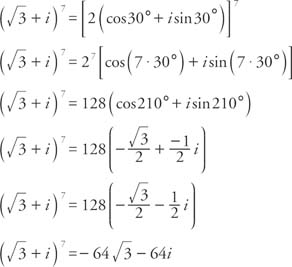
Example 2:
Write 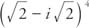 in the form a + bi.
in the form a + bi.
First determine the radius:
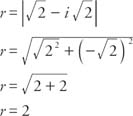
Since cos 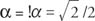 and sin
and sin 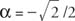 , α must be in the fourth quadrant and α = 315°. Therefore,
, α must be in the fourth quadrant and α = 315°. Therefore,

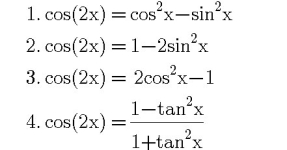
Example
Cos5θ + i sin5θ = cis(5θ) = eⁱ⁵ᶿ = (eⁱᶿ)⁵ = cis⁵(5θ) = (cosθ + i sinθ)⁵
Cos5θ + i sin5θ = cos⁵θ + 5i cos⁴θ sinθ - 10 cos³θ sin²θ - 10i cos²θ sin³θ + 5 cosθ
Sin⁴θ + i sin⁵θ
So, cos5θ = cos⁵θ - 10 cos³θ sin²θ + 5 cosθ sin⁴θ
* In probability theory and statistics, complex random variables are a generalization of real-valued random variables to complex numbers, i.e. the possible values a complex random variable may take are complex numbers. Complex random variables can always be considered as pairs of real random variables: their real and imaginary parts. Therefore, the distribution of one complex random variable may be interpreted as the joint distribution of two real random variables.
Some concepts of real random variables have a straightforward generalization to complex random variables—e.g., the definition of the mean of a complex random variable. Other concepts are unique to complex random variables.
* A complex random variable Z on the probability space ( is a function on Z:
is a function on Z:  ,such that both its real part R(z) and its imaginary part i(z) are real random variables on .
,such that both its real part R(z) and its imaginary part i(z) are real random variables on .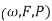 .
.
Circular symmetric complex normal random variables are used extensively in signal processing, and are sometimes referred to as just complex normal in signal processing literature. . Formally, is a standard complex normal random variable.
The characteristic function of complex normal distribution is given by is a n -dimensional complex vector. Central limit theorem. The modulus of a complex normal random variable follows a Hoyt distribution.
Uniform distribution:
Another example of a complex random variable is the uniform distribution over the filled unit circle, i.e. the set . This random variable is an example of a complex random variable for which the probability density function is defined. The density function is shown as the yellow disk and dark blue base in the following figure.
Complex normal distribution:
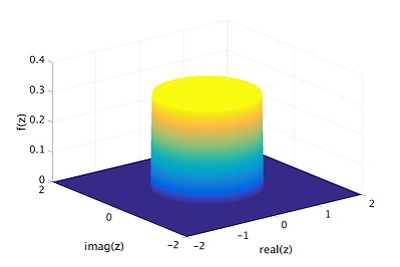
Complex Gaussian random variables are often encountered in applications. They are a straightforward generalization of real Gaussian random variables. The following plot shows an example of the distribution of such a variable.
Cumulative distribution function:
The generalization of the cumulative distribution function from real to complex random variables is not obvious because expressions of the form
P(Z≤1 +3i)make no sense. However expressions of the form P (R(z)≤1, i(z)≤3)
Therefore, we define the cumulative distribution as follow.,
FZ(Z)=FR(Z),I(Z)(R(z),i(z)
Of a complex random variable via the joint distribution of their real and imaginary parts:
Probability density function:
The probability density function of a complex random variable is defined as
fz(z) = fR(z),i(z) (R(z),i(z)) , i.e. the value of the density function at a point (R(z),i(z))
Is defined to be equal to the value of the joint density of the real and imaginary parts of the random variable evaluated at the point  .
.
An equivalent definition is given by
 Fz(z)=
Fz(z)= 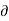 2
2  .P(R(z)≤x ,i(z)≤y), x=R(z) ,y= i(z)
.P(R(z)≤x ,i(z)≤y), x=R(z) ,y= i(z)
As in the real case the density function may not exist.
Examples on functions of a complex variable:
Example 1:
Prove the above-mentioned general property of the operations ∂/∂z and ∂/∂z∗. Hint. Since the formal rules of complex and real algebras are the same, the standard differentiating rules are applicable to complex-valued functions when differentiated with respect to x and y.
Consider the variation, δw, of the function w(z,z∗) corresponding to z →z+δz, where δz = δx+iδy (and implying z∗ →z∗+δz∗, δz∗ = δx−iδy). As can be readily checked with the definitions (16),
δw = δz
∂w ∂z
+δz∗ ∂w ∂z∗
Problem 2:
Note that while δz and δz∗ essentially depend on each other, the expression formally looks like they were independent variables.
Relations for partials in modulus-phase parametrization read: r∂/∂r = x∂/∂x+y∂/∂y = z∂/∂z +z∗∂/∂z∗ , (18) ∂/∂θ = x∂/∂y−y∂/∂x = i(z∂/∂z−z∗∂/∂z∗) , (19) z∂/∂z = (1/2)(r∂/∂r−i∂/∂θ) , z∗∂/∂z∗ = (1/2)(r∂/∂r+i∂/∂θ) .
Hyperbolic Function Definition:
The hyperbolic functions are analogy of the circular function or the trigonometric functions. The hyperbolic function occurs in the solutions of linear differential equations, calculation of distance and angles in the hyperbolic geometry, Laplace’s equations in the cartesian coordinates. Generally, the hyperbolic function takes place in the real argument called the hyperbolic angle. The basic hyperbolic functions are:
- Hyperbolic sine (sinh)
- Hyperbolic cosine (cosh)
- Hyperbolic tangent (tanh)
From these three basic functions, the other functions such as hyperbolic cosecant (cosech), hyperbolic secant(sech) and hyperbolic cotangent (coth) functions are derived. Let us discuss the basic hyperbolic functions, graphs, properties, and inverse hyperbolic functions in detail.
Hyperbolic Functions Formulas
The basic hyperbolic functions formulas along with its graph functions are given below:
Hyperbolic Sine Function
The hyperbolic sine function is a function f: R → R is defined by f(x) = [ex– e-x]/2 and it is denoted by sinh x
Sinh x = [ex– e-x]/2
Graph : y = Sinh x
Hyperbolic Cosine Function
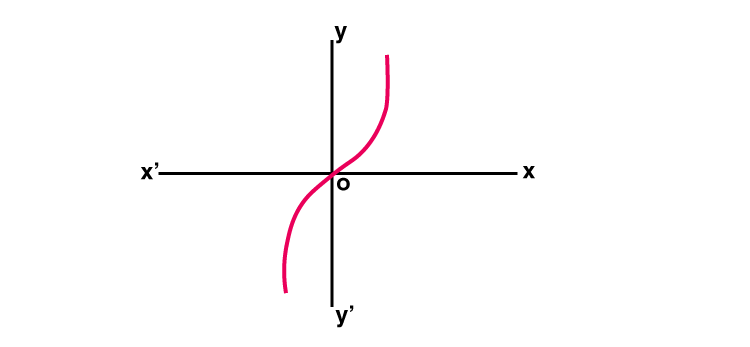
The hyperbolic cosine function is a function f: R → R is defined by f(x) = [ex +e-x]/2 and it is denoted by cosh x
Cosh x = [ex + e-x]/2
Graph : y = cosh x
Hyperbolic Tangent Function
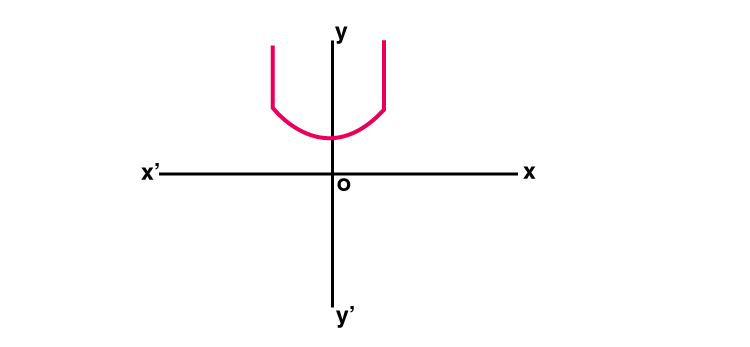
The hyperbolic tangent function is a function f: R → R is defined by f(x) = [ex – e-x] / [ex + e-x] and it is denoted by tanh x
Tanh x = [ex – e-x] / [ex + e-x]
Graph : y = tanh x
Properties of Hyperbolic Functions
The properties of hyperbolic functions are analogous to the trigonometric functions. Some of them are:
- Sinh (-x) = -sinh x
- Cosh (-x) = cosh x
- Sinh 2x = 2 sinh x cosh x
- Cosh 2x = cosh 2x + sinh 2x
The derivatives of hyperbolic functions are:
- d/dx sinh (x) = cosh x
- d/dx cosh (x) = sinh x
Some relations of hyperbolic function to the trigonometric function are as follows:
- Sinh x = – i sin(ix)
- Cosh x = cos (ix)
- Tanh x = -i tan(ix)
Hyperbolic Function Identities
The hyperbolic function identities are similar to the trigonometric functions. Some identities are:
Pythagorean Trigonometric Identities
- Cosh2 (x) – sinh2 (x) = 1
- Tanh2 (x) + sech2 (x) = 1
- Coth2 (x) – cosech2 (x) = 1
Sum to Product
- Sinh x + sinh y = 2 sinh( (x+y)/2) cosh((x-y)/2)
- Sinh x – sinh y = 2cosh((x+y)/2) sinh((x-y)/2)
- Cosh x + cosh y = 2cosh((x+y)/2) cosh((x-y)/2)
- Cosh x – cosh y = 2 sinh((x+y)/2) sinh((x-y)/2)
Product to Sum
- 2sinh x cosh y = sinh(x + y) + sinh(x -y)
- 2cosh x sinh y = sinh(x + y) – sinh(x – y)
- 2sinh x sinh y = cosh(x + y) – cosh(x – y)
- 2cosh x cosh y = cosh(x + y) + cosh(x – y).
Sum and Difference Identities
- Sinh(x ± y) = sinh x cosh x ± coshx sinh y
- Cosh(x ±y) = cosh x cosh y ± sinh x sinh y
- Tanh(x ±y) = (tanh x ± tanh y) / (1± tanh x tanh y )
- Coth(x ±y) = (coth x coth y ± 1) / (coth y ±coth x)
Hyperbolic Function Example
Example: Solve cosh2 x – sinh2 x
Solution:
Given: cosh2 x – sinh2 x
We know that
Sinh x = [ex– e-x]/2
Cosh x = [ex + e-x]/2
Cosh2 x – sinh2 x = [ [ex + e-x]/2 ]2 – [ [ex – e-x]/2 ]2
Cosh2 x – sinh2 x = (4ex-x) /4
Cosh2 x – sinh2 x = (4e0) /4
Cosh2 x – sinh2 x = 4(1) /4 = 1
Therefore, cosh2 x – sinh2 x = 1
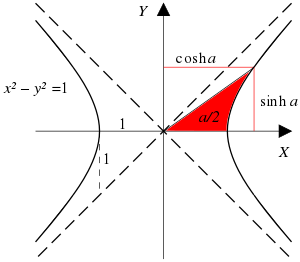
A ray through the unit hyperbola  in the point
in the point  , where
, where  is twice the area between the ray, the hyperbola, and the
is twice the area between the ray, the hyperbola, and the  -axis
-axis
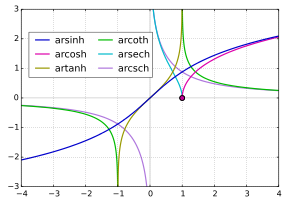
The inverse hyperbolic functions:
The inverse function of hyperbolic functions are known as inverse hyperbolic functions. It is also known as area hyperbolic function. The inverse hyperbolic functions provides the hyperbolic angles corresponding to the given value of the hyperbolic function. Those functions are denoted by sinh-1, cosh-1, tanh-1, csch-1, sech-1, and coth-1. The inverse hyperbolic function in complex plane is defined as follows:
- Sinh-1 x = ln(x + √[1+x2])
- Cosh-1 x = ln(x + √[x2-1])
- Tanh-1 x = (½)[ln(1+x) – ln(1-x)
I
Inverse hyperbolic sine
Inverse hyperbolic sine aka area hyperbolic sine (Latin: Area sinus hyperbolicus):

The domain is the whole real line.
Inverse hyperbolic cosine
Inverse hyperbolic cosine aka area hyperbolic cosine (Latin: Area cosinus hyperbolicus):

The domain is the closed interval [1, +∞ ).
Inverse hyperbolic tangent:
Inverse hyperbolic tangent aka area hyperbolic tangent (Latin: Area tangens hyperbolicus):
The domain is the open interval (−1, 1).
Inverse hyperbolic cotangent:
Inverse hyperbolic cotangent aka area hyperbolic cotangent (Latin: Area cotangens hyperbolicus):
The domain is the union of the open intervals (−∞, −1) and (1, +∞).
Inverse hyperbolic secant:
Inverse hyperbolic secant aka area hyperbolic secant (Latin: Area secans hyperbolicus):
The domain is the semi-open interval (0, 1].
Inverse hyperbolic cosecant:
Inverse hyperbolic cosecant aka area hyperbolic cosecant (Latin: Area cosecans hyperbolicus):
The domain is the real line with 0 removed.
Example 1:
Find the inverse of the function f(x) = ln(x – 2)
Solution:
First, replace f(x) with y
So, y = ln(x – 2)
Replace the equation in exponential way , x – 2 = ey
Now, solving for x,
x = 2 + ey
Now, replace x with y and thus, f-1(x) = y = 2 + ey
Example 2:
To solve an equation: f(x) = 2x + 3, at x = 4
Solution:
We have,
f(4) = 2 × 4 + 3
f(4) = 11
Now, let’s apply for reverse on 11.
f-1(11) = (11 – 3) / 2
f-1(11) = 4
Magically we get 4 again.
Therefore, f(f(4)) = f(4)
So, when we apply function f and its reverse f-1 gives the original value back again, i.e, f-1(f(x)) = x.
Reference Books:
1. Advanced Engineering Mathematics by Erwin Kreyszig, Wiley India Pvt. Ltd.
2. Advanced Engineering Mathematics by H. K. Dass, S. Chand, New Delhi.
3. A text book of Engineering Mathematics Volume I by Peter V. O’Neil and Santosh K.Sengar, Cengage Learning.
4. Mathematical methods of Science and Engineering by Kanti B. Datta, Cengage Learning.
5. Numerical methods by Dr. B. S. Grewal, Khanna Publishers, Delhi.
6. A text book of Engineering Mathematics by N. P. Bali, Iyengar, Laxmi Publications (P) Ltd.,New Delhi.