Unit - 4
Numerical Solution of linear simultaneous equations
Gaussian elimination, also known as row reduction, is an algorithm in linear algebra for solving a system of linear equations. It is usually understood as a sequence of operations performed on the corresponding matrix of coefficients. This method can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix.
Here now we use Gauss-Jordan Elimination method to solve the linear equations in order to get the system of equations.
2X+Y=4
X-3Y=9
X+4Y=-5
 The augmented matrix is.,
The augmented matrix is.,
2 1 4

 1 -3 9 r1 r2
1 -3 9 r1 r2
1 4 -5
 1 -3 9
1 -3 9
2 1 4 -2r1+r2 & -r1+r3
1 4 -5

1 -3 9
0 7 -14 ( 1/7) r2 &( 1/7) r3
0 7 -14

1 -3 9
0 1 -2 -1r2+r3
0 1 -2
1 0 3
0 1 -2
0 0 0
Here the final matrix we has reduced to echelon form and it also represents system of equations with x=3,y=-2.
Gauss-Jordan Method is a popular process of solving system of linear equation in linear algebra. This method solves the linear equations by transforming the augmented matrix into reduced-echelon form with the help of various row operations on augmented matrix.
Gauss Jordan method is unlike gauss elimination as it involves in writing the given linear equation in a form of matrix and to represent the set linear equations into a augmented matrix and making the diagonal elements equal to numeric one. The following are the examples of Gauss -Jordan method.
Example
X+y+z=5
2+3y=5z=8
4x+5z=2
So for the given above set of linear equations the Gauss -Jordan method represents as the following


1 1 1 5
2 3 5 8
4 0 5 2
 The augmented matrix is.,
The augmented matrix is.,
1 1 1
2 3 5
4 0 5
Now we reduce the above matrix in gauss Jordan form.

 2 3 5 r2 r1
2 3 5 r2 r1
 1 1 1 r1 r2
1 1 1 r1 r2
4 0 5

1 2 4 r2 - 2r1
1 1 1
4 0 5
 1 2 4
1 2 4
1 1 1 r3 – r1
3 -2 1
So here represents the guass Jordan method by having a unique number one diagonally in the matrix.
Example 2:
X+y+z=3
2x+3y=7z=0
X+3y-2z=17

 The given set of linear equations can be written as.,
The given set of linear equations can be written as.,
1 1 1 3
2 3 7 0
1 3 -2 17
The augmented matrix o
For the given system of equations is.,

1 1 1
2 3 7
1 3 -2

 1 1 1
1 1 1
7 3 2 c1 c2
-2 3 1

1 1 1
 5 1 0 r2 r2 - 2r1
5 1 0 r2 r2 - 2r1
-2 3 1
So ,here the Gauss -Jordan method completes by making all the diagonal elements to unit number.
Let us consider the system of simultaneous linear equation
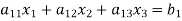
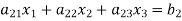 (1)
(1)
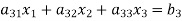
The coefficients of the diagonal elements are larger than the all other coefficients and are non-zero. Rewrite the above equation we get
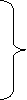
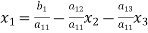
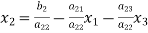 (2)
(2)
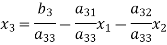
Take the initial approximation 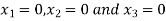 we get the values of the first approximation of
we get the values of the first approximation of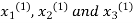 .
.
By the successive iteration we will get the desired the result.
Example1Use Jacobi’s method to solve the system of equations:
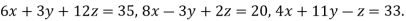
Since 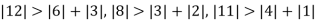
So, we express the unknown with large coefficient in terms of other coefficients.
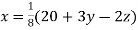
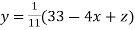 (1)
(1)
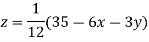
Let the initial approximation be 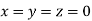
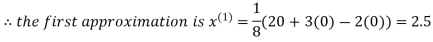
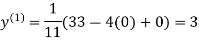
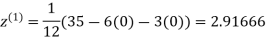
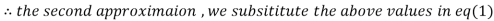
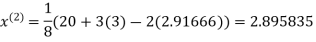
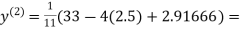 2.35606
2.35606
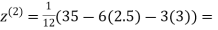 0.91666
0.91666
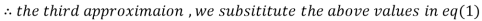
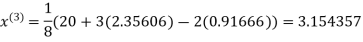
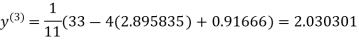
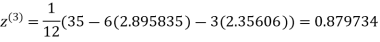
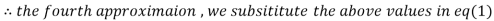
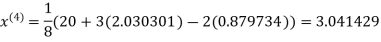
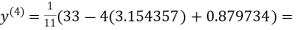 1.932936
1.932936
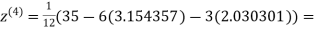 0.831912
0.831912
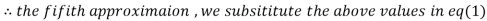
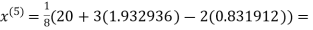 3.016873
3.016873
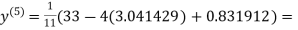 1.969654
1.969654
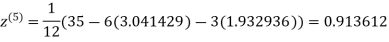
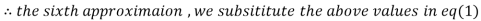
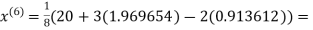 3.010217
3.010217
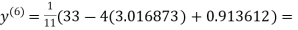 1.986010
1.986010
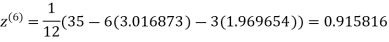
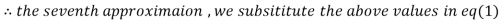
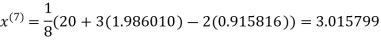
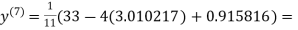 1.988631
1.988631
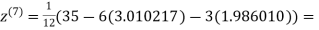 0.915055
0.915055
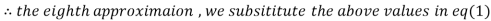
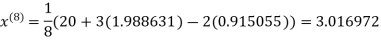
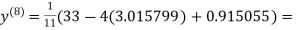 1.986532
1.986532
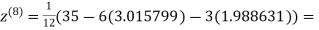 0.911609
0.911609
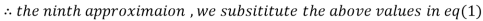
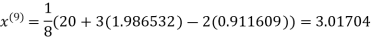
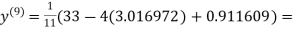 1.985792
1.985792
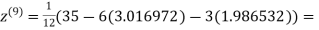 0.911547
0.911547
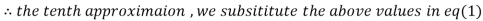
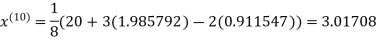
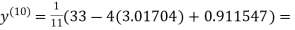 1.98576
1.98576
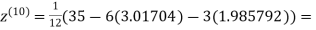 0.911698
0.911698
Since the approximation in ninth and tenth iteration is same up to three decimal places, hence the solution of the given equations is 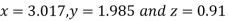
Example2 Solve by Jacobi’s Method, the equations
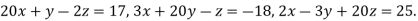
Given equation can be rewrite in the form
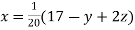 … (i)
… (i)
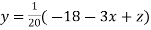 ..(ii)
..(ii)
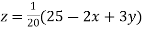 ..(iii)
..(iii)
Let the initial approximation be 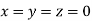
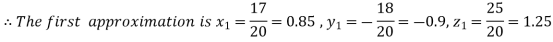
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
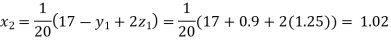
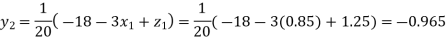
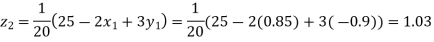
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
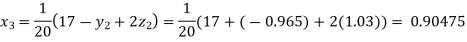
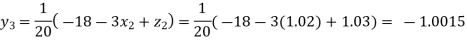
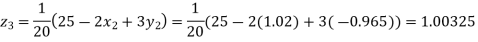
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
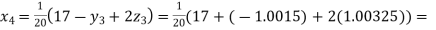 0.90025
0.90025
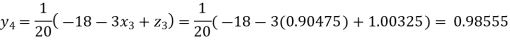
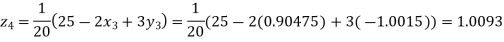
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
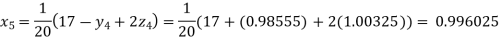
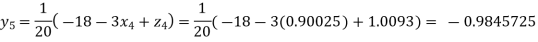
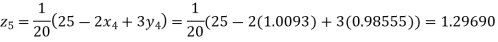
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
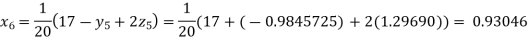
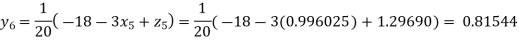
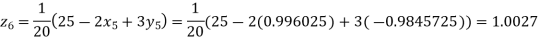
Hence solution approximately is 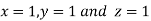
Example3Use Jacobi’s method to solve the system of the equations
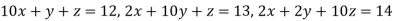
Rewrite the given equations
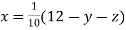
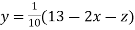 (1)
(1)
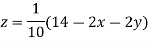
Let the initial approximation be 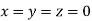
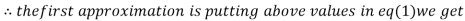
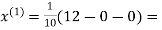 1.2
1.2
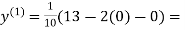 1.3
1.3
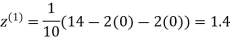
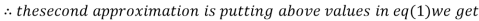
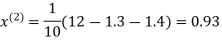
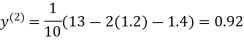
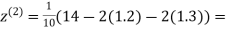 0.9
0.9

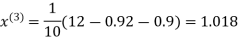
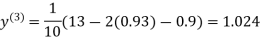
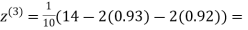 1.03
1.03
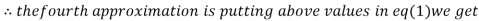
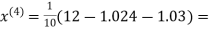 0.9946
0.9946
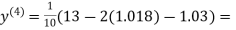 0.9934
0.9934
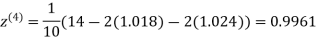

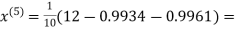 1.0015
1.0015
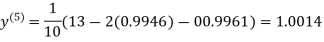
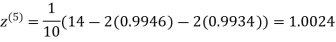
Hence the solution of the above equation correct to two decimal places is
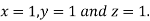
6.3.1
This is the modification of the Jacobi’s Iteration.
Let us consider the system of simultaneous linear equation
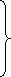
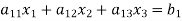
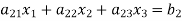 (1)
(1)
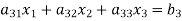
The coefficients of the diagonal elements are larger than the all other coefficients and are non zero. Rewrite the above equation we get
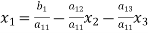
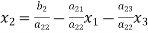 (2)
(2)
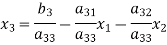
Take the initial approximation 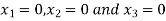 we get the values of the first approximation of
we get the values of the first approximation of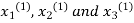 .
.
As above in Jacobi’s Iteration, we take first approximation as
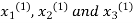 and put in the right hand side of the first equation of (2) and let the result be
and put in the right hand side of the first equation of (2) and let the result be 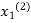 .
.
Now we put 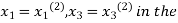 right hand side of second equation of (2) and suppose the result is
right hand side of second equation of (2) and suppose the result is 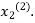
Now put 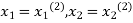 in the RHS of third equation of (2) and suppose the result be
in the RHS of third equation of (2) and suppose the result be 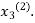
The above method is repeated till the values of all the unknown are found up to desired accuracy.
Example1 Use Gauss –Seidel Iteration method to solve the system of equations
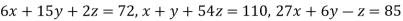
Since 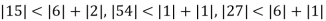
So, we express the unknown of larger coefficient in terms of the unknowns with smaller coefficients.
Rewrite the above system of equations
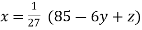
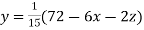 (1)
(1)
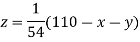
Let the initial approximation be 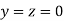
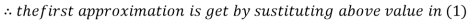
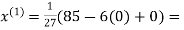 3.14814
3.14814
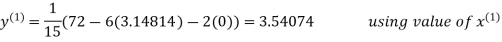
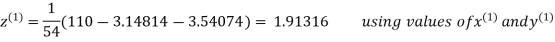
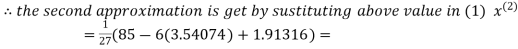 2.43217
2.43217
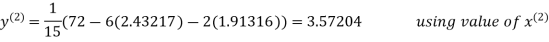
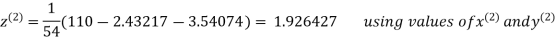
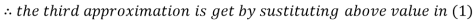
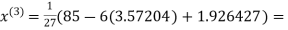 2.42571
2.42571
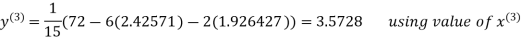
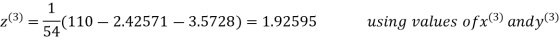
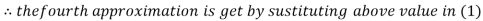
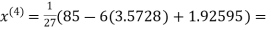 2.4260
2.4260
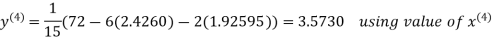
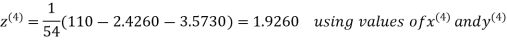
Hence the solution correct to three decimal places is
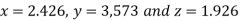
Example2 Solve the following system of equations
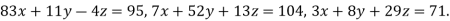
By Gauss-Seidel method.
Rewrite the given system of equations as
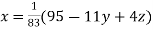
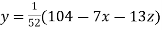 (1)
(1)
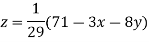
Le t the initial approximation be 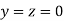
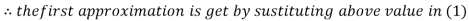
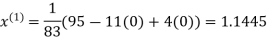
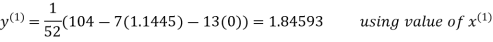
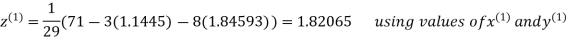
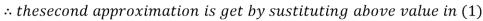
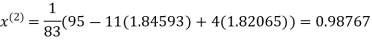
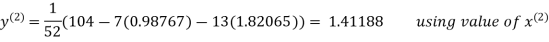
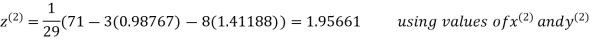
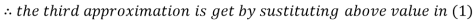
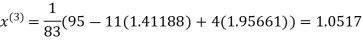
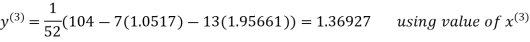
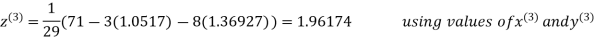
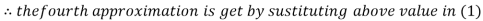
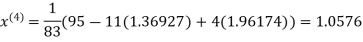
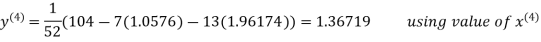
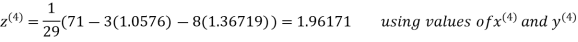
Thus the required solution is 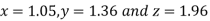
Example3 Solve the following equations by Gauss-Seidel Method
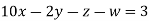
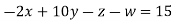
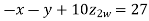
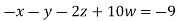
Rewrite the above system of equations
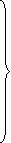
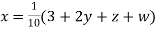
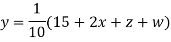
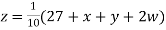 (1)
(1)
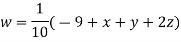
Let the initial approximation be 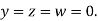

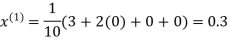
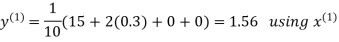
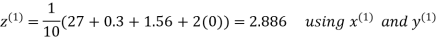
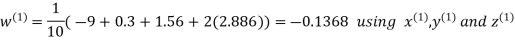

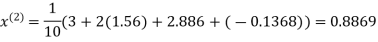
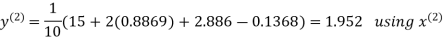
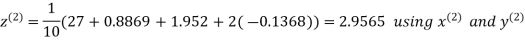
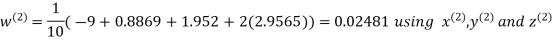

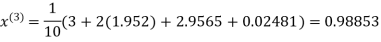
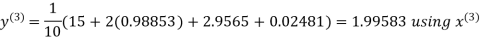
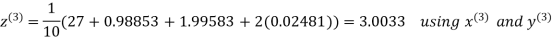
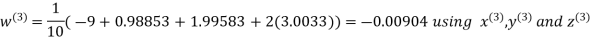

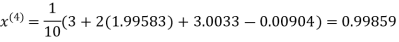
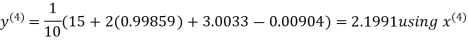
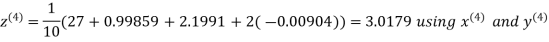
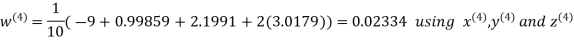

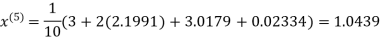
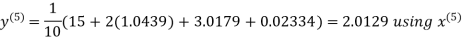
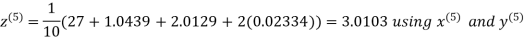
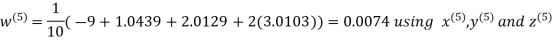
Hence the required solution is 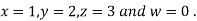
Reference Books:
1. Advanced Engineering Mathematics by Erwin Kreyszig, Wiley India Pvt. Ltd.
2. Advanced Engineering Mathematics by H. K. Dass, S. Chand, New Delhi.
3. A text book of Engineering Mathematics Volume I by Peter V. O’Neil and Santosh K.Sengar,Cengage Learning.
4. Mathematical methods of Science and Engineering by Kanti B. Datta, Cengage Learning.
5. Numerical methods by Dr. B. S. Grewal, Khanna Publishers, Delhi.
6. A text book of Engineering Mathematics by N. P. Bali, Iyengar, Laxmi Publications (P) Ltd.,NewDelhi.