Unit - 5
Expansion of Functions and Indeterminate forms
Maclaurin’s Series Expansions
Statement:-
Maclaurin’s series of f(x) at x = 0 is given by,
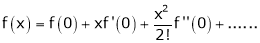
Expansion of some standard functions
i) f(x) = ex then
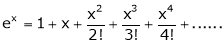
Proof:-
Here
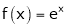
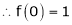
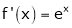
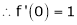
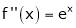

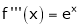
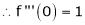
 By Maclaurin’s series we get,
By Maclaurin’s series we get,
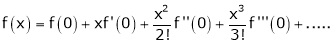
i.e. 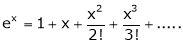
Note that
- Replace x by –x we get

2. f(x) = sin x then

Proof:
Let (x) = sin x
Then by Maclaurin’s series,
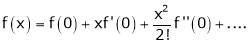 … (1)
… (1)
Since
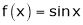

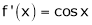
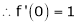
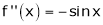
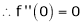


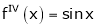

 By equation (i) we get,
By equation (i) we get,
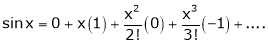
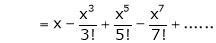
3. 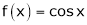 Then
Then
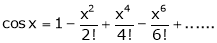
Proof:
Let f(x) = cos x
Then by Maclaurin’s series,
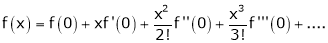 … (1)
… (1)
Since
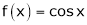
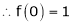
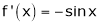
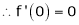


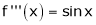
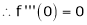


 From Equation (1)
From Equation (1)
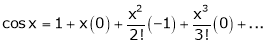
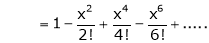
4. 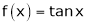 then
then
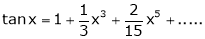
Proof:
Here f(x) = tan x
 By Maclaurin’s expansion,
By Maclaurin’s expansion,
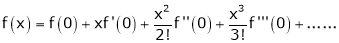 … (1)
… (1)
Since
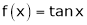
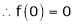
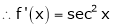
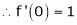
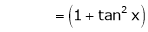

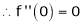


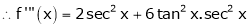
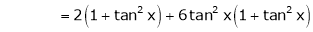
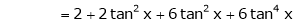
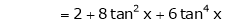
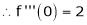
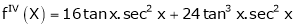
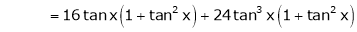
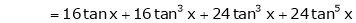
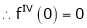
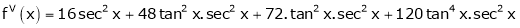
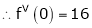 …..
…..
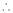 By equation (1)
By equation (1)

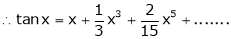
5. 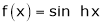 Then
Then

Proof:-
Here f(x) = sin hx.
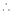 By Maclaurin’s expansion,
By Maclaurin’s expansion,
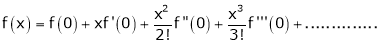 (1)
(1)

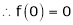
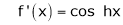
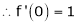
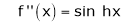

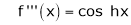
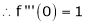
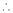 By equation (1) we get,
By equation (1) we get,

6. 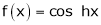 . Then
. Then

Proof:-
Here f(x) = cos hx
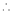 By Maclaurin’s expansion
By Maclaurin’s expansion
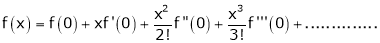 (1)
(1)
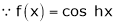
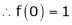
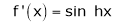
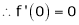

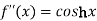
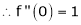
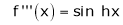
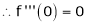
 By equation (1)
By equation (1)
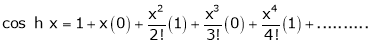
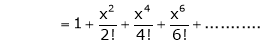
7. f(x) = tan hx
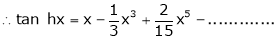
Proof:
Here f(x) = tan hx
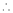 By Maclaurin’s series expansion,
By Maclaurin’s series expansion,
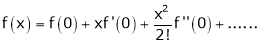 … (1)
… (1)
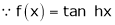
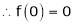
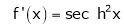
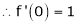
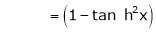
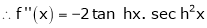
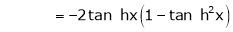

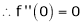
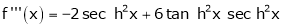
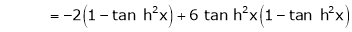
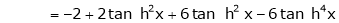
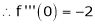


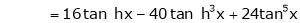
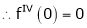
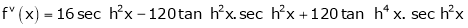
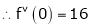
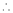 By equation (1)
By equation (1)
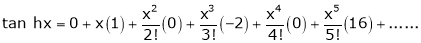

8.  then
then
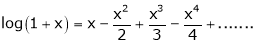
Proof:-
Here f(x) = log (1 + x)
 By Maclaurin’s series expansion,
By Maclaurin’s series expansion,
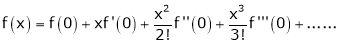 … (1)
… (1)
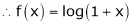
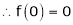
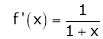
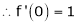
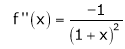
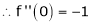
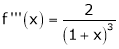

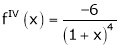

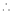 By equation (1)
By equation (1)
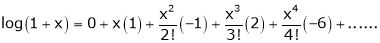

9. 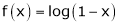
In above result we replace x by -x
Then
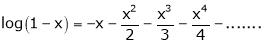
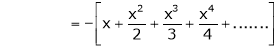
10. Expansion of tan h-1x
We know that
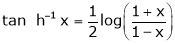
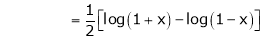
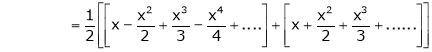
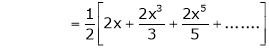

Thus
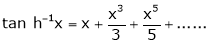
11. Expansion of (1 + x)m
Proof:-
Let f(x) = (1 + x)m
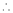 By Maclaurin’s series.
By Maclaurin’s series.
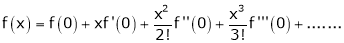 … (1)
… (1)
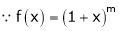
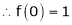
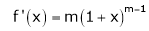
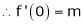
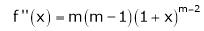
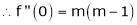
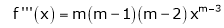
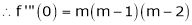
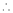 By equation (1) we get,
By equation (1) we get,
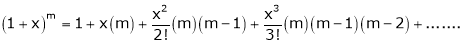
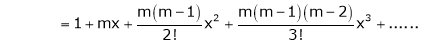
Note that in above expansion if we replace m = -1 then we get,


Now replace x by -x in above we get,
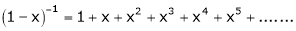
Expand by, Maclaurin’s theorem
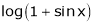
Solution:
Here f(x) = log (1 + sin x)
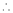 By Maclaurin’s Theorem,
By Maclaurin’s Theorem,
 … (1)
… (1)
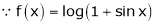
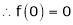
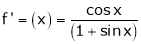
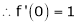
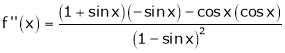
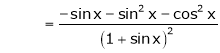
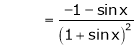
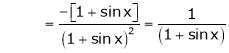
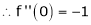
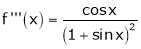
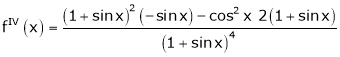
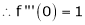
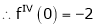 ……..
……..
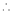 equation (1) becomes,
equation (1) becomes,
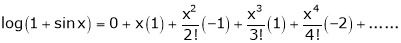
Taylor’s Series Expansion:-
a) The expansion of f(x+h) in ascending power of x is
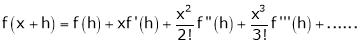
b) The expansion of f(x+h) in ascending power of h is
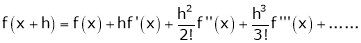
c) The expansion of f(x) in ascending powers of (x-a) is,
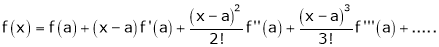
Using the above series expansion we get series expansion of f(x+h) or f(x).
Expansion of functions using standard expansions
Expand 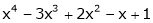 in power of (x – 3)
in power of (x – 3)
Solution:
Let 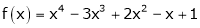
Here a = 3
Now by Taylor’s series expansion,
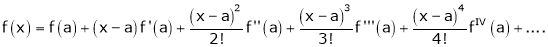 … (1)
… (1)
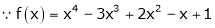

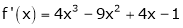
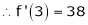
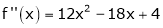
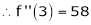
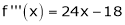
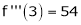
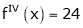
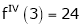
 equation (1) becomes.
equation (1) becomes.
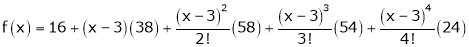

Using Taylors series method expand
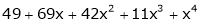 in powers of (x + 2)
in powers of (x + 2)
Solution:
Here 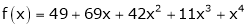
a = -2
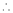 By Taylors series,
By Taylors series,
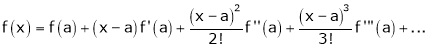 … (1)
… (1)
Since
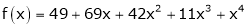
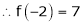
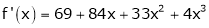
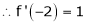
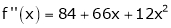


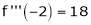
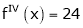
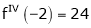 ,
, 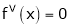 , …..
, …..
Thus equation (1) becomes
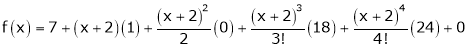
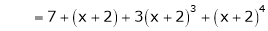
Expand  in ascending powers of x.
in ascending powers of x.
Solution:
Here
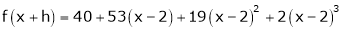
i.e. 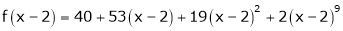
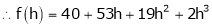
Here h = -2
 By Taylors series,
By Taylors series,
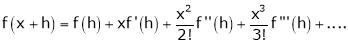 … (1)
… (1)
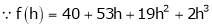
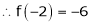
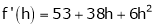
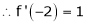
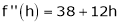
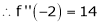
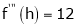
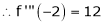
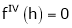

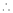 equation (1) becomes,
equation (1) becomes,
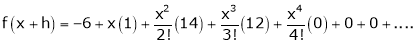
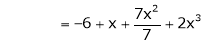
Thus
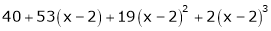
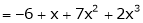
Expand  in powers of x using Taylor’s theorem,
in powers of x using Taylor’s theorem,
Solution:
Here

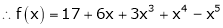
i.e. 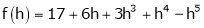
Here
h = 2
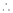 By Taylors series
By Taylors series
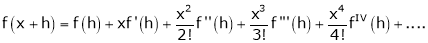 … (1)
… (1)
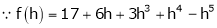
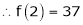
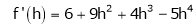
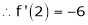
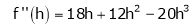
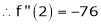
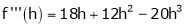
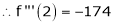
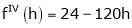
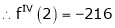
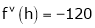
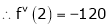
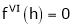
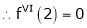
 By equation (1)
By equation (1)
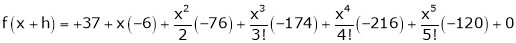
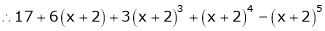
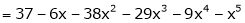
L – Hospital rule for 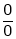 and
and 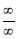
Statement:
If 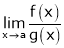 takes either
takes either 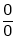 or
or 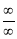
Indeterminate form, then
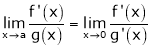 Provided limit is exist
Provided limit is exist
If  again takes either
again takes either 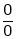 or
or 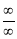 .
.
Then 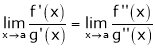 ; limit is exist
; limit is exist
We continue the procedure until the limit is exist.
Exercise 1
Evaluate 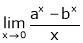
Solution:
Let
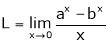 …
… 
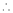 By L – Hospital rule,
By L – Hospital rule,
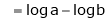
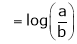
Exercise 2
Evaluate 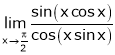
Solution:
Let
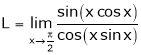 …
… 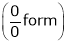
 By L – Hospital rule
By L – Hospital rule
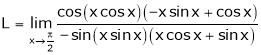
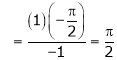
Exercise 3
Evaluate 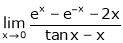
Solution:
Let
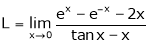 …
… 
 By L – Hospital rule
By L – Hospital rule
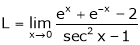 …
… 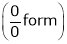
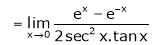 …
… 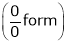
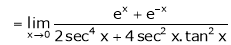
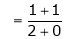

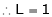
Find the value of a, b if 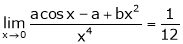
Solution:
Let
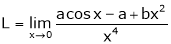 …
… 
 By L – Hospital rule
By L – Hospital rule
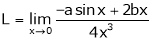 …
… 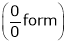
 …
… 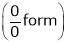
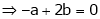 … (1)
… (1)
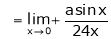 …
… 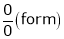
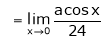
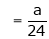
But 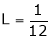
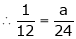

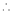 From equation (1)
From equation (1)

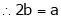
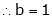
Evaluate 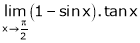
Solution:
Let
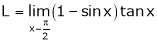 …
… 
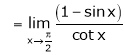 …
… 
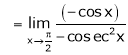 (By L – Hospital Rule)
(By L – Hospital Rule)
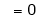
Evaluate 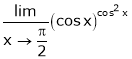
Solution:
Let
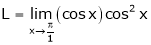 … 0o form
… 0o form
Taking log on both sides we get,
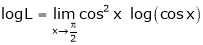 …
… 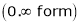
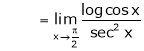 …
… 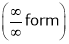
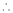 By L – Hospital Rule
By L – Hospital Rule
i.e. 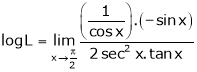
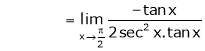
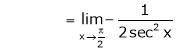

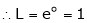
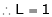
Evaluate 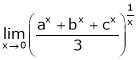
Solution:
Let
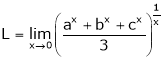 …
… 
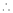 Taking log on both sides,
Taking log on both sides,
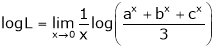
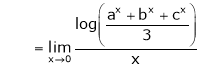 …
… 
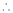 By L – Hospital rule,
By L – Hospital rule,


i.e. 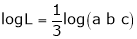
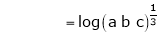
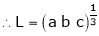
Evaluate 
Solution:
Let
 …
… 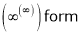
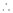 Taking log on both sides, we get
Taking log on both sides, we get
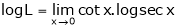
 …
… 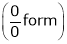
 By L – Hospital Rule,
By L – Hospital Rule,
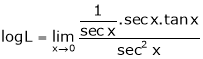
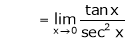

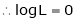
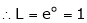
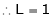
Reference Books:
1. Advanced Engineering Mathematics by Erwin Kreyszig, Wiley India Pvt. Ltd.
2. Advanced Engineering Mathematics by H. K. Dass, S. Chand, New Delhi.
3. A text book of Engineering Mathematics Volume I by Peter V. O’Neil and Santosh K.Sengar, Cengage Learning.
4. Mathematical methods of Science and Engineering by Kanti B. Datta, Cengage Learning.
5. Numerical methods by Dr. B. S. Grewal, Khanna Publishers, Delhi.
6. A text book of Engineering Mathematics by N. P. Bali, Iyengar, Laxmi Publications (P) Ltd.,New Delhi.