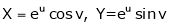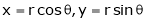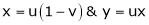Unit 6
Partial Differentiation
Partial Differentiation
If 
Prove that 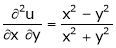
Partial differentiation of function of function
If z = f(u) and 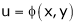 . Then z becomes a function of x & y. In this case z becomes a function of function of x & y.
. Then z becomes a function of x & y. In this case z becomes a function of function of x & y.
i.e.

Then
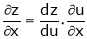 ,
,
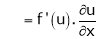
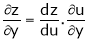

Similarly
If 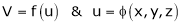
Then z becomes a function of function of x, y & z.
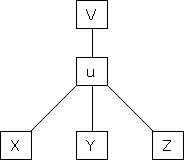
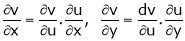
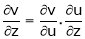 …………….
…………….
- If
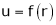 where
where 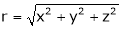
Prove that
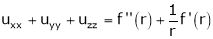
2. If V = 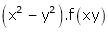 show that
show that
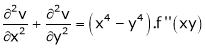
3. If 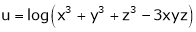 show that
show that
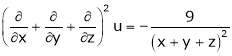
4. If 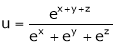 then prove that
then prove that
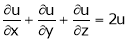
In mathematics, the total derivative of a function 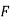 at a point is the best linear approximation near this point of the function with respect to its arguments. Unlike partial derivatives, the total derivative approximates the function with respect to all of its arguments, not just a single one. In many situations, this is the same as considering all partial derivatives simultaneously. The term "total derivative" is primarily used when is a function of several variables, because when is a function of a single variable, the total derivative is the same as the derivative of the function.
at a point is the best linear approximation near this point of the function with respect to its arguments. Unlike partial derivatives, the total derivative approximates the function with respect to all of its arguments, not just a single one. In many situations, this is the same as considering all partial derivatives simultaneously. The term "total derivative" is primarily used when is a function of several variables, because when is a function of a single variable, the total derivative is the same as the derivative of the function.
"Total derivative" is sometimes also used as a synonym for the material derivative in fluid mechanic
A total derivative of a multivariable function of several variables, each of which is a function of another argument, is the derivative of the function with respect to said argument. It is equal to the sum of the partial derivatives with respect to each variable times the derivative of that variable with respect to the independent variable.
In mathematics, an implicit equation is a relation of the form 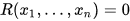 where Ris a function of several variables (often a polynomial). For example, the implicit equation of the unit circle is
where Ris a function of several variables (often a polynomial). For example, the implicit equation of the unit circle is 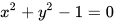 .
.
An implicit function is a function that is defined implicitly by an implicit
Equation, by associating one of the variables (the value) with the others
(the arguments). Thus, an implicit function for yin the context of the unit circle is defined implicitly by 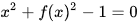 . This implicit equation defines f as a function of y only if
. This implicit equation defines f as a function of y only if 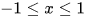 and one considers only non-negative (or non-positive) values for the values of the function.
and one considers only non-negative (or non-positive) values for the values of the function.
The implicit function theorem provides conditions under which some kinds of relations define an implicit function, namely relations defined as the indicator function of the zero set of some continuously differentiable multivariate function.


EXAMPLE 1:
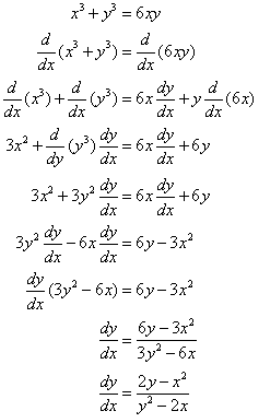
Example 2:
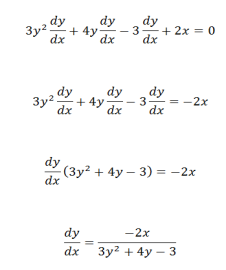
A polynomial in x & y is said to be Homogeneous expression in x & y of degree n. If the degree of each term in the expression is same & equal to n.
e.g.
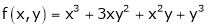 is a homogeneous function of degree 3.
is a homogeneous function of degree 3.
To find the degree of homogeneous expression f(x, y).
- Consider
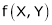
- Put
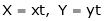 . Then if we get
. Then if we get 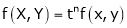 .
.
Then the degree of 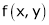 is n.
is n.
Ex.
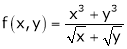
Consider 
Put 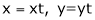

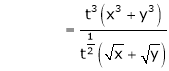
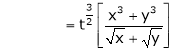
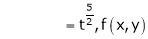 .
.
Thus degree of f(x, y) is 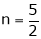
Note that
If 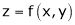 be a homogeneous function of degree n then z can be written as
be a homogeneous function of degree n then z can be written as
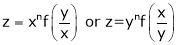
Differentiation of Implicit function
Suppose that we cannot find y explicitly as a function of x. But only implicitly through the relation f(x, y) = 0.
Then we find 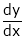
Since 
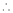 diff. P. w.r.t. x we get
diff. P. w.r.t. x we get

i.e. 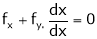
Similarly,
It f (x, y, z) = 0 then z is called implicit function of x, y. Then in this case we get
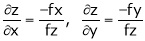
Ex.
Find 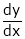 if
if 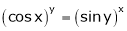
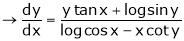
Ex. Find 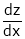 . If
. If 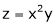 , &
, & 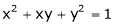
Ex. If  , where
, where 
Find 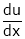
Ex. If 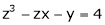
Then find 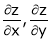
Eulers Theorem on Homogeneous functions:
Statement:
If 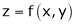 be a homogeneous function of degree n in x & y then,
be a homogeneous function of degree n in x & y then,

Deductions from Eulers theorem
- If
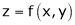 be a homogeneous function of degree n in x & y then,
be a homogeneous function of degree n in x & y then,
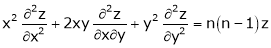 .
.
2. If 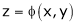 be a homogeneous functions of degree n in x & y and also
be a homogeneous functions of degree n in x & y and also 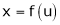 then,
then,
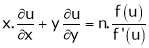
And
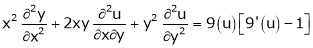
Where 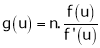
Ex.
If  , find the value of
, find the value of
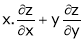
Ex.
If  then find the value of
then find the value of 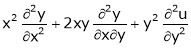
Ex. If 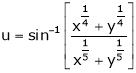 then prove
then prove
That 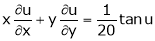
Ex. If 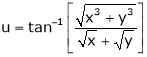 the prove that
the prove that
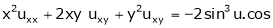
Ex. If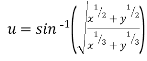 then show
then show
That 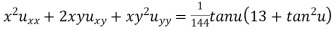
Jacobians, Errors and Approximations, maxima and minima
Jacobians
If u and v be continuous and differentiable functions of two other independent variables x and y such as
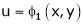 ,
, 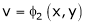 then we define the determine
then we define the determine
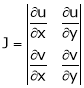 as Jacobian of u, v with respect to x, y
as Jacobian of u, v with respect to x, y
Similarly ,
JJ’ = 1
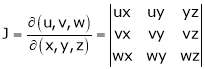
Actually Jacobins are functional determines
Ex.
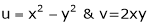 Calculate
Calculate 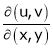
- If
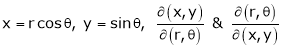
- If
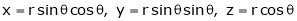
ST 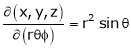
4.  find
find 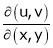
5. If 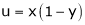 and
and 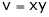 , find
, find 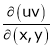
6. 
7. If 
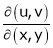
8. If 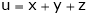 ,
, 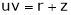 ,
, 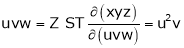
JJ1 = 1
If 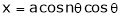 ,
, 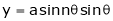
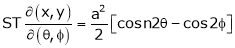
JJ1=1
Jacobian of composite function (chain rule)
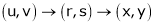
Then 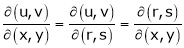
Ex.
- If
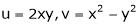
Where 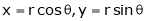
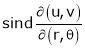
2. If 
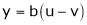 and
and 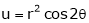

Find 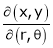
3. If 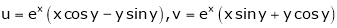
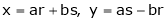
Find 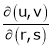
Jacobian of Implicit function
Let u1, u2 be implicit functions of x1, x2 connected by f1, f2 such there
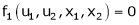 ,
, 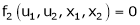
Then 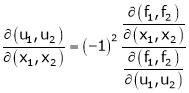
Similarly,
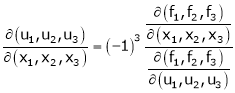
Ex.
If 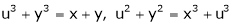

If 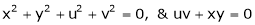
Find 
Partial derivative of implicit functions
Consider four variables u, v, x, y related by implicit function.
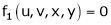 ,
, 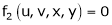
Then
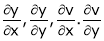
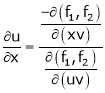

Ex.
If  and
and 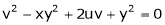
Find 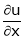
If 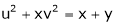 and
and 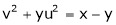
Find 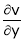
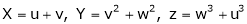
Find 
If 
Find 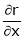
When a function has one variable we know how to find the maxima and minima of the function by differentiating and equating to zero to find the points. But when a function has more than two variables, we use partial differentiation to find the maxima and minima. Where $\lambda $ is Lagrange multiplier.
Maxima and Minima of Functions of Two Variables:
Example 1:
If . . . f ( x , y ) . . . Has a maximum or minimum at point ( a , b ) [ i.e. . . . ( a , b ) . . . Is a point of inflection ], then
f x = 0 . . . And . . . f y = 0 , . . . . . . At ( a , b )
Now put . . . δ f ( a , b ) . . . = . . . f ( a + h , b + k ) – f ( a , b )
So at a maximum or minimum
δ f . . . ≈ . . . h 2 f x x + k 2 f y y + 2 h k f x y
So f has a maximum at ( a , b ) if . . . f x = 0 . . . And . . . f y = 0 , . . . And . . . δ f < 0 for all small h and k . Similarly it has a maximum if . . . δ f > 0 for all small h and k . In particular . . . f xx < 0 . . . And . . . f yy < 0 . . . For a maximum ( putting h = 0 and k = 0 respectively) and . . . f xx > 0 . . . And . . . f yy > 0 . . . For a minimum
The approximation for δ f can be written:
δ f . . . ≈ . ( ( h f xx + k f xy ) 2 – k 2 ( f xy 2 – f xx f yy ) ) ⁄ 2 f xx ,providing . . . f xx ≠ 0.
Or . . δ f . . . ≈ . . . ( Θ 2 – k 2 Δ ) / 2 f xx , . . . Where . . . Θ = ( h f xx + k f xy ) ,
And . . . Δ = ( f xy 2 – f xx f yy ) .
Note that . . . ( Θ 2 – k 2 Δ ) . . . Is positive if Δ is zero or negative, and that Δ is not dependant on the values of h and k . So for a point of inflection we have:
- Δ ≤ 0 . . . And . . . f xx > 0 . . . ⇒ . . . δ f > 0 . . . ⇒ . . . Minimum.
- Δ ≤ 0 . . . And . . . f xx < 0 . . . ⇒ . . . δ f < 0 . . . ⇒ . . . Maximum.
- Δ > 0 . . . Then the value of δ f is dependant on h and k , so this is a saddle-point.
What if f xx = 0 ? . . . Note that the original approximation for δ f is symmetic in x , y , h and k . So we can write
δ f . . . ≈ . . . ( Λ 2 – h 2 Δ ) / 2 f yy , . . . Where . . . Λ = ( k f yy + h f xy ) , . . . Δ same as above.
And note that if . . . f xx = 0 . . . Then Δ is positive, so we will have a saddle-point. A completely symmetric argument holds for f yy = 0.
| Example 2: Determine the critical points and locate any relative minima, maxima and saddle points of function f defined by Solution to Example 1: |