Unit 4
Crystal Physics
Crystal is a homogeneous portion of a crystalline substance, composed of a regular pattern of structural units (ions, atoms or molecules) by plane surfaces making definite angles with each other giving a regular geometric form.
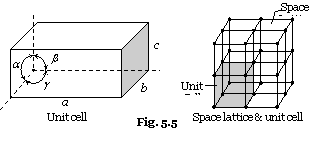
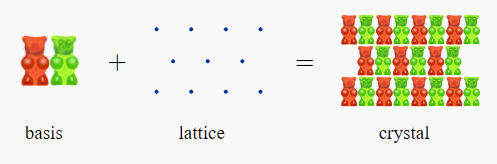
A regular array of points (showing atoms/ions) in three dimensions is commonly called as a space lattice, or lattice.
Each point in a space lattice represents an atom or a group of atoms.
Each point in a space lattice has identical surroundings throughout.
A three-dimensional group of lattice points which when repeated in space generates the crystal called unit cell.
The unit cell is described by the lengths of its edges, a, b, c (which are related to the spacing between layers) and the angles between the edges, 
Lattice:
A lattice is in general defined as a discrete but infinite regular arrangement of points (lattice sites) in a vector space
Bravais Lattice
In solid state physics one usually encounters lattices which exhibit a discrete translational symmetry. If one considers for instance the vector space R3 this means that a translation of the whole lattice by any translation vector given by.

A lattice that can becharacterised inthis way is referred to as a Bravais lattice. All lattice points are equivalent,However, if there are lattice points with different environments they cannot form a Bravais lattice.
Basis:
A basis is a collection of atoms in particular fixed arrangement in space. We could have a basis of a single atom as well as a basis of a complicated but fixed arrangement of hundreds of atoms.
The structure of a crystal can be seen to be composed of a repeated element in three dimensions. This repeated element is known as the unit cell. It is the building block of the crystal structure. We define the unit cell in terms of the lattice (set of identical points). In three dimensions the unit cell is any parallelepiped whose vertices are lattice points, in two dimensions it is any parallelogram whose vertices are lattice points.
So, in general, the unit cell is chosen such that it is the smallest unit cell that reflects the symmetry of the structure. There are two distinct types of unit cell: primitive and non-primitive.
Primitive unit cells contain only one lattice point, which is made up from the lattice points at each of the corners. Non-primitive unit cells contain additional lattice points, either on a face of the unit cell or within the unit cell, and so have more than one lattice point per unit cell.

The seven crystal systems are a method of classifying crystals according to their atomic lattice or structure. The atomic lattice is a three-dimensional network of atoms that are arranged in a symmetrical pattern. The shape of the lattice determines not only which crystal system the stone belongs to, but all of its physical properties and appearance. In some crystal healing practices the axial symmetry of a crystal is believed to directly influence its metaphysical properties. For example, crystals in the Cubic System are believed to be grounding, because the cube is a symbol of the element Earth.
Cubic System

Also known as the isometric system. All three axes are of equal length and intersect at right angles. Based on a square inner structure.
Tetragonal System

Two axes are of equal length and are in the same plane, the main axis is either longer or shorter, and all three intersect at right angles.
Based on a rectangular inner structure.
Hexagonal System

Three out of the four axes are in one plane, of the same length, and intersect each other at angles of 60 degrees. The fourth axis is of a different length and intersects the others at right angles.
Based on a hexagonal (6-sided) inner structure.
Trigonal System

(Rhombohedral System) - Axes and angles in this system are similar to the Hexagonal System, and the two systems are often combined as Hexagonal. In the cross-section of a Hexagonal crystal, there will be six sides. In the cross-section of a Trigonal crystal there will be three sides.
Based on a triangular inner structure.
Orthorhombic System

(Rhombic System)Three axes, all of different lengths, are at right angles to each other.
Based on a rhombic (diamond-shaped) inner structure.
Monoclinic System
There are three axes, each of different lengths. Two are at right angles to each other and the third is inclined.
Based on a parallelogram inner structure.
Triclinic System
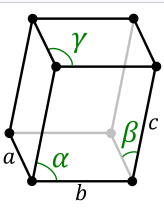
All three axes are of different lengths and inclined towards each other.
Based on a 'triclinic' inner structure, meaning 'three inclined angles'.
Crystal forms are usually paired faces.
- No. Of atom in per unit cell
Primitive or simple cubic unit cell: A unit cell in which all the eight corners of the cube occupied by the particles.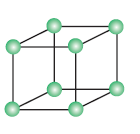
No of atoms present in this unit cell = 8 x 1/8 = 1
Each Corner atom contributes 1/8th portion to the unit cell
Body-cantered cubic unit cell (B.C.C): A unit cell contains one constituent particle present at the centre of each face, along with eight particles at its corners.

No of atoms present in this unit cell = (8 x 1/8) + 1 = 2
(Each Corner atom contributes 1/8th portion to the unit cell)
(Body cantered atom is 1)
Face-centred cubic unit cell (F.C.C): A unit cell contains one constituent particle present at the centre of each face, along with eight particles at its corners.
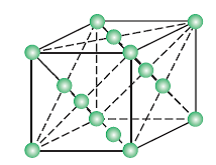
No. Of atoms present in this unit cell = (8 x 1/8) + (6 x ½) = 1 + 3 = 4
(Each Corner atom contributes 1/8th portion to the unit cell)
(Each face cantered atom contributes ½ portion to the unit cell)
The coordination number (CN) is the number of nearest neighbours of a given particle in the crystal lattice. It determines the nature of the bonding in a crystal. The most common coordination numbers are 4, 6, 8, and 12.
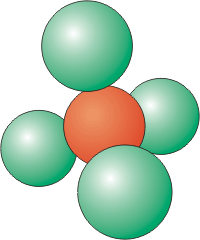
Coordination Number of 4
Four atoms around a central atom are located at the corners of a tetrahedron.
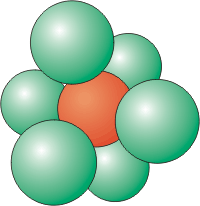
Coordination Number of 6
Six atoms around a central atom are located at the corners of an octahedron. An atom on the corner of a simple cubic unit cell has a coordination number of six.
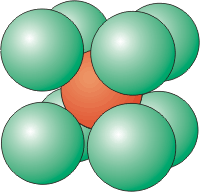
Coordination Number of 8
Eight atoms around a central atom are located at the corners of a cube. The atom in the center of a body-cantered unit cell has a coordination number of eight.
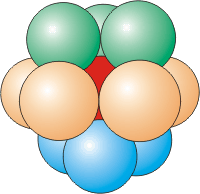
Coordination Number of 12
Each atom in a face-centered cubic unit cell has a coordination number of 12. The 12 particles, which make up the coordination sphere of the red particle lie in three planes.
The radius of an atom is determined from the unit cell edge length (a), which is determined from the location of the atoms, and the assumption that the atoms touch
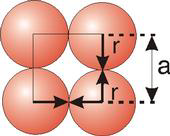
2r=a
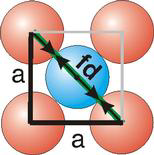
Fd | = | 4r |
|
|
|
|
|
|
Fd2 | = | a2 + a2 |
|
|
|
|
|
|
(4r)2 | = | 2a2 |
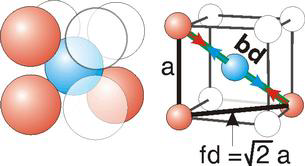
Bd | = | 4r |
|
|
|
|
|
|
Bd2 | = | Fd2 + a2 |
|
|
|
|
|
|
(4r)2 | = | 2a2 + a2 = 3a2 |
Packing efficiency is the fraction of the unit cell that is occupied by particles. Closest packed spheres pack with a packing efficiency of 74%.
Spheres cannot be packed without creating some void space, but the amount of void space depends upon how well they are packed. Packing efficiency (PE) is that fraction of the unit cell volume that is actually occupied by particles, not void space., the packing efficiency of a unit cell is
Packing Efficiency | = |
× 100% | ||
|
|
| ||
|
|
| ||
PE | = |
× 100% |
a = the length of a side of the unit cell, so a3 is the volume of the unit cell.
r = the radius of the atoms that occupy the unit cell, so (4/3) πr3 is the volume of a single atom in the unit cell.
N = the number of atoms in the unit cell, so N (4/3) πr3 is the volume occupied by all of the atoms in the unit cell.
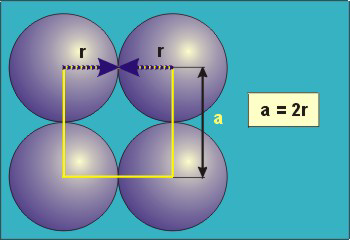
In the simple cubic unit cell, the spheres touch along the cell edge. Consequently, the edge length is two atomic radii
(a = 2r).
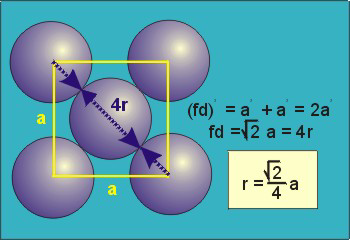
Particle contact in the face-centered cubic unit cell is along the face diagonal (fd). The face diagonal is four atomic radii
(fd = 4r)
The unit cell edge length of a cubic system is calculated using the density of the crystal. Let ‘a’ be the edge length (or primitive) of a cubic unit cell and ‘ρ’ be the density of the crystal.
The mass of the unit cell = ρa3
Let ‘M’ be the molecular weight and NA be the Avogadro number (i.e., number of molecules per kg mole of the substance) of the crystal.
Then, mass of each molecule = 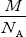
If each unit cell contains n molecules (or lattice points),
Then the mass of unit cell = n 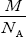
Volume occupied by n atom in a unit cell=
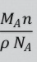
Crystal planes is an important concept used in powder diffraction and crystallography in general. One can imagine a crystal being sub-divided into smaller component units; crystallographers use, depending on context, two alternative sub-divisions: one is the unit cell, the crystal building block, which we will return to later, and the other components are sets of planes invariably known as diffracting planes, reflecting planes, Bragg planes, crystal planes or hkl planes. A set of such planes consists of parallel evenly spaced planes which are extended to exactly fill the entire crystal; each plane is an equal distance, d (the inter-planar spacing), from its neighbouring plane. There are however an infinite number of such types of planes that can be devised and, between them all, they cover every region of space, and indeed every atom, within the crystal: this is one of the properties that makes their concept useful.
It is necessary to have some method of identifying and visualising the most useful planes. Crystallographers use an identification system referred to as Miller, or hkl, indices (a sort of zip-code for the planes).
Miller indices are simply a set of three numbers, hkl, which can take on any combination of three integer values between +∞ and −∞, e.g. (111), (-501) and (7-2-2). Each combination of hkl describes a unique set of planes filling the crystal and so hkl is often presented as a subscript to a property: e.g. dhkl which therefore means the d spacing between the planes defined by hkl. The Miller indices, hkl, also provide a useful means for visualising the planes. The convention is that if you have three axis, x,y,z, with three-unit spacings, a,b,c, on each then one of these hkl planes can be visualised as the plane which intersects the x,y,z-axes at distances of a/h, b/k, c/l respectively
The next such plane parallel to this would pass through the origin. The illustration below shows an example of such a set of planes for the case of hkl = (222)

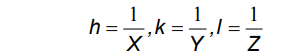
(1) Centre of symmetry : An imaginary point within the crystal such that any line drawn through it intersects the surface of the crystal at equal distances in both directions.

(2) Plane of symmetry: It is an imaginary plane which passes through the centre of a crystal and divides it into two equal portions such that one part is exactly the mirror image of the other.
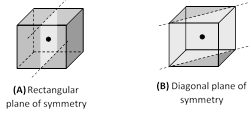
A cubical crystal possesses six diagonal plane of symmetry and three rectangular planes of symmetry.
(3) Axis of symmetry: It is an imaginary straight line about which, if the crystal is rotated, it will present the same appearance more than once during the complete revolution. In general, if the same appearance of a crystal is repeated on rotating through an angle 360/naround an imaginary axis, the axis is called an n-fold axis.
A cubical crystal possesses in all 13 axes of symmetry
Axis of four-fold symmetry = 3 (Because of six faces) | Axis of three-fold symmetry = 4 (Because of eight corners) | Axis of two-fold symmetry = 6 (Because of twelve edges) |
 |  |  |
(4) Elements of symmetry : The total number of planes, axes and centre of symmetry possessed by a crystal are termed as elements of symmetry. A cubic crystal possesses a total of 23 elements of symmetry.
Planes of symmetry
= (3+6) =9
,
Axes of symmetry
= (3+4+6) =13
,
Centre of symmetry = 1.
Total number of symmetry elements = 23
Bragg’s Law can be derived using simple geometry by considering the distances travelled by two parallel X-rays reflecting from adjacent planes. The X-ray hitting the lower plane must travel the extra distance AB and BC. To remain in phase with the first X-ray, this distance must be a multiple of the wavelength thus:
nλ = AB+BC = 2AB (since the two triangles are identical)
The distance AB can be expressed in terms of the interplanar spacing (d) and incident angle (θ) because d is the hypotenuse of right triangle ZAB shown at right.
Sin(θ) = AB/d
Thus AB = d sin(θ)
Therefore:
nλ = 2 d sin(θ)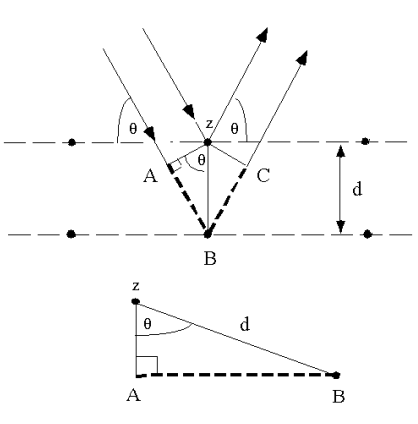
Reflection (signal) only occurs when conditions for constructive interference between the beams are met
These conditions are met when the difference in path length equals an integral number of wavelengths, n. The final equation is the
BRAGG’S LAW n λ = 2 d sin θ
