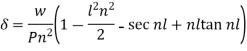Unit–1
Linear differential equations with constant coefficients
The linear homogeneous differential equation of the nth order with constant coefficients can be written as
y(n) (x) + a1y(n-1)(x)+.....+an-1y’(x)+any(x) =0
Where a1, a2 ...... anare constants which may be real or complex.
Using the linear differential operator L(D), this equation can be represented as
L (D) y(x)=0,
Where
L (D)=Dn+ a1D(n-1)+⋯+an-1D+an.
Example 1:
Solve the differential equation y’’’+2y’’-y’-2y=0
Solution:
The corresponding characteristic equation is,
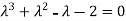
Solving it, we find the roots

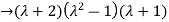 =0
=0
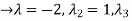 =-1
=-1
The general solution for the differential equation is
Y(x)=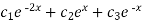
Where 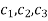 are arbitrary constants.
are arbitrary constants.
Example 2:
Solve the equation y’’’+11y’-5y=0
Solution:
The characteristic equation of the give D.E is
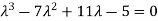
Here one of the root is 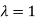 then factorising the term
then factorising the term 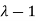 from the equation we obtain
from the equation we obtain
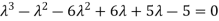
 (
( (
(
 (
(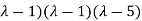 =0
=0
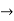 (
(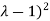 (
(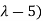 =0
=0
Thus the equation has two roots 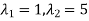
Hence the general equation of the D.E is
Y(x)=(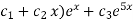
Where 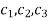 are arbitrary constants.
are arbitrary constants.
Complementary Function, Particular Integral
- A function which satisfies the L.D.E F(D)y=0 is known as complementary function of L.D.E
- A function which satisfies the L.D.E F(D)y=Q is known as complementary function of L.D.E
- The general solution of L.D.E for F(D)y = Q is given by
Y= C.F + P.I
Rules for finding complementary function-
To solve the equation- 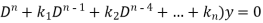
Where  (co-efficient equated to zero) ……. (1)
(co-efficient equated to zero) ……. (1)
Is called auxiliary equation.
Suppose  are the roots.
are the roots.
First case- If all the roots are real and different, then equation (1) will be-
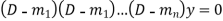 …………….. (2)
…………….. (2)
Then the complete solution is- 
Second case- If two roots are equal (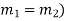
The complete solution is-
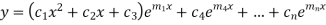
Third case- If one pair of roots be imaginary that means 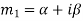 and
and 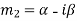 , then the complete solution is-
, then the complete solution is-
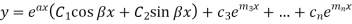
Fourth case- If two points of imaginary roots are equal that means 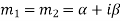 and
and 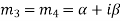 , then the complete solution is-
, then the complete solution is-
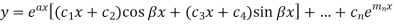
Example-1: Solve-
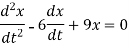
Sol. The given equation can be written in the symbolic form as-
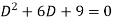
So that A.E is 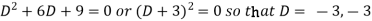
Hence the complete solution is-
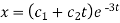
Example 2:
Determine the complementary function for the following D.E
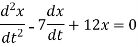
At t=0,1
Solution:
We can write the given homogeneous equation as follows

The auxiliary equation is 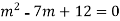
By factorising the auxiliary equations we get,
(m-3)(m-4)=0
And the two real solutions are m=3,4
Hence the complementary function is,
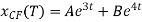
Since f(t) = 2 then  = c
= c
 12c=2
12c=2
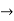 c=1/6 and
c=1/6 and  = 1/6
= 1/6
Therefore the general solution is
X(t) = 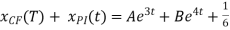
Example 3:
Solve 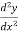 -
-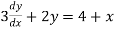
Given y=4,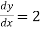 when x=0
when x=0
Solution:
The auxiliary equation is

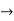 (m-1)(m-2)=0
(m-1)(m-2)=0
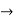 m=1,2
m=1,2
Therefore complimentary function is,

The particular integral is given by y=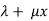
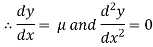
Substituting the above values in given equation we get,
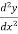 -
-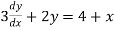 = 0-3
= 0-3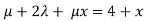
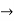 by comparing the co-efficients we get 2
by comparing the co-efficients we get 2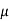 =1
=1  = ½
= ½
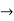 -3
-3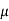 + 2
+ 2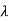 = 4+x
= 4+x
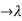 = 11/4
= 11/4
Therefore P.I is,
11/4+(1/2)x
General solution is, y = A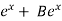 + 11/4 +1/2x
+ 11/4 +1/2x
Rules to find the particular integral-
Consider the equation 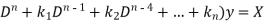
So that
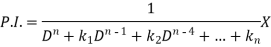
Case-1: when 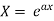
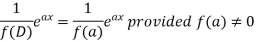
When 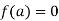 , then the above method fails.
, then the above method fails.
So that in this case-

If f’(a) = 0 then
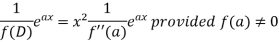
Case-2: when 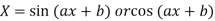
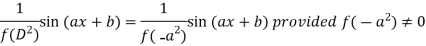
When 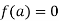 , then the above method fails.
, then the above method fails.
So that in this case-
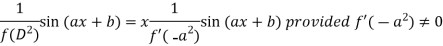
If f’(a) = 0 then
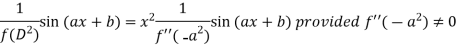
Case-3: when 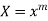
P.I. = 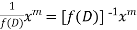
Case-4: when 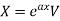 here V is the function of x.
here V is the function of x.
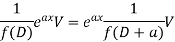
Case-5: When X is any function of x.
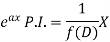
Example-1: Find P.I of 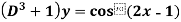
Sol. P.I. = 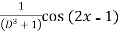
Put 
= 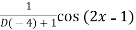
Multiply and divide by 1+4D
= 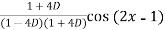
= 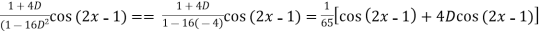
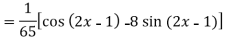
Example-2: Find the P.I. Of 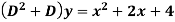
Sol. P.I. = 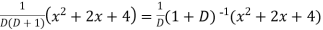

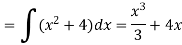
Example-3: Find P.I. Of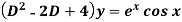
Sol. P.I = 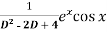
Replace D by D+1
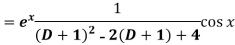
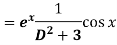
Put 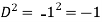

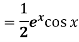
Method of variation of parameters
Consider a second order LDE with constant co-efficients given by
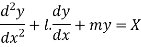
Then let the complimentary function  is given by
is given by
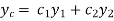
Then the particular integral is
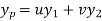
Where u and v are unknown and to be calculated using the formula
u=
Example-1: Solve the following DE by using variation of parameters-
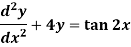
Sol. We can write the given equation in symbolic form as-
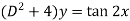
To find CF-
It’s A.E. Is 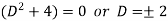
So that CF is- 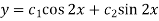
To find PI-
Here 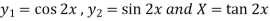
Now 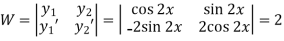
Thus PI = 
= 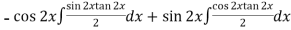
= 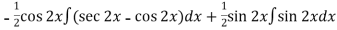
= 
= 
So that the complete solution is-
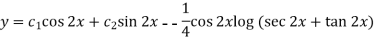
Example-2: Solve the following by using the method of variation of parameters.
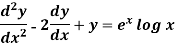
Sol. This can be written as-
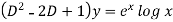
C.F.-
Auxiliary equation is- 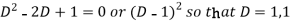
So that the C.F. Will be- 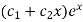
P.I.-
Here 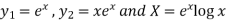
Now 
Thus PI = 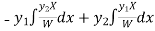
= 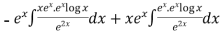
= 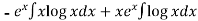
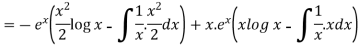
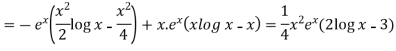
So that the complete solution is-
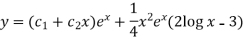
Beam-
Beam can be capable of withstanding loads in bending. The beam shape can be described by a linear differential equation.
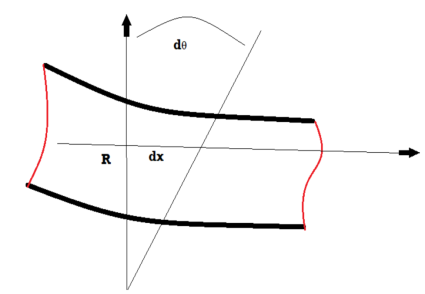
For a bending beam, the angle dθappears between two adjacent sections spaced at distance dx.
The deformation ε at each point is proportional to the y-axis.

Here R is the radius of curvature of the beam.
The magnitude of the normal stress σ in the cross section will also depend on y-axis.
It can be given by the following equation (Hook’s law)-
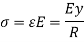
Here E is the modulus of elasticity of the beam.
The bending moment M(x) for a section of the beam which is related to z-axis is-
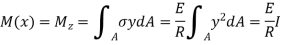
It is known as Bernoulli-Euler formula.
Here,
E = Modulus of elasticity of the beam
I = Moment of inertia of the cross-section about z-axis.
R = radius of the curvature of the elastic curve.
In case of small deflection in beam, the slope of the elastic curve is also small.
Therefore we may not consider 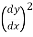 in the formula-
in the formula-
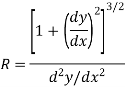
So for small deflections-
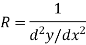
Here I is the moment of inertia of the cross section with respect to the z-axis
Hence the bending moment is given by-

Shear force is given as-
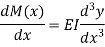
And intensity of loading-
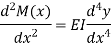
1. Convention of signs-
Due to external forces on the left of the section, the sum of the moment about a section NN’, if anti-clockwise is taken as positive and if clockwise is taken as negative.
2. End conditions-
1. At a freely supported end- there being no bending moment and no deflection, we have y = 0 and 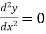
2. At a fixed horizontal end, the deflection and the slope of the beam being both zero, we have y = 0 and dy/dx = 0.
3. At a perfectly free end, there being no bending moment or shear force, we have-
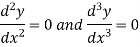
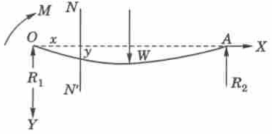
Example: A cantilever beam of length ‘l’ and weighing w lb/unit is subjected to a horizontal compressive force P applied at the free end. Taking the origin at the free end and y-axis upwards, establish the differential equation of the beam and then find the maximum deflection.
Sol.
Suppose N(x,y) be any point of the beam referred to axes through the free end.
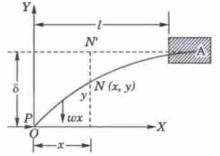
The external forces acting to the left of the section NN’, are-
1. The compressive force P,
2. The weight of the portion ON = wx acting midway.
We get, taking moments about N,
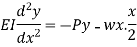
Or
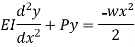
Which is the differential equation.
By taking 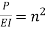 and dividing by EI, we get-
and dividing by EI, we get-

The auxiliary equation is-
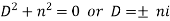
Here we get-
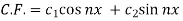
Now-
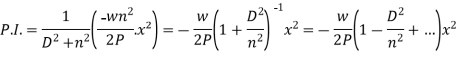
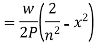
So that the complete solution of the differential equation will be-
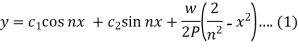
The boundary conditions at the fixed end are-

By using this condition equation (1) becomes-

On differentiating equation (1), we get-
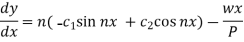
Apply the second condition, it gives-
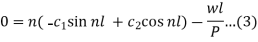
Imposing the boundary condition for the free end- (x = 0 and  on-
on-
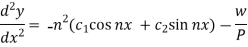
We get-

Put these values in equation (3), we get-
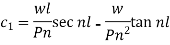
Now put these values in (2), we get-
The maximum deflection-