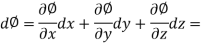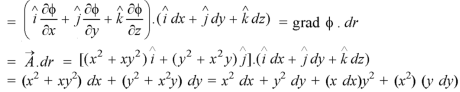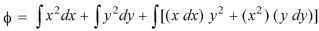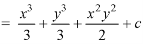UNIT–2

Vector differential calculus

2.1. Differentiation of vectors Consistency of linear system equations

Vector function- A vector function can be defined as below-

If a vector ‘r’ is a function of a scalar variable ‘t’, then-

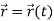
We define the derivative of a vector function as-

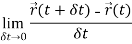
We can denote it as-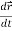

Similarly 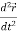is the second order derivative of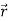

Note- 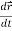gives the velocity and 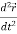gives acceleration.

Rules for differentiation-

1.

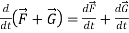
2.

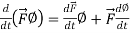
3.

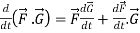
4.

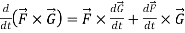
5.

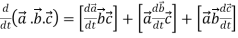
Example-1: A particle moves along the curve 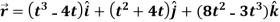, here ‘t’  is the time. Find its velocity and acceleration at t = 2.

Sol. Here we have-

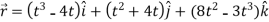
Then, velocity

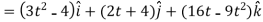
Velocity at t = 2,

=

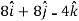
Acceleration =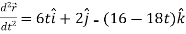

Acceleration at t = 2,

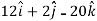
Example-2: If 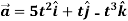and 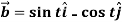then find-

1.

2.

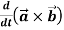
Sol. 1. We know that-

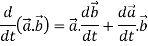
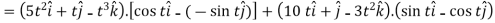
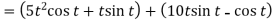
2.

2.2. Gradient of scalar point function and directional derivative

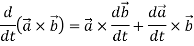
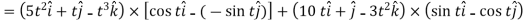
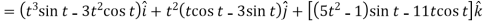
Suppose f(x, y, z) be the scalar function and it is continuously differentiable then the vector-

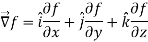
Is called gradient of f and we can write is as grad f.

So that-

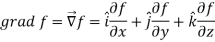
Here 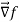is a vector which has three components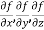

Properties of gradient-

Property-1: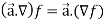

Proof:

First we will take left hand side

L.H.S =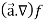

=

=

=

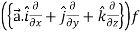
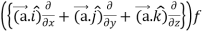
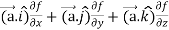
Now taking R.H.S,

R.H.S. =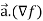

=

=

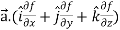
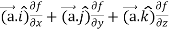
Here-                     L.H.S. = R.H.S.

Hence proved.

Property-2: Gradient of a constant (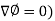

Proof:

Suppose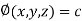

Then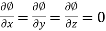

We know that the gradient-

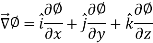
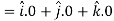
= 0

Property-3: Gradient of the sum and difference of two functions-

If f and g are two scalar point functions, then

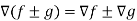
Proof:   

L.H.S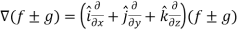                                

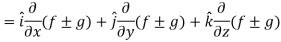
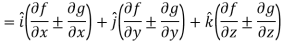
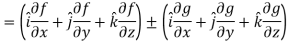
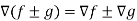
Hence proved

Property-4: Gradient of the product of two functions

If f and g are two scalar point functions, then

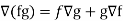
Proof:

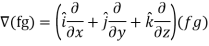
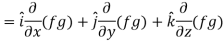
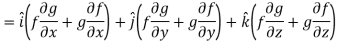
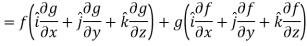
So that-

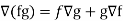
Hence proved.

Property-5: Gradient of the quotient of two functions-

If f and g are two scalar point functions, then-

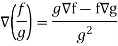
Proof:

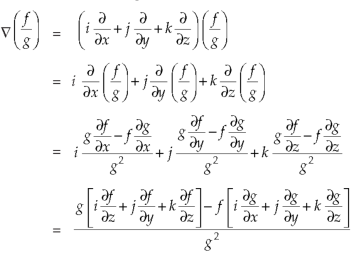
So that-

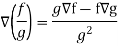
Example-1: If 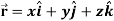, then show that

1.

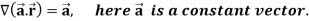
2.

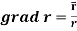
Sol.

Suppose 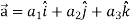  and

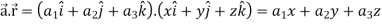
Now taking L.H.S,

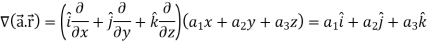
Which is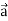

Hence proved.

2.

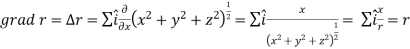
So that

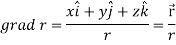
Example: If 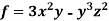then find grad f at the point (1,-2,-1).

Sol.

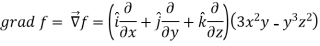
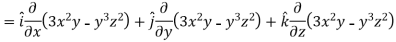
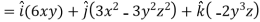
Now grad f at (1 , -2, -1) will be-       

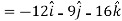
Example: If 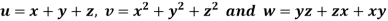then prove that grad u , grad v and grad w are coplanar.

Sol.

Here-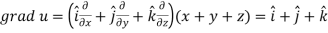                     

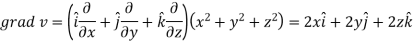
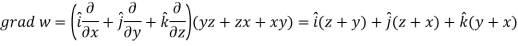
Now-

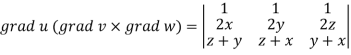
Apply

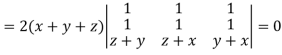
Which becomes zero.

So that we can say that grad u, grad v and grad w are coplanar vectors.

Directional derivative-

Let ϕ be a scalar point function and let ϕ(P) and ϕ(Q) be the values of ϕ at two neighbouring points P and Q in the field. Then,

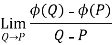
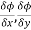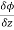,are the directional derivative of ϕ in the direction of the coordinate axes at P.

The directional derivative of ϕ in the direction l, m, n=l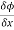 + m+

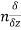
The directional derivative of ϕ in the direction of =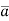

Example: Find the directional derivative of 1/r in the direction 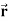where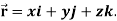

Sol. Here

Now,

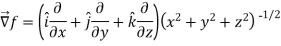
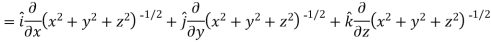
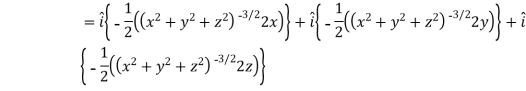
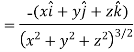
And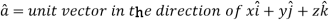

We know that-

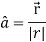
So that-

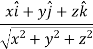
Now,

Directional derivative =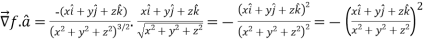

Example: Find the directional derivative of

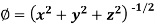
At the points (3, 1, 2) in the direction of the vector .

Sol. Here it is given that-

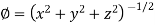
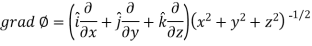
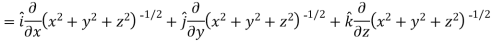
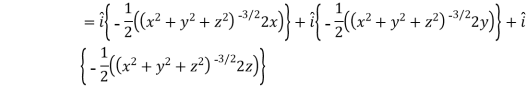
Now at the point (3, 1, 2)-

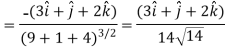
Let 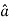be the unit vector in the given direction, then

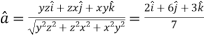at (3, 1, 2)

Now,

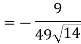
Example: Find the directional derivatives of 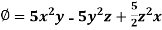at the point P(1, 1, 1) in the direction of the line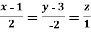

Sol. Here

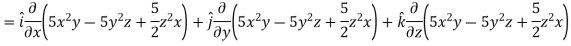
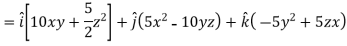
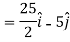
Direction ratio of the line 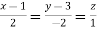are 2, -2, 1

Now directions cosines of the line are-

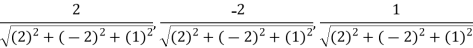
Which are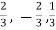

Directional derivative in the direction of the line-

2.3. Divergence and curl of vector point function and solenoidal vector fields

Divergence (Definition)-

Suppose 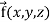is a given continuous differentiable vector function then the divergence of this function can be defined as-

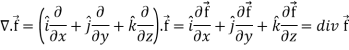
Curl (Definition)-

Curl of a vector function can be defined as-

Note- Irrotational vector-

If 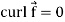then the vector is said to be irrotational.

Vector identities:

Identity-1:  grad uv = u grad v + v grad u

Proof: 

So that

Graduv = u grad v + v grad u

Identity-2: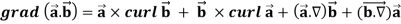 

Proof:

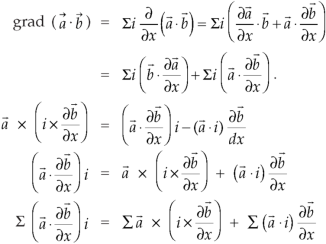
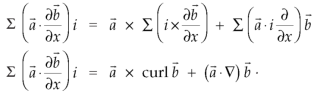
Interchanging , we get-

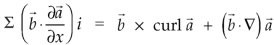
We get by using above equations-

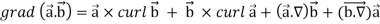
Identity-3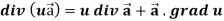

Proof: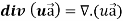   

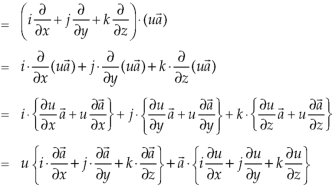
So that-

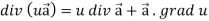
Identity-4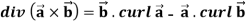

Proof:

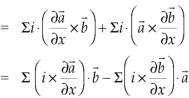
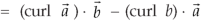
So that,

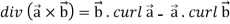
Identity-5                  curl (u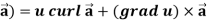

Proof:

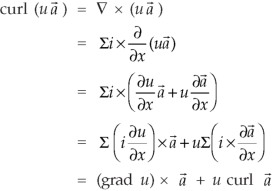
So that

Curl (u

Identity-6: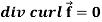

Proof:

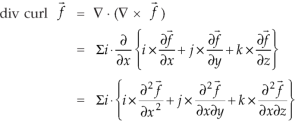
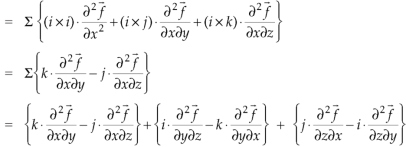
So that-

Identity-7:

Proof:

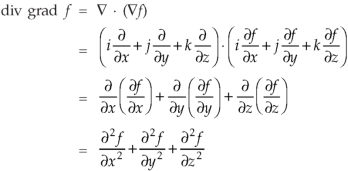
So that-

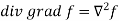
Example-1: Show that-

1.

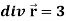
2.

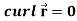
Sol. We know that-

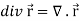
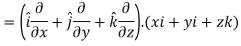
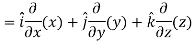
2. We know that-

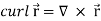
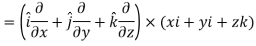
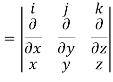
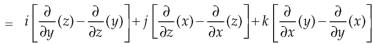
= 0

Example-2: If 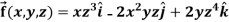then find the divergence and curl of .

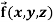Sol.  we know that-

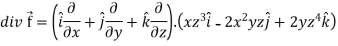
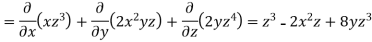
Now-

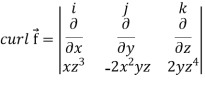
Example-3: Prove that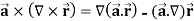

Note- here 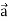is a constant vector and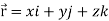

Sol. Here 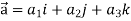   and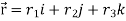

So that

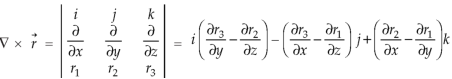
Now-

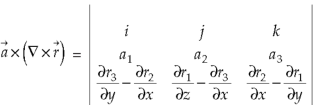
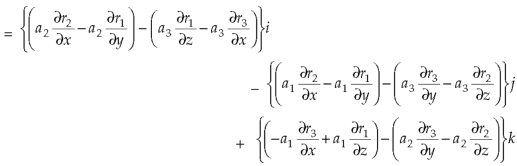
So that-

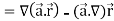
Example-4: Find the curl of F(x,y,z) = 3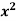i+2zj-xk

Ans.

Curl F =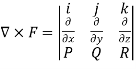

=

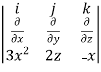
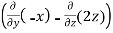= i -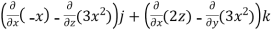

= (0-2)i-(-1-0)j+(0-0)k

= -2i+j

Example-5: What is the curl of the vector field F= ( x +y +z ,x-y-z,)?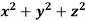

Solution:

Curl F =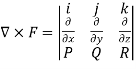

=

=

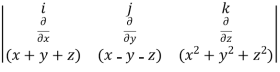
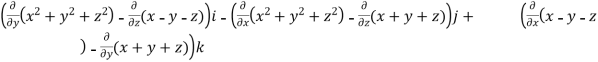
= (2y+1)i-(2x-1)j+(1-1)k

= (2y+1)i+(1-2x)j+0k

= (2y+1, 1-2x,0)

Example-6: Find the curl of F = (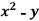)i +4zj +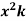

Solution:

Curl F=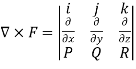

=

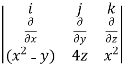
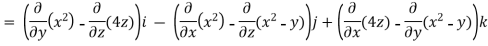
=(0-4)i-(2x-0)j+(0+1)k

=(-4)i – (2x)j+1k

=(-4,-2x,1)

Solenoidal field-

Ansolenoidal field F is characterised by the following conditions-

1.

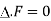
2. Flux 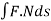along every closed surface is zero.

3.

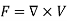
Note- In an solenoidal field for which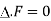 , the vector F can always be expressed as the curl of a vector function V.

So that-

2.4.Irrotational vector field

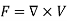
Irrotational field-

An irrotatonal field F is characterised by the following conditions-

1.

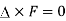
2. Circulation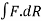 along every closed surface is zero.

3.

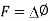
Note- In an irrotational field for which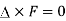 , the vector F can always be expressed as the gradient of a scalar function 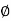provided the domain is simply connected.

So that-

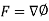
Here the scalar function is called the potential.

Example-1: Prove that the vector field is irrotational and find its scalar potential.

Sol. As we know that if 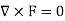then field is irrotational.

So that-

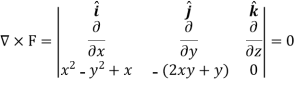
So that the field is irrotational and the vector F can be expressed as the gradient of a scalar potential,

That means-

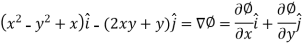
Now-

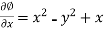   ………………… (1)

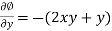  ……………………. (2)

Integrating (1) with respect to x, keep ‘y’ as constant-

We get-

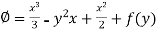      …………….. (3)

Integrating (1) with respect to y, keep ‘x’ as constant-

We get-

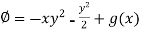      …………….. (4)

Equating (3) and (4)-

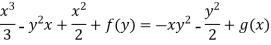
and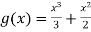

So that-

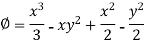
Example-2:Prove that the vector field 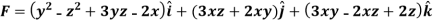is solenoidal and irrotational.

Sol. We know that if 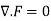 then the vector field will be solenoidal.

So that-

=

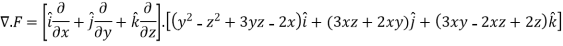
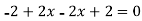
So that the vector field is solenoidal.

Now for irrotational field we need prove-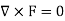 

So that-

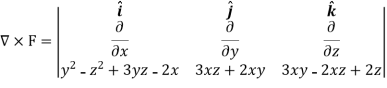
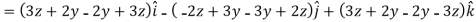
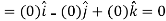
Thus, the vector field F is irrotational.

Example-3:Show that the vector field 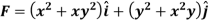is irrotational and find the scalar potential function.

Sol. Now for irrotational field we need prove-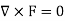 

So that-

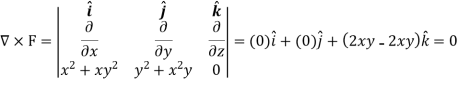
So that the vector field is irrotational.

Now in order to find the scalar potential function-