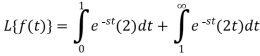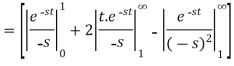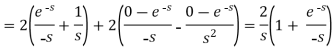UNIT–4

Laplace Transform

4.1. Definition and transform of elementary functions

Let f(t) be any function of t defined for all positive values of t. Then the Laplace transform of the function f(t) is defined as-

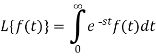
Provided that the integral exists, here ‘s’ is the parameter which could be real or complex.

The inverse of the Laplace transform can be defined as below-

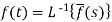
Here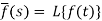

f(t) is called the inverse Laplace transform of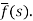

L is called the Laplace transformation operator.

Conditions for the existence of Laplace transforms-

The Laplace transform of f(t) exists for s>a, if

1. f(t) is a continuous function.

2. 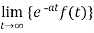is finite.

Important formulae-

1.

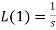
2.

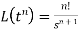
3.

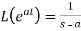
4.

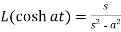
5.

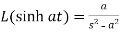
6.

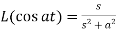
7.

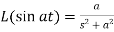
Example-1: Find the Laplace transform of the following functions-

1. 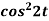                           2.

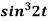
Sol. 1.

Here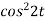

So that we can write it as-

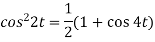
Now-

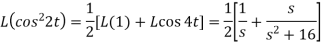
2.  Since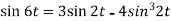 

Or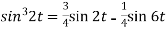            

Now-

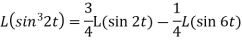
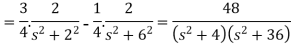
Example-2: Find the Laplace transform of (1 + cos 2t)

Sol.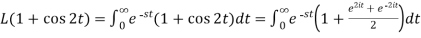

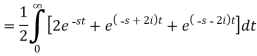
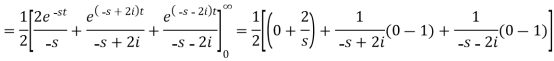
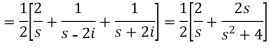
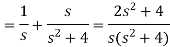
So that-

4.2. Properties of Laplace transform

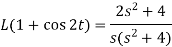
1. Linearity property-

Let a and b be any two constants and 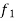, 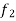any two functions of t, then-

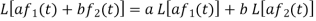
Proof: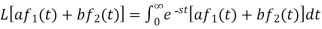

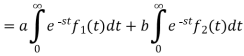
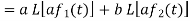
Hence proved.

2. First shifting property (Theorem)- If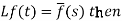

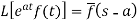
Proof: By definition-

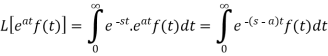
Let (s – a) = r

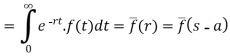
Hence proved.

We can find the following results with the help of the above theorem-

1.

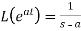
2.

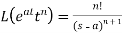
4.

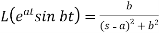
5.

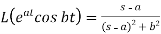
6.

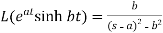
7.

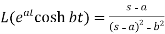
Here s>a in each case.

Example-1: Find the Laplace transform of t sin at.

Sol. Here-

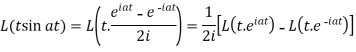
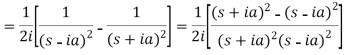
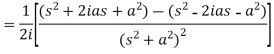
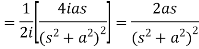
Example-2: Find the Laplace transform of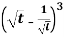

Sol. Here-

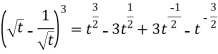
So that-

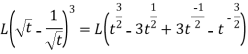
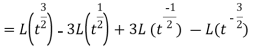
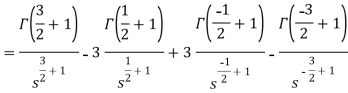
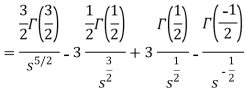
As we know that-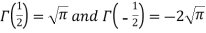  

So that-

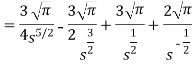
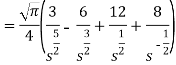
Hence-

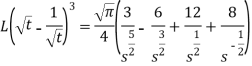
Example-3: Find the Laplace transform of the following function-

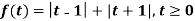
Sol. The given function f(t) can be written as-

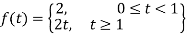
So that, by definition,