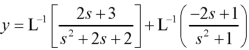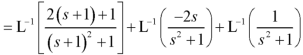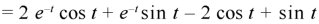UNIT–5
Inverse Laplace Transform
Inverse Laplace transforms-
The inverse of the Laplace transform can be defined as below-
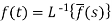
Here 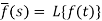
f(t) is called the inverse Laplace transform of 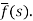
L is called the Laplace transformation operator.
Important formulae-
1. 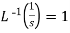 2.
2. 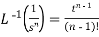
3. 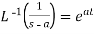 4.
4. 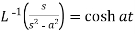
5. 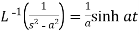 6.
6. 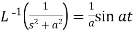
7. 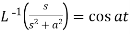 8.
8. 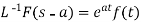
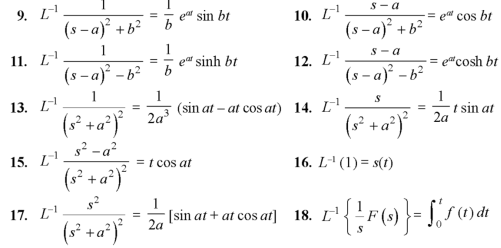
Example: Find the inverse Laplace transform of the following functions-
1. 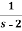
2. 
Sol.
1.
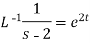
2.
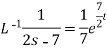
Example: Find the inverse Laplace transform of-
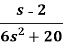
Sol.

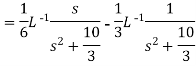
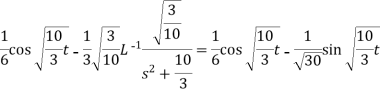
Multiplication by ‘s’ -

Example: Find the inverse Laplace transform of-
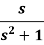
Sol.

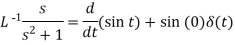
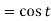
Division by s-
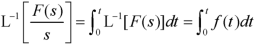
Example: Find the inverse Laplace transform of-
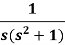
Sol.
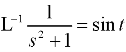

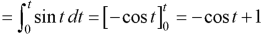
Inverse Laplace transform of derivative-

Example: Find 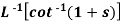
Sol.
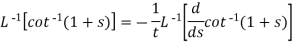
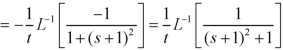
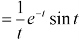
We can find the inverse Laplace transform by using partial fractions method described below-
Example: Find the Laplace inverse of-
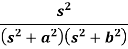
Sol.
We will convert the function into partial fractions-
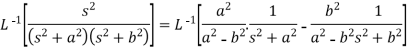

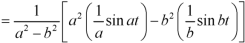
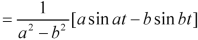
Example: Find the inverse transform of-
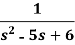
Sol.
First we will convert it into partial fractions-
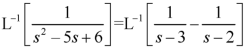

Inverse Laplace transform by convolution theorem-
According to the convolution theorem-

Example: Find
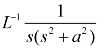
Sol.
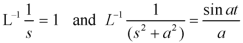
Therefore by the convolution theorem-
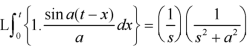
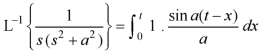
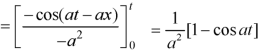
We can solve the linear differential equations with constant coefficients without finding general solution and arbitrary constant, by using Laplace transform.
Example: Solve the following initial value problem by using convolution-
y’’ + y = sin 3t
y(0) = 0, y’(0) = 0
Sol.
y’’ + y = sin 3t
Taking Laplace transform of both sides, we have-
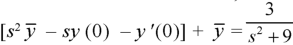
On putting the given values, we get-

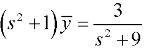
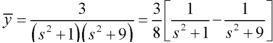
On taking the inverse transformation, we get-
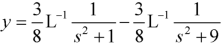
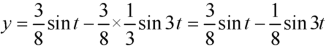
Example: Solve the following initial value problem by using Laplace transform-
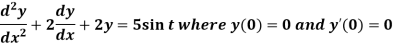
Sol.
We can write this equation as-
y’’+2y’+2y = 5 sin t
Taking the Laplace transformation of both sides, we have-
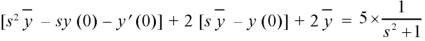
Putting the given values, we get-
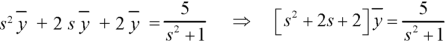
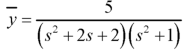
Resolving into partial fractions-
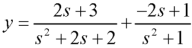
On taking inverse transform, we get-