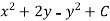UNIT–6

Complex variable

6.1. Function of complex variable

In the narrow sense of the term, the theory of function of a complex variable is the theory of analytic functions (cf. Analytic function) of one or several complex variables. As an independent discipline, the theory of functions of a complex variable took shape in about the middle of the 19th century as the theory of analytic functions.

Complex function-

x + iy is a complex variable which is denoted by z

If for each value of the complex variable z = x + iy in a region R, we have one or more than one values of w = u + iv, then w is called a complex function of z.

And it is denoted as-

w = u(x , y) + iv(x , y) = f(z)

Neighbourhood of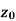

Let a point 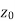in the complex plane and z be any positive number, then the set of points z such that-

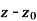||<ε

Is called ε- neighbourhood of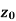

Limit of a function of a complex variable-

Suppose f(z) is a single valued function defined at all points in some neighbourhood of point -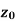

The-

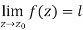
Example-1: Find-

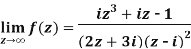
Sol. Here we have-

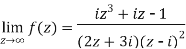
Divide numerator and denominator by 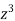, we get-

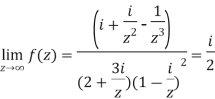
Continuity- A function w = f(z) is said to be continuous at z = 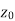, if

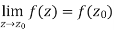
Also if w = f(z) = u(x , y) + iv(x , y) is continuous at z = 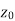then u(x , y), v(x , y) are also continuous at z = .

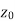Differentiability-

Let f(z) be a single valued function of the variable z, then

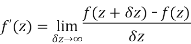
Provided that the limit exists and has the same value for all the different ways in which 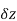approaches to zero.

Example-2: if f(z) is a complex function given below, then discuss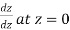

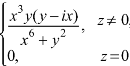
Sol. If z→0 along radius vector y = mx

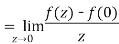
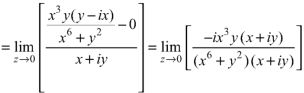
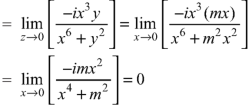
But along ,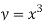

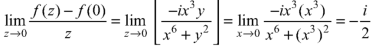
In different paths we get different value of 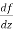that means 0 and –i/2, in that case the function is not differentiable at z = 0.

6.2. Analytic function

A function 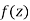is said to be analytic at a point 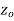if f is differentiable not only at 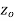but an every point of some neighborhood at .

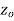Note-

1. A point at which the function is not differentiable is called singular point.

2. A function which is analytic everywhere is called an entire function.

3. An entire function is always analytic, differentiable and continuous function.( converse is not true)

4. Analytic function is always differentiable and continuous but converse is not true.

5. A differentiable function is always continuous but converse is not true.

The necessary condition for f(z) to be analytic-

f(z) = u + i(v) is to be analytic at all the points in a region R are-

1. 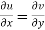       …………. (1)

2. 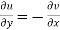   ……...…. (2)

Provided 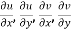 exists

Equation (1) and (2) are known as Cauchy-Riemann equations.

The sufficient condition for f(z) to be analytic-

f(z) = u + i(v) is to be analytic at all the points in a region R are-

1. 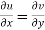       …………. (1)

2. 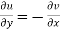   ……...…. (2)

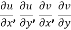are continuous function of x and y in region R.

Important note-

1. If a function is analytic in a domain D, then u and v will satisfy Cauchy-Riemann conditions.

2. C-R conditions are necessary but not sufficient for analytic function.

3. C-R conditions are sufficient if the partial derivative are continuous.

State and prove sufficient condition for analytic functions

Statement – The sufficient condition for a function 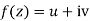to be analytic at all points in a region R are

1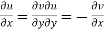       

2 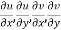           are continuous function of x and y in region R.

Proof :-  Let f(z) be a simple valued function having 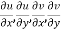     at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem

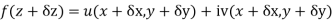
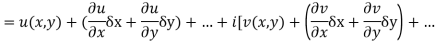
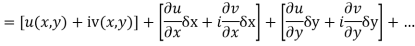
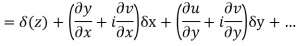
Ignoring the terms of second power and higher power

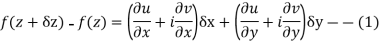
We know C-R equation

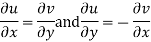
Replacing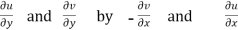

Respectively in (1) we get

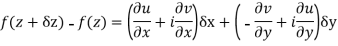
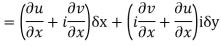
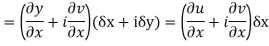
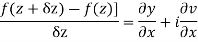
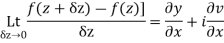
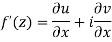
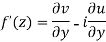
Show that 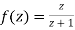is analytic at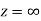

Ans   The function f(z) is analytic at 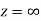if the function 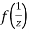is analytic at z=0

Since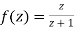

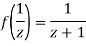
Now 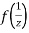is differentiable at z=0 and at all points in its neighbourhood Hence the function 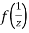is analytic at z=0 and in turn f(z) is analytic at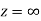

Example-1: If w = log z, then find 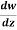. Also determine where w is non-analytic.

Sol. Here we have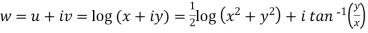

Therefore-

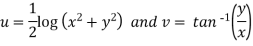
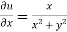and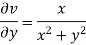
 

Again-

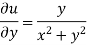
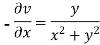
Hence the C-R conditions are satisfied also the partial derivatives are continuous except at (0 , 0).

So that w is analytic everywhere but not at z = 0

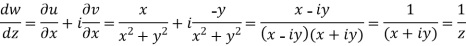
Example-2: Prove that the function 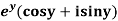is an analytical function.

Sol. Let 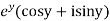=u+iv

Let 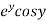=u and 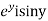=v

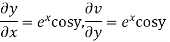
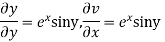
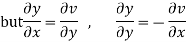
Hence C-R-Equation satisfied.

Example-3: Prove that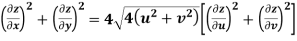

Sol. Given that

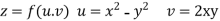
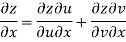
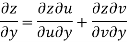
Since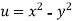      

V=2xy

Now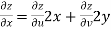

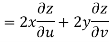
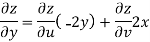
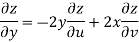
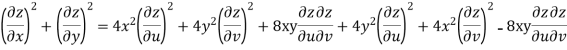
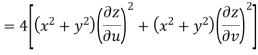
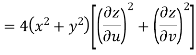
But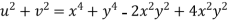                                      

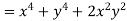
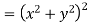
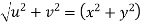
Hence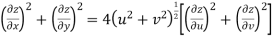 

Example-4: Show that polar form of C-R equations are-

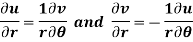
Sol.             z = x + iy =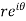

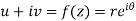
U and v are expressed in terms of r and θ.

Differentiate it partially w.r.t. r and θ, we get-

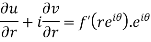
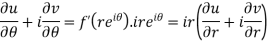
By equating real and imaginary parts, we get-

6.3. Necessary and sufficient condition for f(z) to be analytic

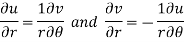
Necessary condition for function f(z) to be analytic-

Theorem; The necessary condition for a function 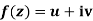to be analytic at all the points in a region R are

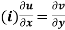         (ii)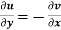

Provided,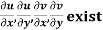

Proof:

Let 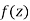be an analytic function in region R.

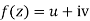
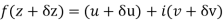
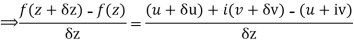
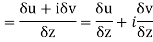
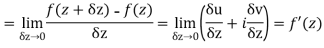
Along real axis

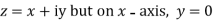
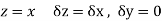
Then f’(z), becomes-

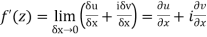      ………… (1)

Along imaginary axis

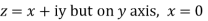
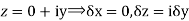
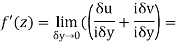
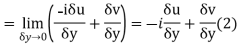
From equation (1) and (2)

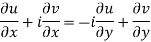
Equating real and imaginary parts

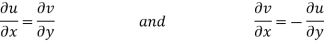
Therefore-

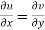and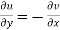

These are called Cauchy Riemann Equations.

Sufficient condition for function f(z) to be analytic-

Theorem-

The sufficient conditions of a function f(z) = u + iv to be analytic at all the points in the region R are-

1.

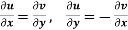
2. 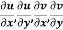are continuous functions of x and y in region R.

Proof:

Suppose f(z) be a single-valued function which has-

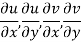
At each point in the R region, then the Cauchy-Reimann equations are satisfied.

By Taylor’s theorem-

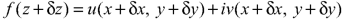
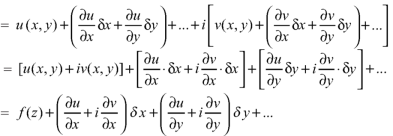
Ignore the terms of higher power.

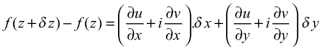
We know that from C-R equations-

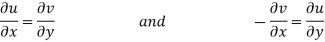
Replace 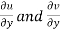by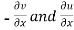

We get-

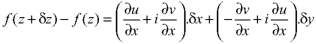
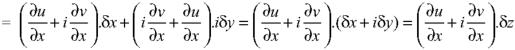
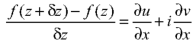
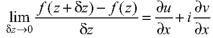
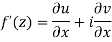
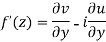
Proved

6.4. Cauchy-Riemann equation in Cartesian and polar coordinates

In Cartesian form-

Theorem; The necessary condition for a function 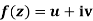to be analytic at all the points in a region R are

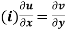         (ii)

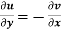
Provided,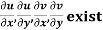

Proof:

Let 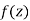be an analytic function in region R.

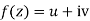
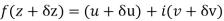
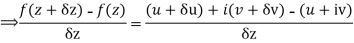
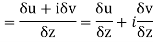
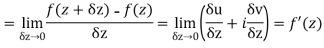
Along real axis

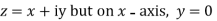
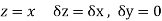
Then f’(z), becomes-

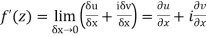      ………… (1)

Along imaginary axis

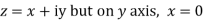
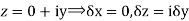
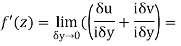
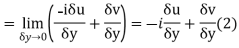
From equation (1) and (2)

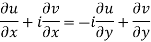
Equating real and imaginary parts

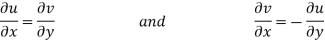
Therefore-

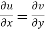and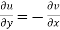

These are called Cauchy Riemann Equations.

C-R equation in polar from-

C-R equations in polar form are-

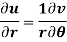
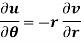
Proof:

As we know that-

x = r cos and u is the function of x and y

z = x + iy = r ( cos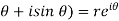

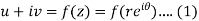
Differentiate (1) partially with respect to r, we get-

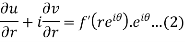
Now differentiate (1) with respect to 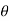, we get-

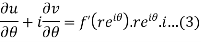
Substitute the value of 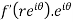, we get-

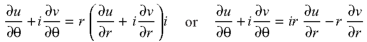
Equating real and imaginary parts, we get-

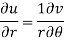
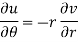
Proved

6.5. Milne-Thomson theorem

Milne-Thomson method is used to construct an analytic function without finding v,

The method is given below-

Since,

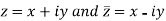
So that-

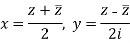
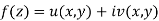
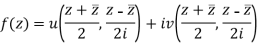
The relation above can be regarded as a formal identity in two independent variables z and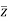

Replacing 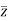by z we get-

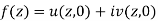
Condition-1 if u is given-

We have-

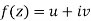
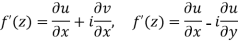
If we write-

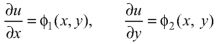
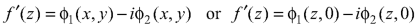
On integrating-

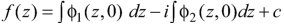
Condition-2: If v is given-

f(z) = u + iv

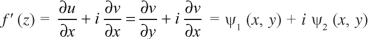
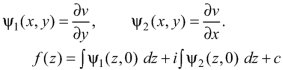
Example: If

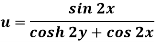
Then find f(z)

Sol.

Here-

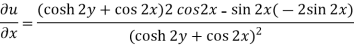
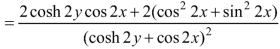
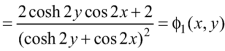
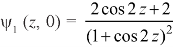
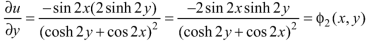
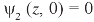
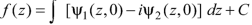
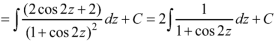
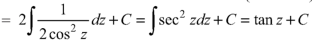
Which is the required answer.

6.6 Harmonic function

A function which satisfies the Laplace equation is known as a harmonic function.

Theorem- if f(z) = u + iv is an analytic function, then u and v are both harmonic functions.

Proof:

Suppose f(z) = u + iv, be an analytic function, then we have 

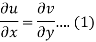
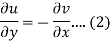
Differentiate (1) with respect to x, we get

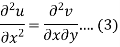
Differentiate (2) with respect to y, we get

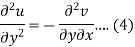
Add 3 and 4-

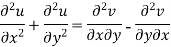
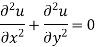
Similarly-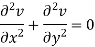
 

So that u and v are harmonic functions.

Example: Prove that 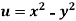and 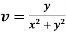are harmonic functions of (x, y).

Sol.

We have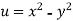

Now

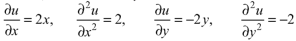
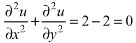
Here it satisfies Laplace equation so that u (x, y) is harmonic.

Now-

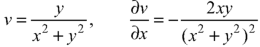
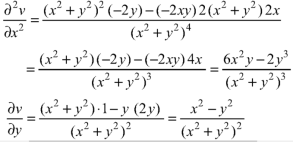
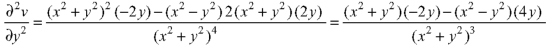
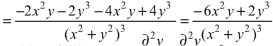
On adding the above results-

We get-

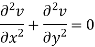
So that v(x, y) is also a harmonic function.

Example: Find the harmonic conjugate function of the function U (x, y) = 2x (1 – y).

Sol.

We have,

U(x, y) = 2x (1 – y)

Let V is the harmonic conjugate of U.

So that by total differentiation,

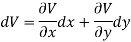
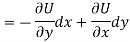
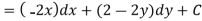
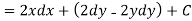
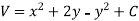
Hence the harmonic conjugate of U is