Unit -1
Properties of Fluids & Dimensional Analysis
A fluid may be defined as follows :
“A fluid is a substance which is capable of flowing.”
Fluid Mechanics :-
Fluid Mechanics may be defined as that branch of engineering Science which deals with the behavior of fluid under the conditions of rest and motion. The fluid mechanics may be divided into three parts: Statics, Kinematics and dynamics.
Statics: The study of incompressible fluids under static conditions is called hydrostatics and that dealing with the compressible static gases is termed as aerostatics.
Kinematics: It deals with the velocities, accelerations and the patterns of flow only. Forcesor energy causing velocity and acceleration are not dealt under this heading.
Dynamics:It deals with the relations between velocities accelerations of fluids with the forces or energy causing them.
Density or Mass Density :
Density or mass density of a fluid is defined as the ratio of the mass of a fluid to its volume.
It is denoted by the symbol (rho).
The unit of mass density in SI unit is kg/m3.
= Mass of fluid / Volume of fluid = m/v
The value of density of water is 1000 kg/m3
Specific weight or weight density
Specific weight or weight density of a fluid is the ratio between the weight of a fluid to its volume.
It is denoted by the symbol w.
w = Weight of fluid / Volume of fluid= W/v
= x g
The value of specific weight or weight density(w) for water is 9810N/m3.
Specific Volume:
Specific Volume of a fluid is defined as the volume of a fluid occupied by a unit mass or volume per unit mass of a fluid is called specific volume.
Mathematically, it is expressed as,
Specific Volume = Volume Of Fluid / Mass of Fluid= v/m
= 1/
It is expressed as m3 /kg.
Relative density or Specific Gravity :
Specific Gravity is defined as the ratio of the weight density of a fluid to the weight density of standard fluid.
Specific gravity is also called relative density. It is dimensionless gravity and is denoted by the symbol S.
S (For Liquids ) = Weight density(density) of liquid / Weight density(density) of
Water.
The specific gravity of mercury is 13.6 and specific gravity of water is 1.
This law states that the shear stress () on a fluid element layer is directly proportional to the rate of shear strain. The constant of proportionality is called the co-efficient of viscosity.
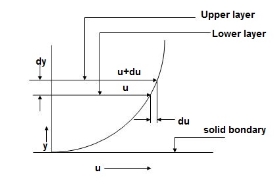
= du / dy
The fluids which follow this law are known as Newtonian fluids
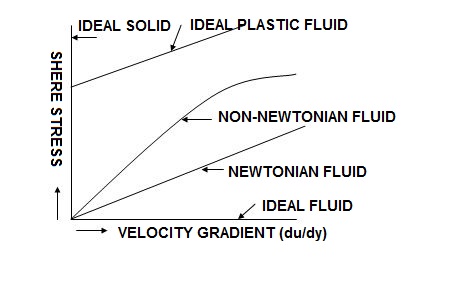
Ideal Fluid :A fluid which is incompressible and is having no viscosity, is known as an ideal fluid. Ideal Fluid is only an imaginary fluids as all the fluids. Which exist have some viscosity.
Real Fluid: A fluid, which possesses viscosity, is known as real fluid. All the fluids in actual practice are real fluids.
Newtonian Fluid: A real fluid, in which the shears stress is directly proportional to the rate of shear strain is known as a Newtonian fluid.
Eg.Water, Kerosine.
Non - Newtonian Fluid: A real fluid, in which the shear stress is not proportional to the rate of shearstainKnown as a Non – Newtonian Fluid.
Example Blood, mud.
Ideal Plastic Fluid : A fluid, in which shares stress is more than the yield value and shear stress is proportional to the rate of shear strain is known as ideal plastic fluid.
Rheological Diagram
Viscosity may be defined as the property of fluid which determines its resistance to shearing stresses. It is a measure of the internal fluid friction which causes resistance to flow.
Viscosity of fluids is due to cohesion and interaction between particles.
du/dy
= du/dy
= Constant of proportionality and is known as co-efficiency of dynamic viscosity.
Du/dy = Rate of shear stress or rate of shear deformation or velocity gradient.
We have,
= / [du/dy]
Thus viscosity may also be defined as the shear stress required to produce unit rate of shear strain.
Unitsof Viscosity:
In S.I.units : N.s/m2
Kinematic Viscosity :
Kinematic Viscosity is defined as the ratio between the dynamic viscosity and density of fluid. It is denoted by v (called nu).
v = Viscosity / Density
= /
Unitsof Kinematic Viscosity :
In SIunits : m2/s
Compressibility The property by virtue of which fluids undergo a change in volume under the action external pressure is known as compressibility.It decreases with the increase in pressure of fluid.
Bulk modulus of elasticity (K) is defined as the ratio of compressive stress to volumetric strain. Compressibility is the reciprocal of bulk modules of elasticity.
Cohesion: Cohesion means intermolecular attraction between molecules of same liquid. It enable a liquid to resist small amount of tensile stresses. Cohesion is a tendency of the liquid to remain as one assemblage of particles.
Adhesion : Adhesion means attraction between the molecule of a liquid and the molecule of a solid boundary surface is contact with the liquid. This property enable a liquid to stick to another body.
Surface tension is caused by the force of cohesion at the free surface.
A liquid molecules in the interior of the liquid mass is surrounded by the other molecules all around and is inequilibrium.
At the free surface of the liquid, there are no liquid molecules above the surface to balance the force of the molecules below it.
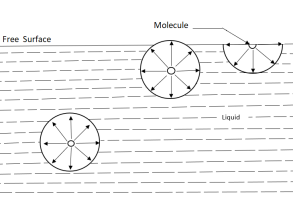
Consequently, as shown in fig there is net inward force on the molecules at the free surface.
The force is normal to the liquid surface.
At the free surface a thin layer of molecules is formed.
It is denoted by letter .
It’s SI unit is N/m.
Capillarity is defined as a phenomenon of rise or fall of a liquid surface in small tube relative to the adjacent general level of liquid when the tube is held vertically in the liquid.
The rise of liquid surface is known as capillary rise while the fall of the liquid surface is known as capillary depression.
It is expressed in terms of cm or mm of liquid.
Its value depends upon the specific weight of the liquid, diameter of the tube and surface tension of the liquid.
h =Height of the liquid in the tube.
d = Diameter of tube
= Surface tension of liquid.
= Angle of contact between liquid and glass tube.
= Density Of liquid.
h= 4cos / e*g*d
All liquid has a tendency to evaporate a vaporize.
Molecules are continuously projected from the free surface to the atmosphere.
These ejected molecules are in a gaseous state and exact their own partial vapor pressure on the liquid surface. This pressure is known as the vapors pressure of the liquid(Pv).
Vapors pressure increase with the rise in temperature.
- The various physical quantities used in fluid phenomenon can be expressed in terms of fundamental quantities or primary quantities.
- The fundamental quantities are mass, length, time and temperature designated by the letters, M, L, T, Ө respectively.
- Th quantities which are expressed in terms of the fundamental or primary quantities are called derived or secondary quantities e.g., velocity, area, acceleration, etc.
- The expression for a derived quantity in terms of primary quantities is called the dimension of the physical quantity.
- A physical equation is the relationship between two or more physical quantities.
- Any correct equation expressing a physical relationship between quantities must be dimensionally homogeneous and numerically equivalent.
- Dimensional homogeneity states that every term in an equation when reduced to fundamental dimensions must contain identical powers of each dimension.
- A dimensionally homogeneous equation is applicable to all system of units.
- In a dimensionally homogeneous equation, only quantities having the same dimensions can be added, subtracted or equated.
P = w h
Dimensions of LHS = ML-1T-2
Dimensions of RHS = ML-2T-2×L = ML-1T-2
Dimensions of LHS = Dimensions of RHS
Hence, equation P= w h is dimensionally homogeneous; so it can be used in any system of units.
Applications of Dimensional Homogeneity:
- It facilitates to determine the dimensions of a physical quantity.
- It helps to check whether an equation of a physical phenomenon is dimensionally homogeneous or not.
- It facilitates conversion of units from one system to another.
- When a large number of physical variables are involved Rayleigh’s method of dimensional analysis becomes increasingly laborious and cumbersome.
- Buckingham’s method is an improvement over the Rayleigh’s method.
- Buckingham’s designated the dimensionless group by the letter Π. It is therefore often called Buckingham Π-Method.
- The Buckingham’s Π-Method states as follows:
“If there are n variables in a dimensionally homogeneous equation and if these variables contain fundamental dimensions (such as M, L, T, etc.) then the variables are arranged into (n-m) dimensionless terms.
- These dimensionless terms are called Π– terms.”
Mathematically, if any variable X1, depends on independent variables, X2, X3, X4,…… Xn; the functional equation may be written as
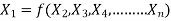-------- 1
Equation 1 can also be written as
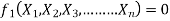-------- 2
It is dimensionally homogeneous equation and contain n variables.
If there are m fundamental dimensions, then according to Buckingham’s Π – theorem, it [eqn] can be written in terms of number of Π – terms in which number of Π terms is equal to (n-m).
Hence equation 2 becomes as
--------3
Each dimensionless 
– term is formed by combining m variables out of the total n variables with one of the remaining (n-m) variable.
These m variables which appear repeated in each of 
– terms are consequently called repeating variables and are chosen from among the variables such that they together involve all the fundamental dimentions and they themselves do not form a dimensionless parameter.
Let in the above case X2, X3 and X4 are the repeating variables if the fundamental dimensions m(M, L, T) = 3, then each term is written as:
.
.
.
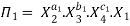
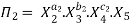
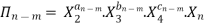-------- 4
Where a1, b1, c1, a2, b2, c2 etc. are the constants, which are determined by considering dimensional homogeneity. These values are substituted in equation 4 and values of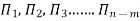 
are obtained. These values of Π’s are substituted in equation 3.
The final general equation for the phenomenon may then be obtained by expressing anyone of the Π – terms as a function of the other as:
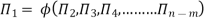
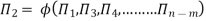
Geometric Similarity:
For geometric similarity to exist between the model and the prototype, the ratios of corresponding lengths in the model and the prototype must be same and the included angles between the corresponding sides must be the same.
Models which are not geometrically similar are known as geometrically distorted model.
Lm = length of model
Hm = height of model
Dm = diameter of model
Am = area of model
Vm = volume of model
And LP, BP, HP, DP, AP and VP = corresponding values of prototype.
Then, for geometric similarity, we must have the relation:
Where Lr is called the scale ratio or the scale factor:
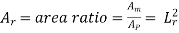
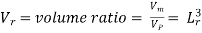
Kinematic similarity:
Kinematic similarity is the similarity of motion.
If at the corresponding points in the model and in the prototype, the velocity or acceleration ratio are same & velocity or acceleration vectors point in the same direction, the two flows are said to be kinematically similar.
(V1)m = velocity of fluid at point 1 in the model.
(V2)m = velocity of fluid at point 2 in the model,
(a1)m = acceleration of fluid at point 1 in the model
(a2)m = acceleration of fluid at point 2 in the model
And (V1)P, (V2)P, (a1)P (a2)P = corresponding values at the corresponding points of fluid, velocity and acceleration in the prototype.
Then, for kinematic similarity, we must have
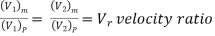
Similarly,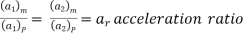 
The direction of the velocities in the model and prototype should be same.
The geometric similarity is a pre-requisite for kinematic similarity.
Dynamic Similarity
Dynamic similarity is the similarity of forces. The flows in the model and in prototype are dynamically similar if at all the corresponding points, identical types of forces are parallel and bear the same ratio.
In dynamic similarity, the force polygons of the two flows can be superimposed by change in force scale.
(Fi)m = inertia force at apoint in the model,
(Fv)m = viscous force at the point in the model,
(Fg)m = gravity force at the point in the model
And (Fi)P, (Fv)P, (Fg)P = corresponding values of forces at the corresponding points in prototype.
Then, for dynamic similarity we have
The direction of the corresponding forces at the corresponding points in the model and prototype should also be same.
Reynold’s Number (Re)
It is defined as the ratio of the inertia force to the viscous force.
Reynold’s Number, Re = 
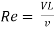
For pipe flow (where the linear dimension is taken as diameter d),
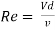
Reynold’s number signifies the relative predominance of the inertia to the viscous forces occurring in the flow systems.
Fraud’s Number (Fr)
It is defined as the square root of the ratio of the inertia force and the gravity force.
Mathematically, 
Froude number governs the dynamics similarity of the flow situations; where gravitational force is more significant and all other forces are comparatively negligible.
Euler’s Number (Eu)
It is defined as the square root of the ratio of the inertia force to the pressure force.
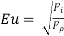
The Euler number is important in the flow problems / situations in which a pressure gradient exists.
Weber’s Number (We)
It is defined as the square root of the ratio of the inertia force to the surface tension force.
Mathematically,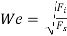 
This number assumes importance in the following flow situation:
i) Flow of blood in veins and arteries
Ii) Liquid atomisation, and
Iii) Capillary movement of water in soils
Mach Formula (M)
It is defined as the square root of the ratio of the inertia force to the elastic force.
Mathematically,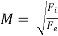 
The Mach number is important in compressible flow problems at high velocities, such as high velocity flow in pipes or motion of high speed projectiles and missiles.
To ensure dynamic similarity between the model and prototype it is necessary that the ratio of the corresponding forces acting at the corresponding points in the model and prototype be made equal.
It implies that dimensionless numbers should be same for the model as well as the prototype.
This condition is difficult to be satisfied for all the dimensionless numbers.
Hence models are designed on the basis of the force which is dominating in the flow situation. The laws on which the models are designed for dynamic similarity are called model or similarity laws; these are
Reynolds Model Law
In flow situations where in addition to inertia, viscous force is the other predominant force, the similarity of flow in the model and its prototype can be established if Reynolds number is same for both the systems.
This is known as Reynolds law and according to this law,
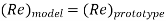
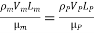
Where, ρm = density of fluid in model
Vm = velocity of fluid in model,
Lm = length of linear dimension of the model, and
µm = viscosity of fluid in model
And ρP, VP, LP and µP are the corresponding values of density, velocity, linear dimension and viscosity of fluid in prototype.
Or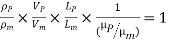 
Or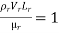 
[ 
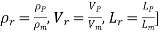
Following are some of the phenomenon for which Reynolds model law can be a sufficient criterion for similarity of flow in the model and the prototype:
- Motion of air planes,
- Flow of incompressible fluid in closed pipes,
- Motion of submarines completely under water, and
- Flow around structures and other bodies immersed completely under moving fluids.
Froude Model Law
When the gravitational force can be considered to be the only predominant force which controls the motion in addition to the inertia force, the similarity of the flow in any two such systems can be established if the Froude’s number of both the systems is the same.
This is known as Froude’s Model Law.
Some of the phenomenon for which the Froude Model Law can be sufficient criterion for dynamic similarity to be established in the model and the prototype are:
- Free surface flows such as flow over spillways, sluices, etc.
- Flow of jet from an office or nozzle;
- Where waves are likely to be formed on the surface;
- Where fluids of different mass densities flow over one another
Let, Vm = velocity of fluid in model
Lm = length (or linear dimension) of the model
gm = acceleration due to gravity (at a place where model is tested)
And VP, LP and gP are the corresponding values of the velocity, length and acceleration due to gravity for the prototype.
Then according to Froude Law,
(Fr)m = (Fr)P
Or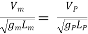 
------ 1
As the value of g at the site of mode testing will be practically the same as at site of the proposed prototype, therefore gm = gP and the equation 1 values as
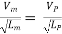
Or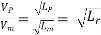 
Where Lr = scale ratio for length
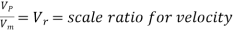
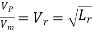
Numericals :
1]. Calculate the specific weight, density & specific gravity of one liter of liquid which weighs 7 N
Given Find
V = 1 lit = 1/1000 = 1 x 10-3 m3,, S
W = 7 N
i). Specific weight = W/V = 7/1 x 10-3 = 7000 N/m3
Ii). Density = /g = 7000/9.81 = 713.5 kg/m3
Iii). Specific gravity S = /w = 7000/9810 = 0.713
2]. The absolute viscosity of liquid having specific gravity of 0.87 is 0.073 poise. Find kinematic viscosity in m2/s & stoke.
Given Find
S = 0.87 v
= 0.073 poise = 0.073/10
= 7.3 x 10-3 Ns/m2
1). Density = S x w
= 0.87 x 1000
= 870 kg/m3
2). Kinematic viscosity = v = / = 7.3 x 10-3 / 870
= 8.39 x 10-6 m2/s
= 8.39 x 10-6/10-4
= 0.0839 stoke
3]. A flat plate of area 1.5 x 106 mm2 is pulled with a speed of 0.4 m/s relative to another plate located at a distance of 0.15 mm from it. Find the force & power required to maintain this speed, if the fluid separating them is having viscosity as 1 poise.
Given Find
A = 1.5 x 106 mm2 = 1.5 m2 F, P
Du = 0.4 m/s
Dy = 0.15 mm = 0.15 x 10-3 m
= 1 poise = 1/10 = 0.1 Ns/m2
1). = du/dy = 0.1 x 0.4/0.15 x 10-3 = 266.67 N/m2
2). F = x A = 266.67 x 1.5 = 400 N
3). Power(P) = F x u
= 400 x 0.4
= 160 watts
4]. Calculate the dynamic viscosity of an oil, which is used for lubrication between a square plate of size 0.8 m x 0.8 m &an inclined plane with angle of inclination 300 as shown in fig. The weight of the square plate is 300 N & it slides down the inclined plane with a uniform velocity of 0.3 m/s. The thickness of oil film is 7.5 mm.
Given
A = 0.8 x 0.8 = 0.64 m2
= 300
W = 300 N
u = 0.3 m/s
Dy = 1.5 mm = 1.5 x 10-3 m
1). F = 300Sin = 300 sin30 = 150 N
2). = F/A = 150/0.64 = 234.375 N/m2
3). = du/dy
xdy/du =
234.375 x 1.5 x 10-3/0.3 =
= 1.17 Ns/m2
5]. The dynamic viscosity of an oil, used for lubrication between a shaft & sleeve is 6 poise. The shaft is of diameter 0.4m & rotates at 190 rpm. Calculate the power lost in the bearings for a sleeve length of 90 mm. The thicknessof the oil film is 1.5 mm.
Given Find
= 6 poise = 6/10 = 0.6 Ns/m2 Power lost
D = 0.4 m
N = 190 rpm
L = 90 mm = 0.09 m
Dy = 1.5 mm = 1.5 x 10-3 m
1). u = πDN/60 = π x 0.4 x 190/60 = 3.98 m/s
2). Du = u-0 = 3.98 m/s
3). = du/dy = 0.6 x 3.98/1.5 x 10-3 = 1592 N/m2
4). F = x Area
= 1592 x π x D x L
= 1592 x π x 0.4 x 0.09
= 180.05 N
5). Torque = F x D/2 = 180.05 x 0.4/2 = 36.01 Nm
6). Power lost = 2πNT/60 = 2π x 190 x 36.01/60 = 716.48 W
6]. Two large plane surfaces are 2.4 cm apart. The space between the surfaces is filled with glycerin. What force is required to drag a very thin plate of surface area as square meter between the two large plane surfaces at a speed of 0.6 m/s if,
i). The thin plate is in the middle of the two plane surfaces.
Ii). The thin plate is at a distance of 0.8 cm from one of the plane surfaces?
Take = 8.10 x 10-1 Ns/m2
Given :
A = 0.5 m2
u = 0.6 m/s
= 8.10 x 10-1 Ns/m2
Case 1.When the thin plate is in the middle of the two planes.
Dy = 0.024/2 = 0.012 m
= du/dy
= 8.10 x 10-1 x 0.6/0.012 = 40.5 N/m2
F = x A x 2
= 40.5 x 0.5 x 2
= 40.5 N
Ii). When the thin plate is at a distance of 0.8 cm from one of the plane.
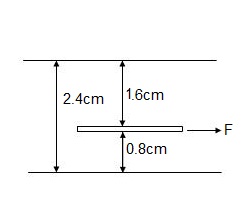
Dy1 = 0.008 m
Dy2 = 0.024 – 0.008 = 0.016 m
1 = du/dy1 = 8.10 x 10-1 x 0.6/0.008
= 60.75 N/m2
F1 = 1 x A = 60.75 x 0.5 = 30.375 N
2 = du/dy2 = 8.10 x 10-1 x 0.6/0.016
= 30.375 N/m2
F2 = 2 x A = 30.375 x 0.5 = 15.187 N
F = F1 + F2
= 30.375 + 15.187
= 45.562 N
7] A vertical gap 2.2 cm wide of infinite extent contains a fluid of viscosity 2 Ns/m2& sp.gr 0.9. A metallic plate 1.2m x 1.2m x 0.2cm is to be lifted up with a constant velocity of 0.15 m/sec, through the gap. If the plate is in the middle of the gap. Find force required.
The weight of the plate is 40N.
Width of gap = 2.2 cm = 0.022 m Find F.
= 2 Ns/m2
S = 0.9
= S x 9810 = 0.9 x 9810
= 8829 N/m3
Size of plate = (1.2 x 1.2 x (2 x 10-3))m
Du = 0.15 m/sec
Weight of plate = 40 N
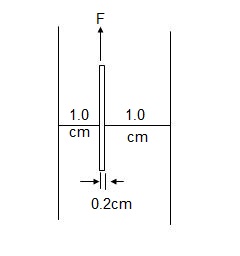
1). Distance of plate from vertical surface of the gap, when plate is in the middle.
Dy = 0.022 – 2 x 10-3/2 = 0.01 m
2). = x du/dy = 2 x 0.15/0.01 = 30 N/m2
3). Total shear force = 2 x x A
F = 2 x 30 x (1.2 x 1.2)
= 86.4 N
4). The upward thrust = weight of fluid displaced
= x v
= 8829 x 1.2 x 1.2 x 2 x 10-3
= 25.43 N
5). Effective weight of= weight ofplate – Upward thrust
The plate
= 40 – 25.43
= 14.57 N
6). Total force required to = F + 14.57
Lift the plate up
= 86.4 + 14.57
= 100.97 N
8] Using Buckingham’s Πtheorem ,show that velocity through circular orifice is given by
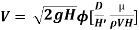
Where H= Head causing flow
D = Diameter of orifice
µ = co-efficient of viscosity
ρ = Density
Solution: V is the function of H, D, µ, ρ, and g
Mathematically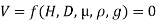 
Or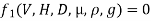 
Total number of variables n = 6
Writing dimensions of each variable
V = LT-1, H = L, D = L, µ = ML-1T-1, ρ = ML-3, g = LT-2
No. Of fundamental dimensions m = 3
No of Π terms = n-m = 6-3 = 3
Each Π term contains (m+1) variables where m=3 and is also equal to repeating variables. Choosing H, g, ρ as repeating variables.
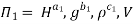
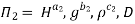
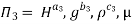
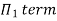
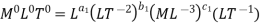
For M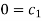 
For L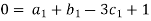 
For T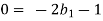 
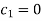and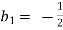 
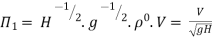
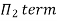
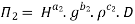
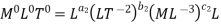
For M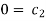 
For L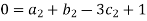 
For T 
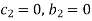
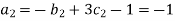
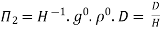
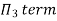
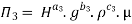
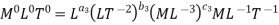
For M 
For L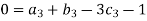 
For T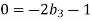 
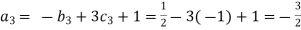
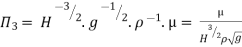
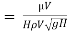
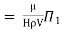
Substituting the values of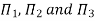 
in equation 1
Or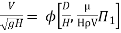 
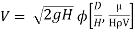
9] The discharge Q of a centrifugal pump depends upon the mass density of fluid (ρ), the speed of the pump (N), the diameter of the impeller D, the manometric head Hm and the viscosity of fluid µ. Show that
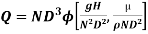
Solution: The discharge Q is function of N, g, D, H, µ, ρ.
Mathematically,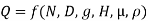 
Or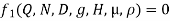 
Total number of variables n = 7
Q = L3T-1, N = T-1, D = L, g = LT-2, H = L, µ = ML-1T-1, ρ = ML-3
No. Of fundamental dimensions m =3
Number of Π terms = n – m = 7 – 3 = 4
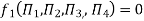-------- 1
Each Π term contains (m+1) variables where m =3 and also equal to repeating variables. Choosing D, N, ρ as repeating variables.
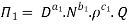
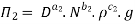
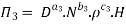
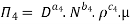
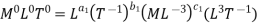
For M 
For L 
For T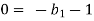 
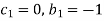
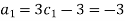
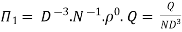
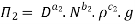
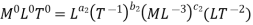
For M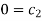 
For L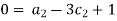 
For T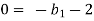 
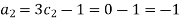
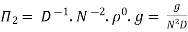
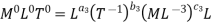
For M 
For L 
For T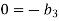 
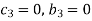
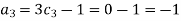
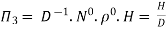
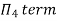
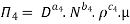
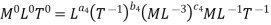
For M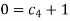 
For L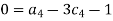 
For T 
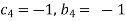
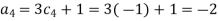
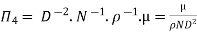
Substituting the values of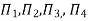 
in equation 1
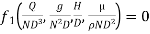
As the product of two Π – terms is also dimensionless, the terms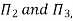 
can be replaced by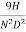 
Or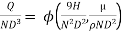 
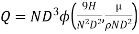
Reference:
Fluid mechanics – R.K. Rajput
Fluid mechanics & hydraulic machines. – R.K. Bansal
