Unit - 4
Fluid Dynamics, Bernoulli’s equation
The motion of the fluid element is influenced by the following forces
- Normal pressure force
The net pressure force in X direction = p dydz –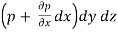 
= 
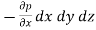
2. Gravity or body force
Let B be the body force per unit mass of fluid having components Bx, By&Bz
In x, y & z directions respectively.
Then, body force acting on the parallelepiped in the direction of X coordinate is = Bx
dx dydz
3. Inertia force
The inertia force acting on the fluid mass, along the X coordinates is given by,
Mass x acceleration = 
dx dydz
Consider steady flow of an ideal fluid along the shown tube.
Separate out a small element of fluid of cross- sectional area dA and length ds from stream tube as a free body from the during fluid.
Fig. Shows such a small elements LM of fluid of cross Section area dA and length ds.
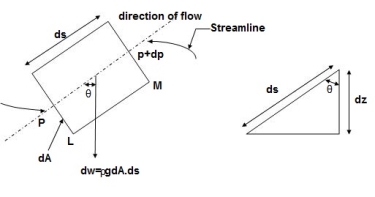
Let, p= Pressure of an the elements at L
p + dp = Pressure on the element at M,and
V=Velocity of the fluid element.
The external forces tending to accelerate the fluid elements in the direction of streamline are as follows:
- Net pressure force in the direction of flows is, p.dA – (p+dp)dA = -dp. DA
- Component of the weight of the fluid elements in the direction of flows is
= -
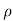.g.dA.ds.cos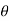
=-
.g.dA.ds (dz/ds) (:. Cos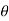
= dz/ds)
= -
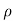.g.dA.dz
Mass flow of the fluid element = 
.dA.ds
The Acceleration of the fluid element
a = dv/dt = dv/ds * ds/dt = v. Dv/ds
Now , according to Newton’s second law of motion, force= mass x acceleration.
:. – dp. DA.-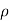
.g.dA.dz= 
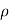.dA.ds x v.dv/ds
Dividing both sides by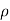 
.dA, we get
-dp/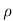
- g.dz= v.dv
Or dp/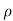
+ v.dv + g.dz=0
This is the required Euler’s equation for motion.
Integrating the Euler’s equation of motion we get
1/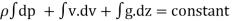
p/
+ v2 /2 + gz = constant
Dividing by g, we get
p/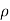
g + v2/2g + z = constant
p/w + v2/2g + z = constant
Or in other words,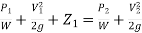 
+
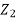
Which proves Bernoulli’s equation.
Assumptions made in Bernoulli’s equation.
- The liquid is ideal & incompressible.
- The flow is steady & continuous.
- The flow is along stream line.
- The velocity is uniform over the section & equal to mean velocity.
- Only forces acting on the fluid are the gravity forces & pressure forces.
- Bernoulli’s equation is derived based on the assumption that fluid is non viscous & therefore frictionless.
- Practically, all fluids are real & therefore viscous & there are always some losses in fluid flows.
- These losses have, therefore, to be taken into account in the application of Bernoulli’s equation which gets modified as follows
+
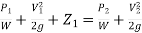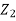+ hL
hL = Loss of energy between section 1 & 2.
Applications of Bernoulli’s equation
Bernoulli’s equation is applied is all problems of incompressible fluid flow where energy considerations are involved, But we shall consider its applications to the following measuring devices:
i) Venturimeter
Ii) Pitot- tube
Iii) Sub-merged orifice
Iv) Orifice meters
v) Rotameter.
Limitation of Bernoulli’s equation
- Velocity of every liquid particle, across any section of pipe is not uniform.
- Bernoulli’s equation is not applicable for fluid with unsteady flow.
- If fluid flowing in a curved path, the energy due to centrifugal force should be taken into account.
The concept of hydraulic gradient line and total energy line is quite useful in the study of flow of fluid in pipes.
Total energy Line (T.E.L. Or E.G.L)
- It is known that the total head with respect to any arbitrary datums, is the sum of the elevation (potential) head, pressure head and velocity head.
Total head =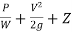 
- When the fluid flows along the pipe, there is loss of head and the total energy decreases in the direction of flow. If the total energy at various point along the axis of the pipe is plotted and joined by a line, the line so obtained is called the Energy gradient line (E.G.L)
- Energy gradient line (E.G.L) is also known as Total energy line (T.E.L)
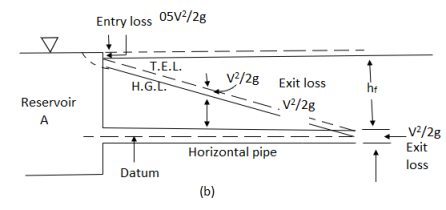
Hydraulic gradient Line (H.G.L)
- The sum of potential head and the pressure head
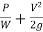at any point is called the piezometric head. - If a line is drawn joining the piezometric levels at various points, the line so obtained is called the ‘Hydraulic gradient line.
- Hydraulic gradient line (H.G.L) is always below the energy gradient line (E.G.L) and the vertical intercept between the two is equal to the velocity head
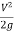
Linear momentum equation
- It is based on law of conservation of momentum or on the momentum principle, which states that the net force acting on a fluid mass is equal to the change in momentum of flow per unit time in that direction.
- The force acting on a fluid mass m is given by the Newtons second law of motion.
F = m x a
Where a is the acceleration acting in the same direction as force F
But a =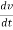 
F = m x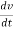 
= 
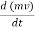m is constant can betaken inside the differential
Above equation is known as the momentum principle.
It can be written as F dt = d(mv)
Which is known as the momentum equation & states that the impulse of force F acting on a fluid of mass m in a short interval of time dt is equal to the change of momentum d(mv) in the direction of force.
Kinetic Energy Correction Factor
Kinetic energy correction factor is defined as the ratio of the kinetic energy of flow per second based on actual velocity across the section to kinetic energy of flow per second based on average velocity across the same section. It is denoted by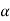 
.
= 
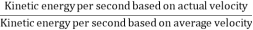
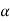= 1 for uniform velocity distribution
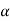= 1.02 to 1.15 for turbulent flows.
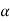= 2 for laminar flow.
Momentum Correction Factor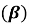
Momentum correction factor is defined as the ratio of momentum of the flow per second based on actual velocity to the momentum of the flow per second based on average velocity across a section. It is denoted by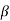 
.
= 
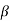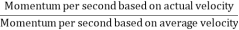
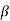= 1 for uniform flow
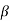= 1.01 to 1.07 for turbulent flow in pipes
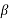= 4/3 = 1.33 for laminar flow in pipes.
A venturimeter is a device used for measuring the rate of a flow of a fluid flowing through a pipe it consists of three parts:
i) A short converging part, ii) Throat, and (iii)Diverging Part
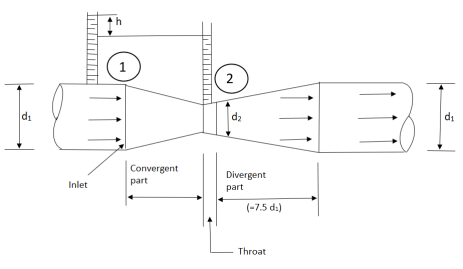
It is based on the principleof Bernoulli’s equation.
Expression for Rate of flow through venturimeter
Consider a venturimeter fitted in a horizontal pipe through which a fluid is following as shown in fig.
Let d1 = diameter at inlet or at section(1)
P1= pressure at section (1)
V1 = velocity of fluid at section (1)
a1= area of section (1) =π/4. d2
And d2, P2, V2, a2 are corresponding values at section (2)
Applying Bernoulli’s equation at section (1) and (2) we get
+
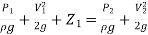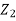
As pipe is horizontal hence z1 = z2
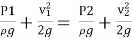
But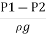 
is the difference of pressure heads at section land 2 and it is equal to h
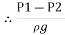=h
Substituting this value of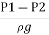 
in the above eqn we get.
h =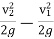 
………….. (1)
Now applying continuity equation at section 1 and 2
a1 v1 = a2 v2
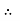v1 =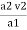 
Substituting this value of v1 in equation 1
= 
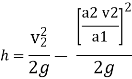
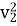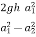
Q = a2v2
=a2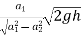 
= 
Above equation gives the discharge underideal conditions and is called,theoretical discharge Actual discharge will be less than theoretical discharge.
Qact =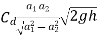
Where Cd = co-efficient of venturimeter and its value is less than 1.
Orifice Meters or Orifice plate.
- It is a device used for measuring the rate of flow of a fluid through a pipe.
- It is a cheaper device compared to venturimeter
- It also works on the same principle as that of venturimeters.
- It consist of a flat circle plate which has a circular shape edged hole called orifice, which is concentric with the pipe.
- The orifice diameters is kept generally 0.5 times the diameters of the pipe, though it may vary from 0.4 to 0.8 time the pipe diameters.
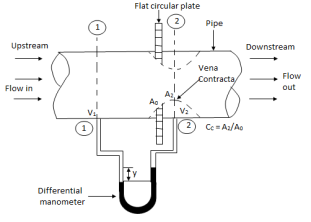
- A differential manometers is connect at section (1),which is at a distance of about 1.5 to 2.0 times the pipe diameters upstream from the orifice plate, and at section (2), which is at a distance of about half the diameters of the orifice on the downstream side from the orifice plate.
Construction-
- It consists of a tapered metering glass tube inside of which is located a rotor or active element (float) of the meter.
- The tube is provided with inlet and outlet connections.
- The specific gravity of the float or Bob material is higher than that of the fluid to be metered.
- On a part of the float spherical slots are cut in which cause itto rotate slowly about the axis of the tube and keep it centered.
- Owing to this spinning accumulation of any sediment on the top or sides of float is checked.
- However, the stability of the bob may also be ensured by using a guide along with the float would slide.
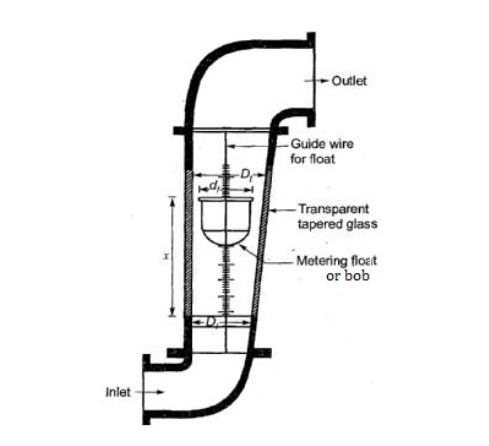
Working-
- When the rate of flow increases, the float rises in the tube and consequently there is an increase in the annular area between the float and the tube.
- Thus, the float rides higher or lower depending on the rate of flow.
The discharge through a rotameter is given by:
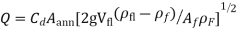
Q = Volume flow rate
Cd = coefficient of discharge.
Aann = Annular area between float and tube
Vfl = Volume of float.
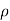fl = Density of float material
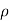f = Density of fluid, and
Af = Maximum cross sectional area of the fluid.
As the flow area Aann is a function of height of float in the tube, the flow rate scale can be engraved on the tube corresponding to a particular float.
Advantages
1) Simpler in operating.
2) Handling and installation is easy.
3) Wide variety of corrosive fluids can be handled.
4) Low cost.
Limitations
1) Mounted vertically, limited to small pipe sizes and capacities.
2) Less accurate compared to Venturimeter and orificemeter.
An orifice is an opening in the wall or base of a vessel through which the fluid flows. The top edge of the orifice is always below the free surface.
Flow through an orifice
- Figure shows a small circular orifice with sharp edge in the side wall of a tank discharging free into the atmosphere.
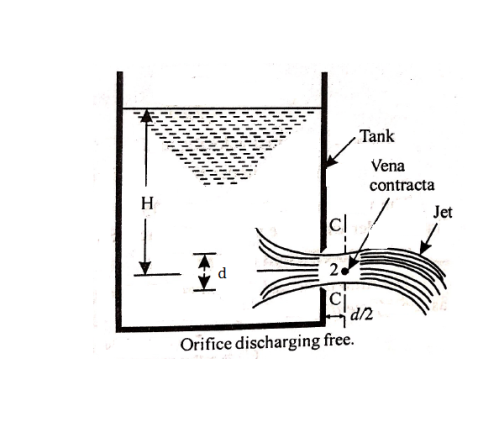
- Let the orifice be at a depth H below the free surface.
- As the fluid flows through the orifice, it contracts and attains a parallel form at a distance d/2 from the plane of the orifice.
- The point at which the streamline first become parallel is termed as Vena contracta.
- Beyond this section, the jet diverges and is attracted in the downward direction by gravity.
Considering points 1 and 2 as shown in figure and applying Bernoulli’s theorem, we have
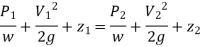
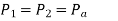
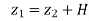
Further, if the cross-sectional area of the tank is very large, the liquid at point 1 is practically standstill and hence V1 = 0
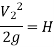
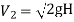
Coefficient of Contraction (Cc)
The ratio of area of the jet at vena contracta to the area of the orifice is known as coefficient of contraction. It is denoted by Cc.
ac= Area of jet at vena contracta, and
a = Area of orifice
Cc = ac/a
The value of Cc varies from 0.613 to 0.69.
Coefficient of velocity (Cv)
The ratio of actual velocity (v) of the jet at vena contracta to the theoretical velocity (Vth)is known as coefficient of velocity.
It is denoted by Cv.
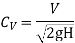
Where, V = Actual velocity
H = Head under which the fluid flows out of the orifice.
The value of Cv varies from 0.95 to 0.99.
Coefficient of Discharge (Cd)
The ratio of actual discharge (Q) through an orifice to the theoretical discharge (Qth) is known as coefficient of discharge.
It is denoted by Cd.
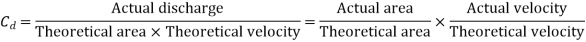
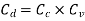
The value of Cd varies from 0.62 to 0.65
Coefficient of Resistance (Cr)
The ratio of loss of head in the orifice to the head of water available at the exit of the orifice is known as coefficient of resistance.
It is denoted by Cr.
- It is a device used for measuring the velocity of flow at any point in a pipe or a channel.
- It is based on the principle, that if the velocity of flow at a point becomes zero, the pressure there is increased due to the conservation of the kinetic energy into pressure energy.
- In its simplest form, the pitot- tube consist of a glass tube, bent at right angles as shown in fig.
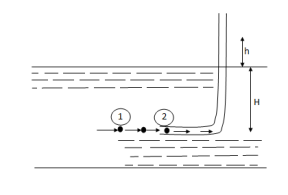
- The Lower end, which is bent though 90° is directed in the upstream direction as shown in fig.
- The liquid rises up in the tube due to the conservation of kinetic energy into pressure energy.
- The velocity is determined by measuring the rise of liquid in the tube.
P1= intensity of pressure at point (1)
V1 = velocity of flow at (1)
P2 = pressure at point (2)
V2 = velocity at point (2), which is zero
H = depth of tube in the liquid.
h = rise of liquid in the tube above the fire Surface
Applying Bernoulli’s equation at points (1) and (2)
We get
+
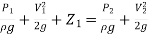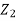
But Z1 = Z2 as points (1) and (2) are an the same line and V2 =0
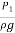= pressure Lead at (1) = H
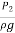= pressure head at (2) = (h+H)
Substituting these values, we get
H+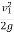 
= (h+H)
:. h=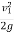 
or V1 =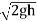 
This is theoretical velocity.
Actual velocity is gives by (V1)act= Cv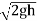
Where Cv= Co-efficient of pitot-tube
:. Velocity at any point V= Cv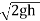
Numerical:
- An oil of sp.gr 0.8 is flowing through a venturimeter having inlet diameter 20 cm & throat diameter 10cm The oil mercury differential nanometers shows a reading 25 cm. Calculate the discharge of oil through the horizontal venturimeter Take cd = 0.98
Given Find Q = ?
S1= 0.8
Sm =13.6
d1=0.2m
d2=0.1m
x=0.25m
Cd=0.98
A1 = π/4*d12 = π/4*0.22 = 0.0314 m2
A2 = π/4*d22= π/4* 0.12 = 7.85*10-3m2
= 4m
Q =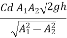 
= 
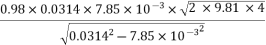
=0.0705 m3/sec
2. The inlet & throat diameters of horizontal venturimeter are 30cm & 10cm respectively. The liquid flowing throat the meter is water,the pressure intensity at inlet is 13.734 N/cm2 while the vacuum pressure head at the throat is 37cm of mercury. Find rate of flow Assume that 4%of the differential head is lost between the inlet & throat. Find also the value Cd for the venturimeter.
Given Find Q
d1 =0.3m Cd
d2= 0.1m
p1=13.734 x104N/m2
Vacuum pressure head = - 0.37m of Hg
hf = 4 % of h = 0.04h
A1=
x d12 =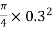
=0.0706m2
A2= 
x d22=
=
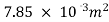
P2 = w *Vacuum pressure head
= (13.6 x 9810) x -0.37
= - 49.37 x103 N/m2
h=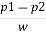 
=
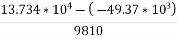
= 19.03 m
hf= 0.04h = 0.04 x 19.032 = 0.7613m
Cd =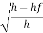 
=
= 0.98
Q=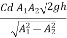
= 
= 0.149 m3/sec
3. A 30cm x 15cm venturimeter is provided a vertical pipe line carrying oil of specific gravity 0.9, The flow being upwards. The different in elevation of the venturimeter is 30cm. The differential U tube mercury manometer shows a gauge deflection of 25cm calculate i) the discharge ii) pressure difference between the entrance section throat section. Take Cd = 0.98
Given Find Q, P1 – P2
d1 = 0.3m
d2 = 0.15m
SL =0.9
Z1=0
Z2 = 0.3 M
X = 0.25 M
A1 = π/4 * d12 = π/4*0.32 = 0.0706m2
A2 = π/4 * d22 = π/4*0.152 = 0.0176m2
h=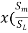
- 1) = 0.25 (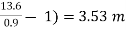
Q =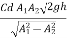
= 
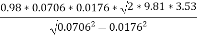
=0.149 m3/sec
h=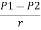 
+(z1-z2)
3.53 = 
+(0 - 0.3)
P1-P2 =33.81 x 103 N/m2
4. Find the discharge of water flowing through a pipe 30cm diameter placed in on inclined position where a venturimeter is inserted, having a throat diameter of 15 cm. The difference of pressure between the main & throat is measured by a sp.gr 0.6 in an inverted tube which gives a reading of 30 cm. The loss of head between the main & threat 0.2 times the kinetic head of the pipe.
Given find Q
d1 = 0.3 m
d2 = 0.15m
Sm = 0.6
x= 0.3m
hL=0.2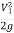 
A1 = 
* d12 = 
* 0.32 = 0.0706m2
A2 = 
*d22 = 
* 0.152 = 0.0176 m2
h = x [1-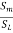 
] = 0.3 [1- 
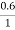] = 0.12m
Applying Bernoulli’s eqn at section 1& 2
:. 
+ 
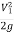+ Z1 =
+
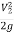+ Z2+ hL
(
- 
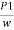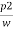) + (Z1-Z2) =
- 
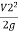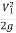+ hL
Applying Continuity eqn at section (1) & (2)
A1V1 =A1 V2
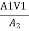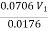= V2
= V2
:. V2 = 4V1
:. (
- 
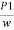) + (Z1-Z2) =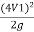
- 
+ 
:. h =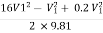 
:. 0.12 =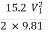 
:.V1 = 0.393m/s
:.Q = A1 V1
= 0.0706 x 0.393
= 0.0277 m3/sec
Reference:
Fluid mechanics – R.K. Rajput
Fluid mechanics & hydraulic machines. – R.K. Bansal
