UNIT 1
Stress and strain
To finalize the material for an engineering product or application is it important to understand the mechanical properties of the material. The mechanical properties of a material are those which affect the mechanical strength and ability of a material to be molded in suitable shape. Some of the typical mechanical properties of a material include:
- Strength
- Toughness
- Hardness
- Hardenability
- Brittleness
- Malleability
- Ductility
- Creep and Slip
- Resilience
- Fatigue
Strength
It is the property of a material which opposes the deformation or breakdown of material in presence of external forces or load. Materials which we finalize for our engineering products must have suitable mechanical strength to be capable to work under different mechanical forces or loads.
Toughness
It is the ability of a material to absorb the energy and gets plastically deformed without fracturing. Its numerical value is determined by the amount of energy per unit volume. Its unit is Joule/ m3. Value of toughness of a material can be determined by stress-strain characteristics of a material. For good toughness, materials should have good strength as well as ductility.
For example: brittle materials, having good strength but limited ductility are not tough enough. Conversely, materials having good ductility but low strength are also not tough enough. Therefore, to be tough, a material should be capable to withstand both high stress and strain.
Hardness
It is the ability of a material to resist to permanent shape change due to external stress. There are various measure of hardness – Scratch Hardness, Indentation Hardness and Rebound Hardness.
- Scratch Hardness
Scratch Hardness is the ability of materials to the oppose the scratches to outer surface layer due to external force. - Indentation Hardness
It is the ability of materials to oppose the dent due to punch of external hard and sharp objects. - Rebound Hardness
Rebound hardness is also called as dynamic hardness. It is determined by the height of “bounce” of a diamond tipped hammer dropped from a fixed height on the material.
Hardenability
It is the ability of a material to attain the hardness by heat treatment processing. It is determined by the depth up to which the material becomes hard. The SI unit of hardenability is meter (similar to length). Hardenability of material is inversely proportional to the weld-ability of material.
Brittleness
Brittleness of a material indicates that how easily it gets fractured when it is subjected to a force or load. When a brittle material is subjected to a stress it observes very less energy and gets fractures without significant strain. Brittleness is converse to ductility of material. Brittleness of material is temperature dependent. Some metals which are ductile at normal temperature become brittle at low temperature.
Malleability
Malleability is a property of solid materials which indicates that how easily a material gets deformed under compressive stress. Malleability is often categorized by the ability of material to be formed in the form of a thin sheet by hammering or rolling. This mechanical property is an aspect of plasticity of material. Malleability of material is temperature dependent. With rise in temperature, the malleability of material increases.
Ductility
Ductility is a property of a solid material which indicates that how easily a material gets deformed under tensile stress. Ductility is often categorized by the ability of material to get stretched into a wire by pulling or drawing. This mechanical property is also an aspect of plasticity of material and is temperature dependent. With rise in temperature, the ductility of material increases.
Creep and Slip
Creep is the property of a material which indicates the tendency of material to move slowly and deform permanently under the influence of external mechanical stress. It results due to long time exposure to large external mechanical stress with in limit of yielding. Creep is more severe in material that are subjected to heat for long time. Slip in material is a plane with high density of atoms.
Resilience
Resilience is the ability of material to absorb the energy when it is deformed elastically by applying stress and release the energy when stress is removed. Proof resilience is defined as the maximum energy that can be absorbed without permanent deformation. The modulus of resilience is defined as the maximum energy that can be absorbed per unit volume without permanent deformation. It can be determined by integrating the stress-strain cure from zero to elastic limit. Its unit is joule/m3.
Fatigue
Fatigue is the weakening of material caused by the repeated loading of the material. When a material is subjected to cyclic loading, and loading greater than certain threshold value but much below the strength of material (ultimate tensile strength limit or yield stress limit), microscopic cracks begin to form at grain boundaries and interfaces. Eventually the crack reaches to a critical size. This crack propagates suddenly and the structure gets fractured. The shape of structure affects the fatigue very much. Square holes and sharp corners lead to elevated stresses where the fatigue crack initiates.
External actions.
Stress:
When a material is subjected to an external force, a resisting force is set up in the component. The internal resistance force per unit area acting on a material is called the stress at a point. It is a tensor quantity having unit of N/m2 or Pascal.
Force (F) is expressed in Newton (N) and A, original area, in square meters (m2), the stress σ will be expresses in N/m2. This unit is called Pascal (Pa).
- As Pascal is a small quantity, in practice, multiples of this unit is used.
Types of Stresses
- Normal stress
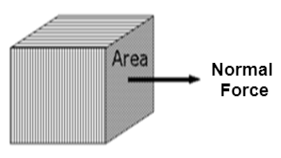
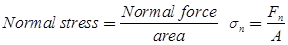
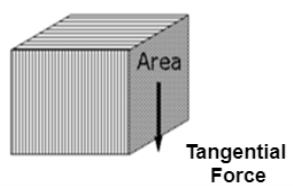
- Shear Stress
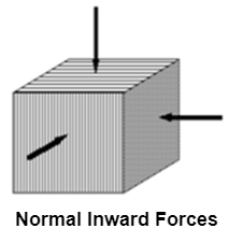
- Bulk Stress
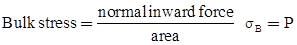
STRAIN
It is the deformation produced in the material due to simple stress. It usually represents the displacement between particles in the body relative to a reference length.
Types of Strains
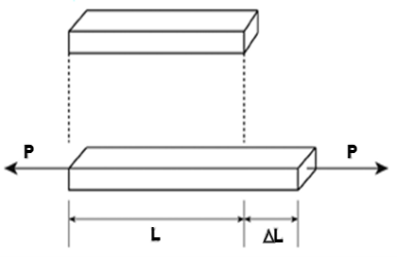
- Normal Strain:
The normal strain of a body is generally expressed as the ratio of total displacement to the original length.
Normal Strain 
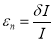
Since strain is m/m, it is dimensionless.
It is of two types: Longitudinal strain and Lateral Strain
- The longitudinal strain is defined as the ratio of the change in length of the body due to the deformation to its original length in the direction of the force.
- Lateral Strain is defined as the ratio of the change in length (breadth of a rectangular bar or diameter of a circular bar) of the body due to the deformation to its original length (breadth of a rectangular bar or diameter of a circular bar) in the direction perpendicular to the force.
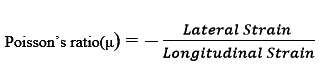
- Shear strain
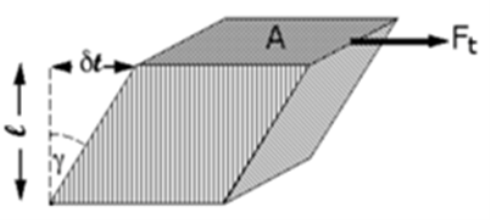
Note 1: The angle is radians, not degrees. The volume of the solid is not changed by shear strain.
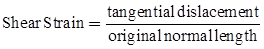
Note: the angle is radians, not degrees
- Bulk Strain or Volumetric Strain
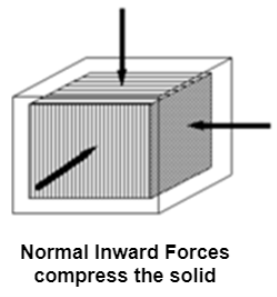
Bulk strain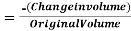
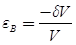
Stress-Strain Relationship
- The stress-strain diagram is shown in the figure. In brittle materials, there is no appreciable change in the rate of strain. There is no yield point and no necking takes place.
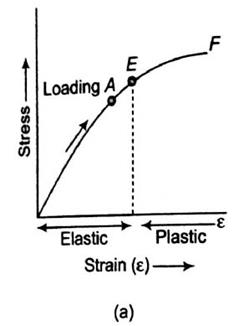
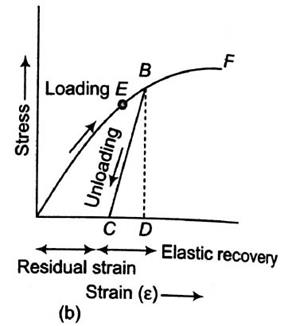
- In figure (a), the specimen is loaded only upto point A, when load has gradually removed the curve follows the same path AO and strain completely disappears. Such behaviour is known as elastic behaviour.
- In figure (b), the specimen is loaded upto point B beyond the elastic limit E. When the specimen has gradually loaded the curve follows path BC, resulting in a residual strain OC or permanent strain.
Comparison of engineering stress and the true stress-strain curves shown below:
- The true stress-strain curve is also known as the flow curve.
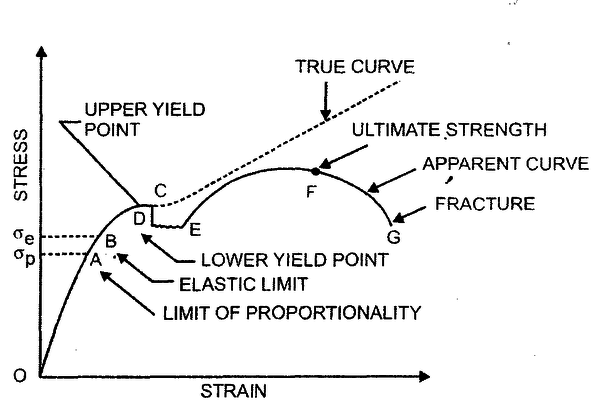
- True stress-strain curve gives a true indication of deformation characteristics because it is based on the instantaneous dimension of the specimen.
- In engineering stress-strain curve, stress drops down after necking since it is based on the original area.
- In true stress-strain curve, the stress, however, increases after necking since the cross-sectional area of the specimen decreases rapidly after necking.
- The flow curve of many metals in the region of uniform plastic deformation can be expressed by the simple power law.
σT = K(εT)n
Where K is the strength coefficient
- n is the strain hardening exponent
- n = 0 perfectly plastic solid
- n = 1 elastic solid For most metals, 0.1< n < 0.5
Hook's Law
According to Hook’s law the stress is directly proportional to strain i.e. normal stress (σ) ∝ normal strain (ε) and shearing stress ( ζ ) ∝ shearing strain ( γ ).
- σ = Eε and ζ = γG
- The co-efficient E is called the modulus of elasticity i.e. its resistance to elastic strain. The coefficient
- G is called the shear modulus of elasticity or modulus of rigidity.
Elastic behavior of the body under external action
- Elasticity is the ability of a body to resist any permanent change to it when stress is applied. When stress application ceases, the body regains its original shape and size. Different materials show different elastic behaviour. The study of the elastic behaviour of a material is of much importance.
- Almost every engineering design requires knowledge of the elastic behavior of materials. In the construction of various structures like bridges, columns, pillars, beams, etc. knowledge of the strength of the materials used in the construction is of prime importance.
Temperature Stress in/members in Parallel [Composite section]
Consider a Composite member formed by joining a steel rod & copper rod as drawn in fig-1.
If both the materials are allowed to expand freely then change in length of copper will be 
and in steel 
.
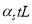Let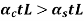 
Refer fig-2
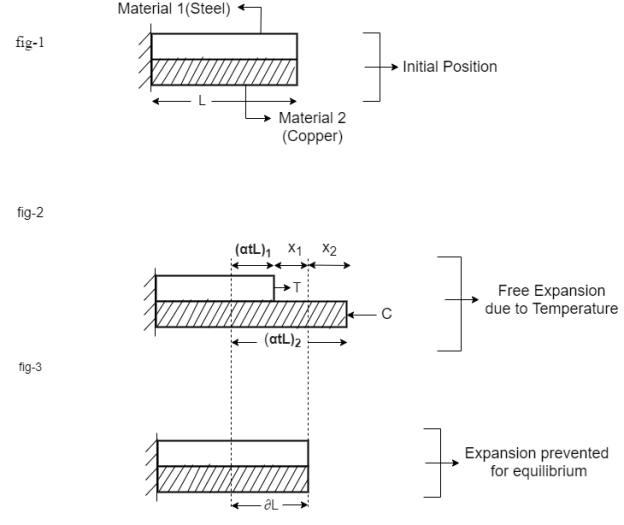
When Equilibrium in reached, the tensile force exerted by copper on steel will be equal to compressive force exerted by steel on copper Refer fig -3.
For a composite section final deformation is same i.e., If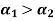 
and temperature rises.
Compression in material 1= Tension in material 2
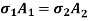
Total Elongation of Steel = Total Elongation of copper
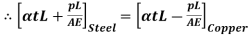
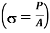
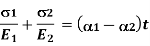
Total Stain 
Deformation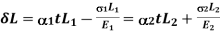 
Composite Member in Series
Consider a member ABC is held in supports at A & C as shown in fig – 1.
When temperature is raised compressive stresses are developed in each portion and when Temperature is lowered tensile stresses are developed in each portion.
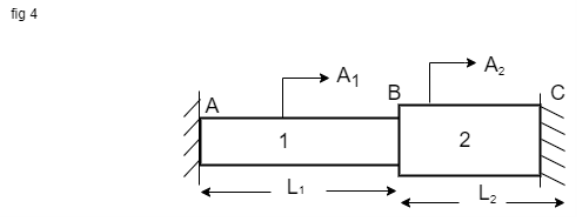
Let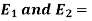 
Young’s Modulus of Portion 1 & 2.
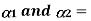Coefficient of linear Expansion in 1 and 2.
Free Expansion due to Temperature Variation.
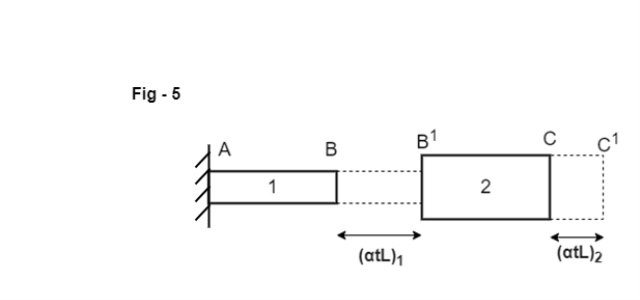
BB’ & CC’ is the free Expansion of Member 1 & 2.
Free Expansion = 
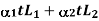….(a)
Let R be the re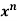
exerted by the supports.
Deformation due to reaction
(R=
)
=
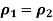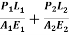….(B)
Equation of Compatibility
Free Expansion – Deformation due to reaction =0
Free expansion = deformation due to Reaction
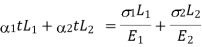
If supports are yields.
Free expansions due to temperature – gap =Deformation due to Reaction
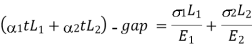
Elastic Constants
Different elastic constants are as follows:
- Young’s modulus
- Bulk modulus
- Rigidity modulus
- Poisson’s ratio
1. Young’s Modulus
According to Hooke’s law, when a body is subjected to tensile stress or compressive stress, the stress applied is directly proportional to the strain within the elastic limits of that body. The ratio of applied stress to the strain is constant and is known as Young’s modulus or modulus of elasticity.
Young’s modulus is denoted by letter “E”. The unit of modulus of elasticity is the same as the unit of stress which is megapascal (Mpa). 1 Mpa is equal to 1 N/mm2.
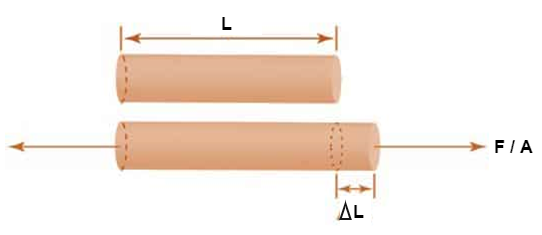
Fig 1: Body Subjected to Tensile Stress
2. Bulk Modulus
When a body is subjected to mutually perpendicular direct stresses which are alike and equal, within its elastic limits, the ratio of direct stress to the corresponding volumetric strain is found to be constant. This ratio is called bulk modulus and is represented by letter “K”. Unit of Bulk modulus is Mpa.
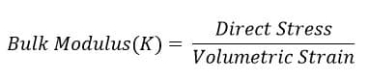
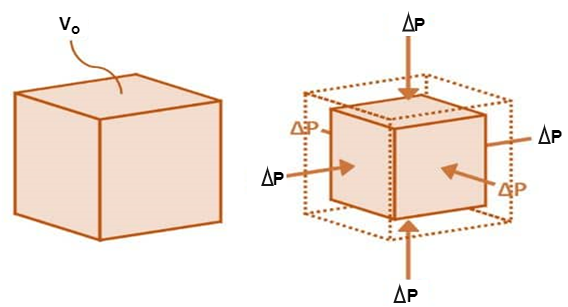
Fig 2: Volumetric Change of Body
3. Rigidity Modulus
When a body is subjected to shear stress the shape of the body gets changed, the ratio of shear stress to the corresponding shear strain is called rigidity modulus or modulus of rigidity. It is denoted by the letters “G” or “C” or “N”. Unit of rigidity modulus is Mpa.
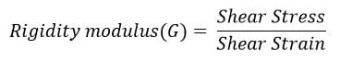
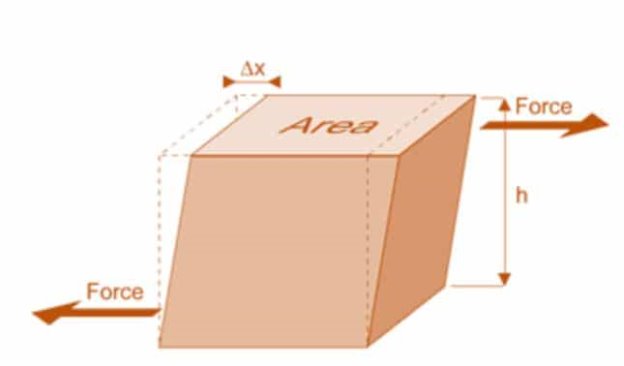
Fig 3: Shear Deformation of Body
4. Poisson’s Ratio
When a body is subjected to simple tensile stress within its elastic limits then there is a change in the dimensions of the body in the direction of the load as well as in the opposite direction. When these changed dimensions are divided with their original dimensions, longitudinal strain and lateral strain are obtained.
The ratio of the lateral strain to the longitudinal strain is called Poisson’s ratio. It is represented by the symbol “µ”. Poisson’s ratio is maximum for an ideal elastic incompressible material and its value is 0.5. For most of theengineering materials, Poisson’s ratio lies between 0.25 and 0.33. It has no units.
Relationship between Elastic Constants
- The relationship between Young’s modulus (E), rigidity modulus (G) and Poisson’s ratio (µ) is expressed as :
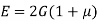
- The relationship between Young’s modulus (E), bulk modulus (K) and Poisson’s ratio (µ) is expressed as :
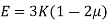
- Young’s modulus can be expressed in terms of bulk modulus (K) and rigidity modulus (G) as :
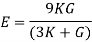
- Poisson’s ratio can be expressed in terms of bulk modulus (K) and rigidity modulus (G) as
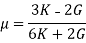
A body is said to be under tri-axial loading when it is subjected to three loads, which are mutually perpendicular in direction say x,y,z directions.
Consider a Rectangular specimen subjected to three tensile stresses, which one mutually perpendicular to each other, as shown in fig.
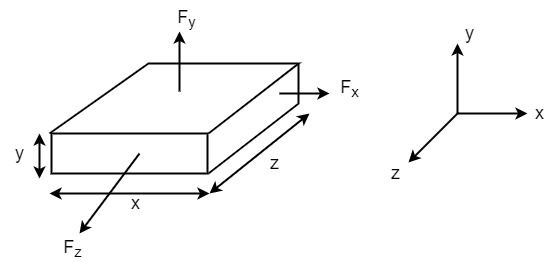
Let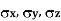 
be stresses in three dimensions (All stresses are Tensile).
, 
, 
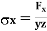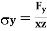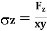
Strain in X – direction
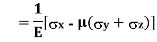
Strain in Y– direction
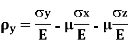
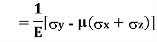
Strain in X – direction
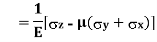
Volume Strain 
=
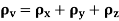
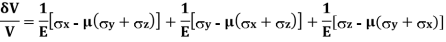
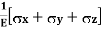[1-2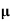
]
