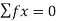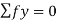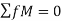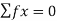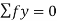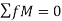UNIT 3
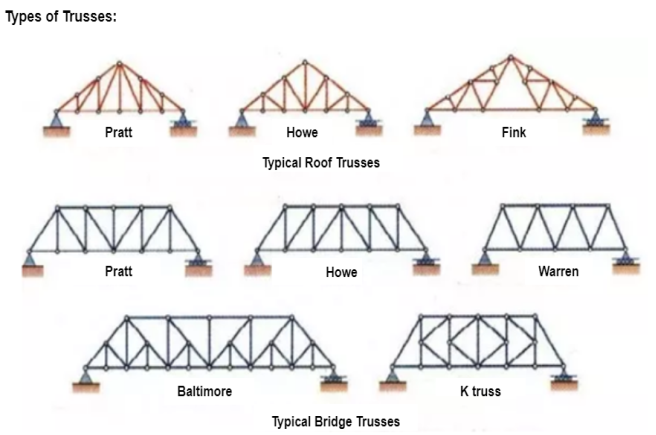
Analysis of trusses
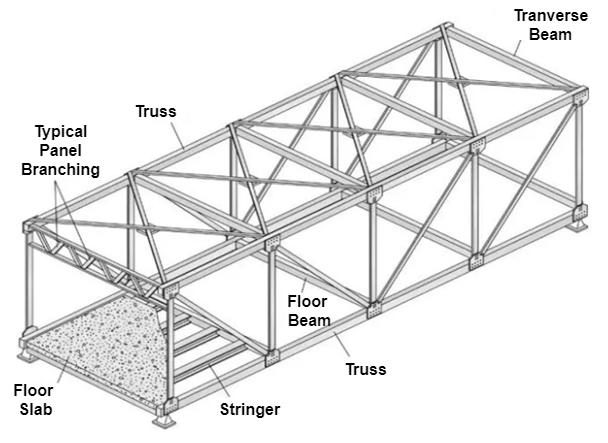
A TRUSS IS A STRUCTURE THAT CONSIST OF
- All Straight members
- Connected together with pin joints
- Connected only at the ends of the members
- All external forces (loads & reactions) must be applied only at the joints.
- Trusses are assumed to be of negligible weight (compared to the loads they carry)
Degree of Static Indeterminacy
- DS = m+re – 2j where, DS = Degree of static indeterminacy m = Number of members, re = Total external reactions, j = Total number of joints
- DS = 0 ⇒ Truss is determinate
If Dse = + 1 & Dsi = –1 then DS = 0 at specified point. - DS > 0 ⇒ Truss is indeterminate or redundant.
Types of Support Reaction in Analysis of Trusses:
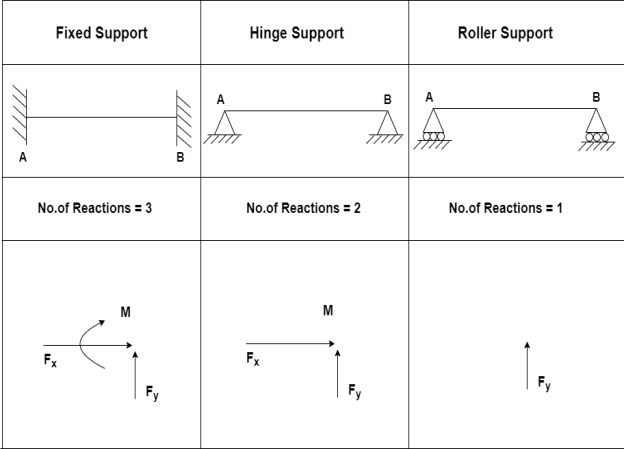
Analysis of Trusses:
Method of Joint:
- Draw FBD
- Check for perfect Truss
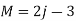Where M = No. Of members
No of joints
- Apply Equilibrium Conditions to whole Truss:
[Moment will be zero, where maximum number of forces passes through that point]
Find all support Reaction forces
- Now Take each joint separately
Apply Equilibrium conditions to Each Joints
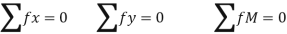
And find the forces in each member
Method of Section:
- Draw FBD
- Check for perfect Truss
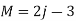where M = No. Of members
No of joints
- Apply Equilibrium Conditions to whole Truss:
[Moment will be zero, where maximum number of forces passes through that point]
Find all support Reaction forces
- Apply rule of Method of Section.
Rule: Cut the section of Truss along the Maximum No. Of member can cut.
Then choose easy truss or simple truss to find out forces in the members by applying equilibrium conditions.
