UNIT 4

Bending stresses

4.1 Theory of pure bending

Pure bending ( Theory of simple bending) is a condition of stress where a bending moment is applied to a beam without the simultaneous presence of axial, shear, or torsional forces.

Pure bending occurs only under a constant bending moment (M) since the shear force (V), which is equal to 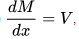  {\displaystyle {\frac {dM}{dx}}=V}, has to be equal to zero.

In reality, a state of pure bending does not practically exist, because such a state needs an absolutely weightless member. The state of pure bending is an approximation made to derive formulas.

Assumptions made in the theory of pure bending

1. The material of the beam is homogeneous1 and isotropic2.
2. The value of Young's Modulus of Elasticity is same in tension and compression.
3. The transverse sections which were plane before bending, remain plane after bending also.
4. The beam is initially straight and all longitudinal filaments bend into circular arcs with a common centre of curvature.
5. The radius of curvature is large as compared to the dimensions of the cross-section.
6. Each layer of the beam is free to expand or contract, independently of the layer, above or below it.

Pure Bending:

A  Simply supported beam ABCD subjected to tow equal point load W at equal – distance ‘a’ from each support a shown in fig.

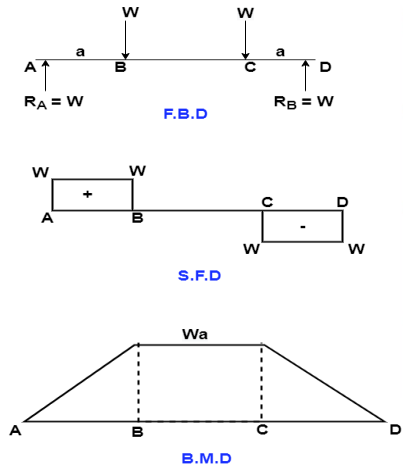
In S.F.D the shear force between portion BC is Zero as shown in fig.

IN B.M.D, the B.M between portions BC is constant.

The portion BC is said to be under pure bending.

4.2 Flexural formula

Derivation of flexure formula for pure bending:

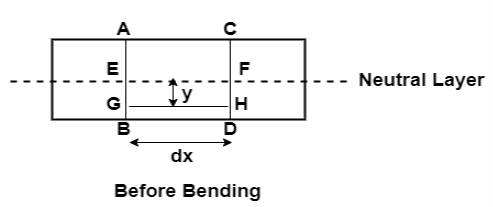
Consider any two normal sections AB and CD of a beam for a small length ‘dx’  apart as shown in fig. After the action of the transverse loading on the beam, the beam will be bends A’ B’ C’ D’ as shown in fig Below.

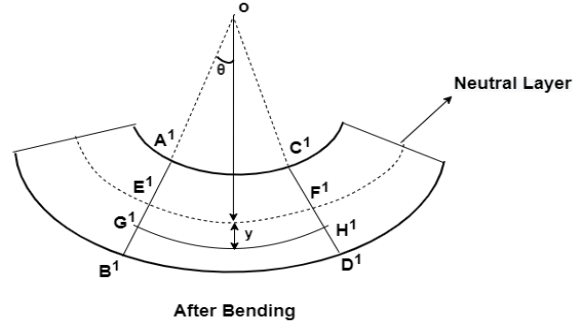
Let A’ B’ and C’ D’ intersect each other at O.

Let R= Radius of curvature of Neutral layer EF.

= Subtended angle at 0.

Consider a layer GH at a distance y from Neutral Axis.

Strain in layer GH due to bending

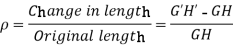
But GH=EF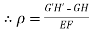   

From fig – 2

Length of arc = Subtended angle × Radius

Original length E’F; = EF = R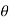

Length of layer G’H’ = (R+y)

Change in length = G’H’-GH=(R+y)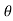 – R

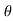
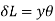
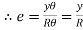   ….(1)

By definition, Modulus of elasticity

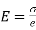
….(2)

From the Equations 1 and 2

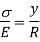
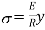      ….. (3)

Since E and R are constant, the stress is directly proportional to the distance from Neutral axis.

Now consider cross-section of the beam.

Consider an elemental strip at ‘y’ from N.A and Area of strip ‘dA’

Force on the strip = stress on the strip × Area on the strip

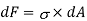
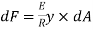
Moment of this force about N.A

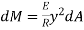
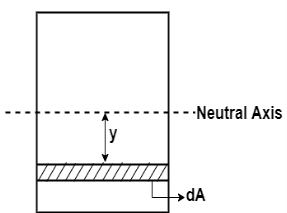
Total Moment of whole section about N.A

M =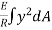

But 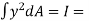Moment of Inertial about Neutral Axis

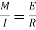   ….(4)

This is known as Bending formula or flexure formula

4.3 Bending stress for symmetrical & unsymmetrical section

• Symmetrical bending:

The plane of loading or the plane of bending is co-incident with or parallel to, a plane containing principal centroidal axes of inertial of the cross-section of the beam.

• Beam stress is given by

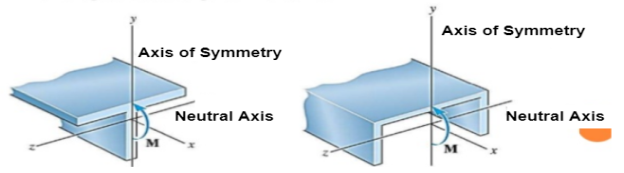
Unsymmetrical Bending

Assumptions

• The plane sections of the beam remain plane after bending
• The material of the beam is homogeneous and linearly elastic.
• There is no net internal axial force.

Sign convention and notation:

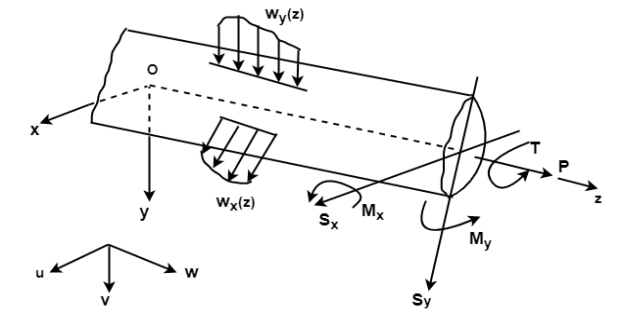
• U,v and w are the displacement components of any point within beam parallel x,y,z axes.
• P=axial load and T=torque
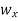• (z) and 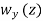are distributed loads
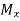• and 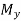are applied bending moments

We assume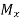 and 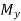as positive when they each induce tensile stresses in the positive xy quadrant of the beam section.

IMPORTANCE OF UNSYMMETRICAL BENDING

• If the plane of bending or plane of loading does not lie in or parallel to theplane that contains the principal centroidal axes of cross-section, thebending is called as unsymmetrical bending.

• Members that are not symmetrical about the vertical axes and which aretypically composed of thin unsymmetrical sections (e.g. ISA, Channel) undergo phenomenon of twisting under the transverse loads.
• A channel section carrying the transverse load would twist because the lineof action of the load does not pass through shear centre of the member.

• Whereas rectangular beam would not twist because the loading would passthrough the centre of gravity of the section and for such two axissymmetrical section the shear centre would coincide with the cg of thesection.

• If one is desired to use unsymmetrical sections to carry transverse loadswithout twisting, it is possible to do so by locating the load so that it passesthrough the shear centre of the beam.