UNIT – 5
Shear stresses in beam
Introduction
In the earlier chapter, the variation of bending stress across a beam section was studied. The bending stress is due to bending moment at the section.
The bending stress act longitudinally and its intensity is directly proportional to its distance from neutral axis.
A typical beam section is subjected to shear force in addition to bending moment. The variation of shearing stress, which is due to the presence of shear force, is studied in this chapter.
The stresses induce by shear force at a section in a beam may be analyzed as follows:
Consider an elemental length of a bem between the sections AA and BB separated by a distance
, as shown in the following figure. Let the moments acting at AA and BB be M and M+dM respectively.
Let CD be a fibre of thickness dy at a distance y from the neutral axis. Then bending stress at left side of the fibre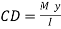 
Force on the left side of the layer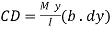 
and force on the right side of the layer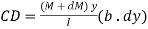 
Therefore unbalanced force, towards right, on the layer CD is =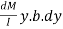
There are a number of such elements above the section .
Hence the unbalanced horizontal force above the section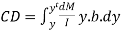 
This horizontal force is resisted by the resisting force provided by shearing stresses acting horizontally on the plane at CD.
Let the intensity of shear stress be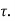 
Equating the resisting force provided by the shearing stress to the unbalanced horizontal force we have
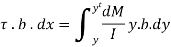
Or,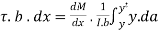 
where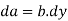 
is area of the element.
Where the term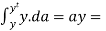
Moment of, area above the fibre CD about the N/A.
But the term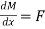 
, the shear force. Substituting in the expression for 
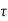, we obtain;
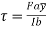where
F = shear force at a section in a beam
a = Area above or below a fibre (shaded area)
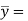Distance from N.A to the centroid of the shaded area
I = M.I of the entire section about the N.A
b = breadth of the fibre.
Note: The above expression is for horizontal shear stress. From the principle of complementary shear, this horizontal shear stress is accompanied by a verical shear stress of the same intensity.
Shear Stress variation of some cross-sections:
(i) Rectangular cross section
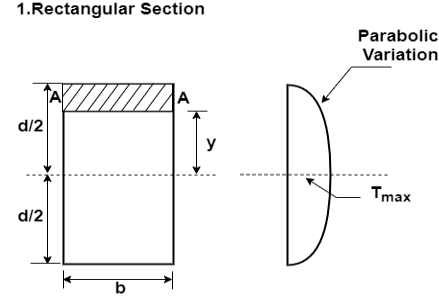
Consider a rectangular of width b and depth d subjected to shearing force F. Let AA be a fibre at a distance y from the neutral axis as shown in fig.
From the equation for shear stress;
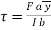where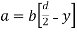 
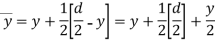
And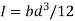 
substituting ,
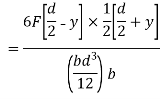
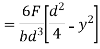
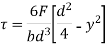
Thus the shear stress variation is parabolic. When,
i) at 
Ii) at 
Iii)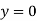 
, 
is maximum and its value is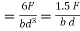 
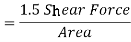
That is,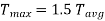 
, for a rectangular section, and this occurs at the neutral axis. Where
Ii) Circular cross section
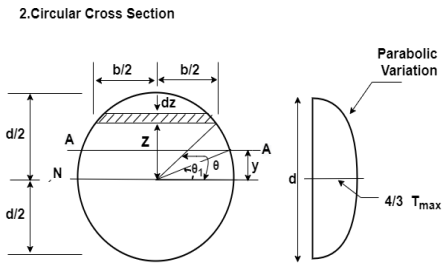
Consider a circular section of diameter d, as shown in fig. Let AA be a fibre at a vertical distance y and angle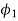 
as shown in fig.
Area of the element, A = b dz
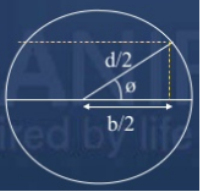
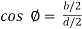
Width of the element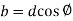 
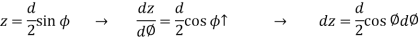
Area of the element,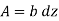 
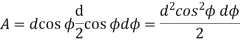
Moment of area of the element about the N.A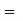 
Area × z
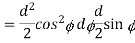
Therefore moment of the entire area, above the fibre AA,
About the N.A =
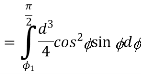
If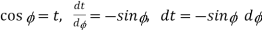 
, and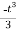 
is integration
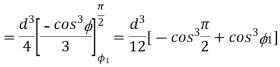
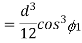
Moment of inertial of the section, 
Substituting in the expression for shear stress,
=
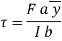
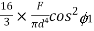
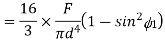
Where b= width of the fibre AA =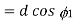 
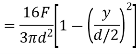
Hence the shear stress varies parabolically over the depth. Its value is zero at the extreme fibres where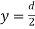 
and its value is maximum when 
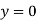at the N.A and is given by
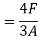
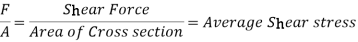
Thus in circular sections shear stress is maximum at the centre and is equal to 4/3 times the average shear stress.
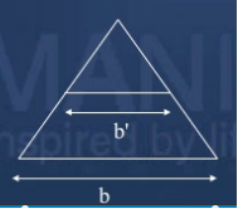
Iii. Isosceles Triangular Section:
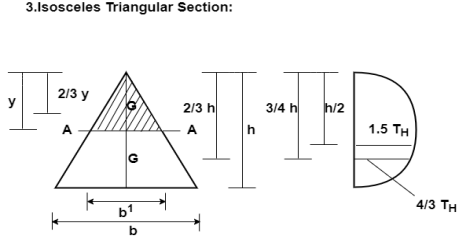
Let AA be a fibre at a distance y rom the top.
Shear stress in general,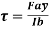 
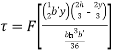….(1)
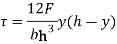
i) at y=0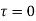 
Ii) at y=h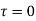 
At the centroid,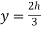 
, substituting in equation 1,
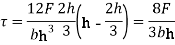
Or,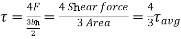 
at the N.A
For shear stress,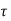 
to be max,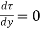 
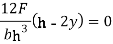
Or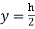 
, substituting in the expression for 
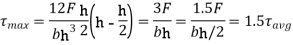
Thus, Maximum shear stress occurs at half the depth and its value is 1.5 times the average shear stress, in the case of an isosceles triangle.
