Unit 5
Theodolite Traversing
- Theodolite traversing is a method of establishing control points, their position being determined by measuring the distances between the traverse stations and the angles subtended at the various stations by their adjacent stations.
- The angles are measured by using theodolite and the distance are measured by using the measurement tape or chain.
Purpose or objectives-
- Theodolite traversing is used to compute the area of a traverse.
- To make a traverse survey.
- To make the field data, adjusting a traverse and plot the results graphically.
- To find the elevation or height of a pole or building indirectly.
- To find the horizontal, vertical and inclined distances indirectly etc.
- Types of Traverse
A Traverse may be of two types.
- Open Traverse
- Closed Traverse
1. Open Traverse
A traverse is said to be open traverse when the traverse starts at one point and terminates at another point as shown in the figure. Open traverse is also called as unclosed traverse. It is suitable for surveying of roads, coastal lines, etc.
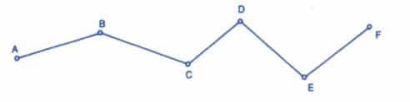
Fig 1: Open Traverse
2. Closed Traverse
A traverse is said to be closed traverse when the traverse formed a closed circuit as shown in the figure. In this case, both starting and terminating points of the traverse coincide with each other. It is suitable for the survey of boundaries of ponds, sports grounds, forests, etc.
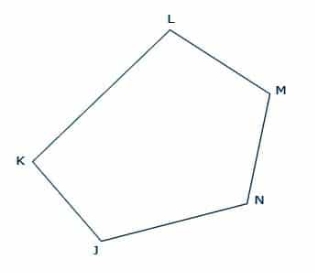
Fig 2: Closed Traverse
Methods of Traversing
The traversing is performed by four different methods and these methods are classified according to the survey instrument used. The methods are as follows.
- Chain Traversing
- Compass Traversing
- Theodolite Traversing
- Plane Table Traversing
1. Chain Traversing
Chain traversing is done by taking linear measurements only. Hence, chain or tape is enough for chain traversing. The angle between the adjacent traverse lines is measured using the chain angles concept. Chain traversing is performed in areas such as ponds etc. where it is difficult to adopt triangulation.
The chain angles concept is nothing but finding the angle between two adjacent sides by establishing the third side using tie stations. This angle between the sides can also be fixed by establishing a chord of known length between the sides.

Fig 3: Survey Chain
2. Compass Traversing
In the case of compass traversing, both linear and angular measurements of traverse lines are taken by using chain and prismatic compass respectively. Both fore bearing and back bearings are measured and required corrections for local attraction are applied. If any closing error is obtained while plotting of traverse, then Bowditch rule is applied for the adjustment of error.

Fig 4: Survey Compass
3. Theodolite Traversing
In the case of theodolite traversing, the linear measurements are done by using chain or stadia method and angular measurements are done by theodolite. Using theodolite, the magnetic bearing of the first traverse line is measured and from that magnetic bearing of other sides are calculated. This method is very accurate compared to other methods.

Fig 5: Theodolite Traversing
4. Plane Table Traversing
In the case of plane table traversing, the measuring and plotting of the traverse on the paper are done simultaneously. The plane table equipment is set up at every traverse station one by one in a clockwise or anti-clockwise direction. The sides of each traverse station are drawn on paper to a suitable scale. If there is any closing error, graphical methods are used for its adjustment.

Fig 6: Plane Table Traversing
Sometimes it becomes very difficult to measure all bearing and measurements due to field condition like a river or some other obstacles and for this some reading may be omitted.
Cases for omitted measurement
There is some common types of omitted measurement in closed traverse that is as follow.
- Length of one line is omitted.
- Length of two lines are not measured.
- Length of one line and bearing of other line are not measured.
- Bearing of one line is missing.
- Bearing and length of same line are missing.
- Bearing of two lines are missing.
This cases is usually seen when there is some obstacles like river is between taking reading in field in theodolite surveying.
Length of one line is omitted/ Bearing of one line or both is missing.
When we calculated traverse and there is bearing or length of one line is missing then it is known by using the method that is as follow.
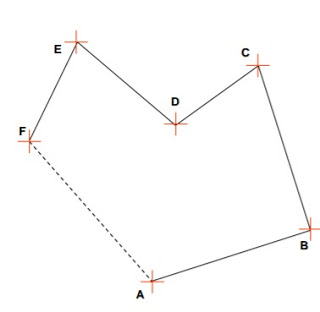
- First a traverse is ABCDEF that is closed traverse.
- There is length of the line FA is missing or bearing of line FA is missing or both bearing and length is not measured.
- We can calculate the ΣL' and ΣD' for the five sides that we know.
- Therefore we can calculate ΣL' and ΣD' for AB, BC, CD, DE and EF.
If the length of unknown side is l and angle is x and the latitude is L and departure is D then we can find L and D as follow.
ΣL = 0
ΣL = L+ ΣL'
So,
L+ ΣL' = 0
ΣL' = -L
OR
L = -ΣL'
By same calculation we get departure of unknown
D = -ΣD'
From the above equations, we can know departure and latitude of unknown side.
If we want to find length or bearing of that side than we can calculate it as follow.
Bearing of unknown x is
x = arctan(ΣD'/ΣL')
and length of that side is
l = √(ΣL'²+ΣD'²)
So, we can find latitude, departure, bearing and total length of the one line that is omitted.
This is case when one line's information is omitted but as we see previously that there may be other case such as length of two sides omitted. For that we have to use different method to finding that length.
Let's see method for two sides of traverse.
Length of two lines are omitted.
This become difficult because we cannot directly use latitude or departure to calculate. There is different method that give us a way to know in this condition.
- First consider the traverse ABCDEF.
- This traverse is closed traverse, for this there is two sides are unknown that is EF and FA.
- Other sides of length is measured that is AB, BC, CD, DE.
- For this we can assume that ABCDE is closed traverse with the all information is known.
- For that traverse, length of EA is calculated by method of case of when one length omitted.
- Now we can assume the triangle for which is is easy to calculate the length of sides.
- Therefore, consider triangle AEF.
- In this triangle, one length is known and the all angles of triangle can be calculated.
Assume that this angle is x, y and z then we can calculate unknown length from the basic equations of triangle.
EF/sinx = FA/siny= EA/sinz
From this we have the all angles and one length EA, so we can for length EF,
EF = EA sinx/sinz
and the other unknown length
FA = EA siny/sinz
Therefore we can find both unknown length and after finding this we can calculate departure and latitude of it.
Reference Books:
1. Principles of Surveying. Vol. I by J. G. Olliver, J. Clendinning - Van Nostrand
Reinhold.
2. Plane Surveying by A. M. Chandra, New Age International Publishers.
3. Surveying Vol. I & II by Dr. K. R. Arora, Standard Book House.
4. Plane surveying – David Clark.