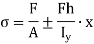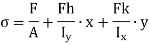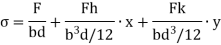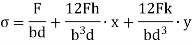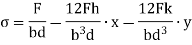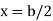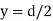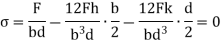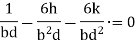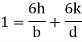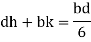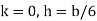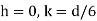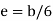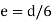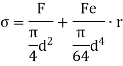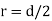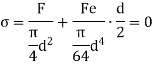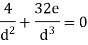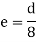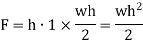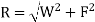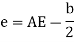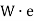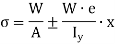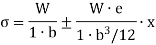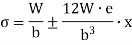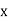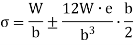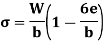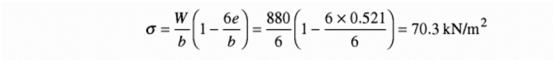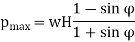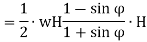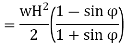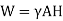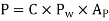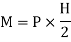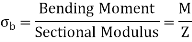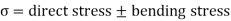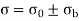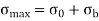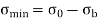Unit-2

Combined Direct and Bending Stresses

2.1 Combined Direct and Bending Stresses, eccentric load, core/kernel of section

Combined Direct and Bending stresses for eccentric loading

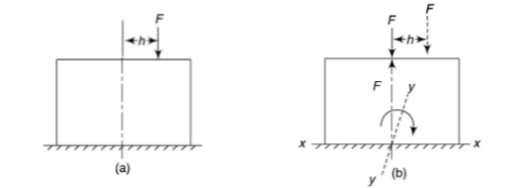
Let a column be acted upon by a thrust F, the line of action of which cuts the cross-section at a point on the x-axis at a distance h from the centroid O. If two equal and opposite forces are introduced along the axis of the column, then the system becomes equivalent to the load at O that produces a uniform direct stress along with a bending moment 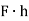about y-axis, producing a varying bending stress.

Fig. 1 Eccentric loading on column

Then the combined compressive stresses at any point at a distance 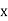from YY,

Where, A is the cross-sectional area

If 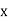taken positive on the same side of the y-axis as the load, then bending stress will be of same type of direct stress and taken and positive. On left side, 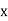is negative and thus the sign taken is negative. And thus at the left edge o the section, stress will depend upon the value of the right term of the above equation i.e. it is more or less.

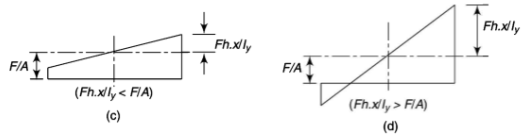
Stress distribution is given below:

Fig. 2 Stress distribution

The above condition is when the load is eccentric to one axis.

In case, when load is eccentric to both axes as shown below.

Fig. 3 Load eccentric to both axis

It will be equivalent to central load and bending moment about the two axes.

In the above equation, x and y are taken positive when on the same side of the axes as of the load.

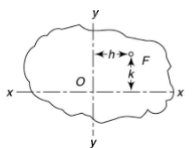
Core/kernel of a section

In masonry column, it is desirable that tensile stresses are not set up. It is achieved if the line of action of load lies within the central area of the section. This central area is called as kernel or core of the section.

Shape of the kernel depends on the profile of the section.

Middle Third rule for rectangular section

Consider the rectangular section with width b and depth d.

Fig. 4 Core for rectangular section

This equation gives the limiting values of h and k. In each quadrant the load must lie in the line produced by this equation.

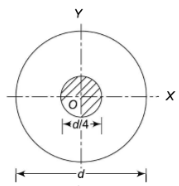
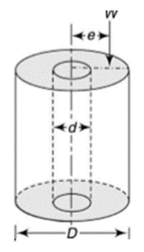
Middle Quarter rule for circular section

Consider the circular section with diameter d as shown below

Fig. 5 Core for circular section

The equation gives the limiting value of eccentricity for all possible positions of the load. The kernel is the circle of diameter 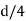with center O. To avoid tensile stress, load must lie within this section.

1. Example 1: A short column of rectangular section 160 mm x 120 mm carries a load of 200 kN. The load point is at a point 40 mm from the longer side and 70 mm from the shorter side. Determine the maximum tensile and compressive stresses in the section

2.     Example 2: A short column of external and internal diameters as D and d respectively carries an eccentric load W.  Determine the maximum eccentricity which the load can have without producing the tension on the cross-section of the column.

2.2 Stability Analysis of gravity dam, retaining wall and chimney

Stability of gravity dam:

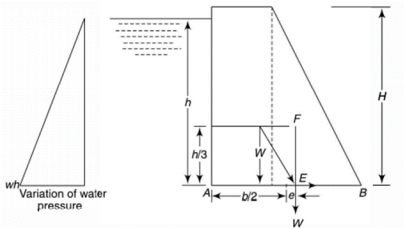
A dam is a structure to store water and to provide head to a power house. Consider as dam as shown in figure.

Let H and h be the height of dam and of water on the upstream side respectively.

There are two main forces acting on the dam:

• Force of static water pressure
• Weight of dam

Consider a unit length of dam.

Let W be the weight of the dam acting downward through center of gravity of weight of dam.

If w is the specific weight of water, then wh is the water pressure at the bottom of the dam and its variation is linear, zero at the surface of water and maximum (wh) at the bottom of dam.

Total water force acting on the dam,

As the water pressure varies linearly from top to bottom, the center of force is at H/3 from the bottom of the dam.

If b is the width of the dam at the bottom,

Resultant thrust is given by,

Let it intersect the bottom of the dam at E.

Horizontal component of R at E is equal to F. This is resisted by the frictional force at the base against sliding.

Vertical component of R at E is equal  to W and is balanced by the resultant of stress forces at the bottom.

The vertical component W at E induces

• Normal compressive stress at the base due to load W and
• Normal compressive and tensile stresses due to bending moment induced due to eccentricity of load

Eccentricity of loading,

Then the combined stress at any point at a distance 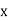from midpoint of the base,

This indicates that point E must lie between b/6 from midpoint of the base, otherwise the term in the bracket will become negative and tensile stress will occur at the base.

Example: A gravity dam is 10 m high. Its width at the top and bottom is 2 m and 6 m respectively. Its water face is vertical and retains water to a depth of 9 m. Determine the maximum and minimum stress values at the base. The weight of the dam is 22 kN/m3 and specific weight of water 9.81 kN/m3.

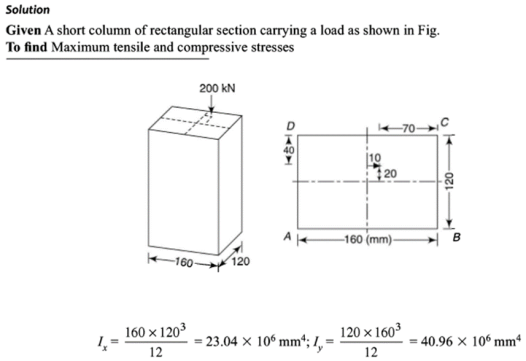
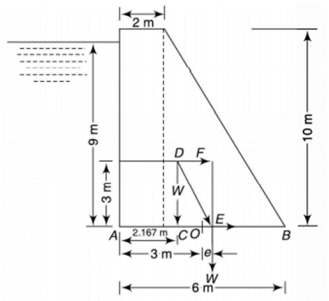
Solution:

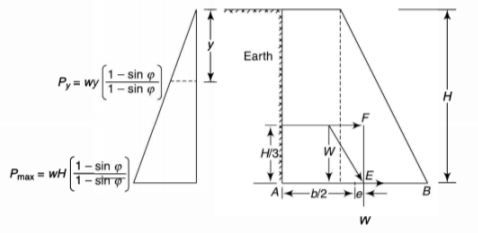
Stability of retaining wall:

Materials having loose particles such as sand, clay earth, gravel, ash and mud take the shape of a cone when placed freely on a surface. The angle of the cone varies from material. This means that if such a material is placed near a wall, the volume of material which is prevented on the wall varies zero at the top of each to a maximum at the bottom.

The material retained by the wall is known as backfill which may have its top surface horizontal or inclined. The backfill above the horizontal plane at the top of a wall is known as surcharge. In the design of retaining walls, it is necessary to determine the lateral pressure exerted by the retaining mass of soil.

Angle of Repose: It is the natural slope of the materials when placed on a horizontal surface in the absence of any external acting force. For most of the materials, its value varies between 20o and 40o.

Rankine’s Formula: This formula provides the earth pressure at any depth y from the top of the retaining wall. It is given by

Where 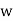is the specific weight of earth and 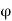is the angle of repose. If H is the height of the wall, then maximum pressure at the bottom is

Total horizontal force = Average pressure x height

This force acts at H/3 from the bottom.

Example: A 12 m high masonry retaining wall of trapezoidal section has a width of 2 m at the top and 8 m at the bottom. The retaining surface is vertical and the wall retains earth which is level up to the top. Determine the maximum and minimum stresses at the base. The densities of the earth and the masonry are 14 kN/m3 and 25 kN/m3 respectively and the angle of repose of the earth is 30o.

Solution:

Stability of Chimney:

Consider a chimney having cross-sectional area A and height H subjected to uniform wind pressure .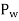

Weight of chimney,

Direct stress at base

Let wind pressure acts on the surface area comes in contact produced bending of structure.

References

1. Strength of Material by S. S. Ratan