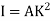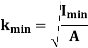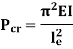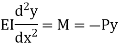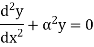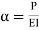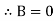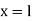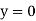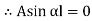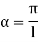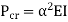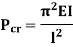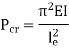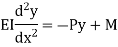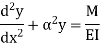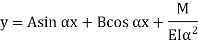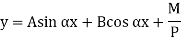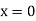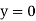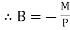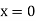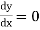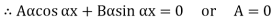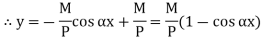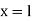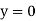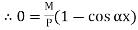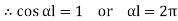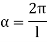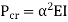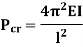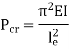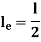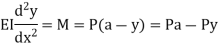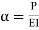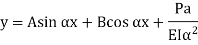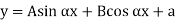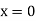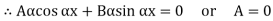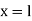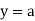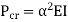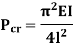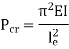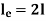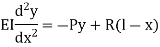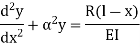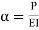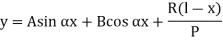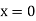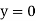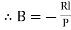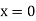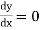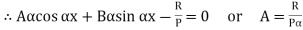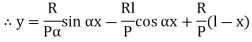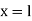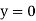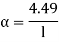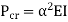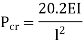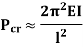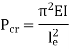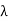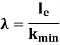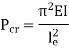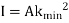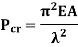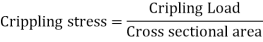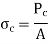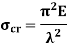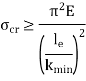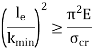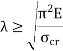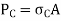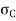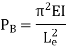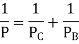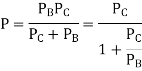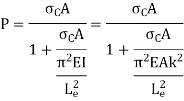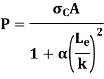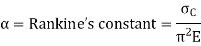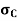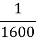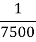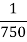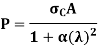Unit-4
Buckling of Long Columns
A member of a structure which carries a axial compressive load is called as strut. If the strut is vertical then it is called as column.
A long, slender column becomes unstable when its axial compressive load reaches a value known as the critical buckling load. If a beam element is set under a compressive load and magnitude of its length is larger than either of its other dimensions such a beam is called a column. Because of its size, its axial displacement is very less than its lateral deflection known as buckling. Buckling doesn’t vary linearly with load but it occurs abruptly and is hence is very dangerous.
Critical Load (crippling load) Pcr
Critical load is the only load for which the structure will be in equilibrium in the disturbed position. If the load on the strut or column exceeds this value, then the column will fail by buckling. At this value the structure is in equilibrium regardless of the magnitude of the angle. At this value, restoring effect of the moment in the spring matches the buckling effect of the axial load represents the boundary between the stable and unstable conditions.
If the axial load is less than Pcr the effect of the moment in the spring dominates and the structure returns to the vertical position after a small disturbance – stable condition.
If the axial load is larger than Pcr the effect of the axial force predominates and the structure buckles – unstable condition.
Because of the large deflection caused by buckling, the least moment of inertia I can be expressed as,
|
Where, A is cross-sectional area of column or strut.
K is the radius of gyration and is given by
|
Note: The smallest radius of gyration of the column, i.e. the least moment of inertia I should be taken in order to find the critical stress.
A swiss mathematician Euler in 1757 derived a formula for stability of long column.
In Euler’s theory, the column fails due to bucking only, effect due to compression is neglected. Also, the effect of direct stress is neglected because direct stress induced in a long column is negligible as compared to bending stress.
This theory is not used for short column because direct stress are considerable and hence cannot be neglected in short column.
According to Euler’s Theory,
Euler’s critical load is given by,
Where, E is Young’s Modulus And I is the least Moment of Inertia
|
Assumptions made in Euler’s Theory
- The column should be axially loaded
- The column material is perfectly elastic, homogeneous and isotropic and hence obeys Hooke’s law.
- The column should be perfectly straight and uniform in cross-section throughout its length
- Length of column is very large as compared its cross-sectional dimensions.
- Direct stress is negligible compared to bending stress.
- Plane cross-section remains plane and normal to the center line during the buckling.
- Self-weight of the column is neglected.
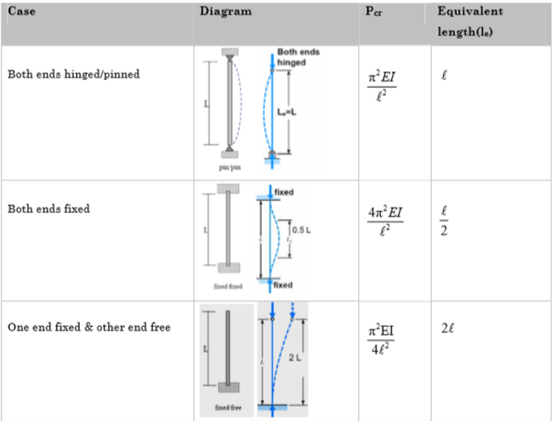
Effective length of column for various end conditions
In Euler’s theory, following cases may be considered.
- Both end’s hinged
|
Fig. 1 Both edges hinged
Y-axis is taken in such a way that deflection is positive.
From the equation of bending, viewing from right end,
The equation can be written as
Where, The solution of the above equation is
When both ends are hinged. At And at If A = 0, y is zero for all values of load, hence, there is no bending.
Therefore, Euler’s Crippling load,
Comparing above equation with
We get,
|
2. Both ends fixed
|
Fig. 2 Both ends fixed
Let M be the end fixing moments, then governing equation becomes,
|
The equation can be written as
|
Where,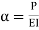 
The solution of the above equation is
|
When one end is fixed and other is free.
At At
|
At
Therefore, Euler’s Crippling load,
Comparing above equation with
We get,
|
3. One end fixed and other free
|
Fig. 3 One end fixed and other free
Take Y-axis towards right for positive value of y. Viewing from left we get,
The equation can be written as Where, The solution of the above equation is
When one end is fixed and other is free. At At
At
Therefore, Euler’s Crippling load,
Comparing above equation with
We get,
|
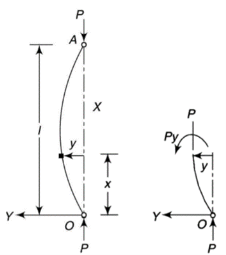
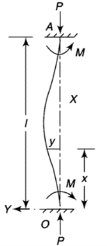
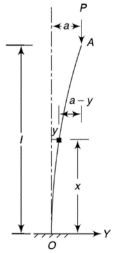
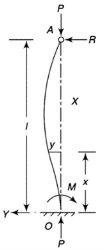
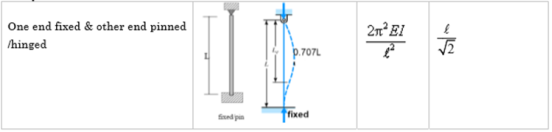
4. One end fixed and other hinged
|
Fig.4 One end fixed and other free
Let M be the fixing moment at end O.
For equilibrium of strut, a horizontal for R acts at free end
Then,
The equation can be written as
Where,
|
The solution of the above equation is
When one end is fixed and other is free. At At
At
Therefore, Euler’s Crippling load,
Comparing above equation with
We get,
|
We can summarize the above conditions as given below:
|
|
Slenderness Ratio
It is the ratio of the length of a column to the least radius of gyration of a column.
It is denoted by
We have,
And
Therefore,
Crippling Stress
|
Limitation of Euler’s Theory
Crippling stress is given by,
|
The critical stress is directly proportional to modulus of elasticity and inversely proportional to square of slenderness ratio of column.
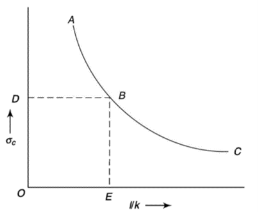
The graph plotted between critical stress and slenderness ratio is shown in figure below.
|
Fig.5 Critical stress v/s slenderness ratio
The value of 
at point B is called as critical value of slenderness ratio.
For any slenderness ratio above this value, column fails for buckling and for any value of slenderness ratio less than this value, the column fails by crushing and not by buckling.
Hence, for short column, Euler’s Formula is not applicable.
Mathematically, Euler’s Formula is applicable,
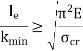
If crushing stress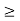 
buckling stress
|
When the slenderness ratio is greater than or equal to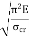 
, then the Euler’s formula is applicable. This is the limitation of Euler’s formula.
Euler’s Theory cannot be applied to short columns. Rankine derived an empirical formula which is applicable for both short and long column.
Short column fails by crushing load.
Where, Long Column fails by buckling load
In general, the column or struts fails due to combined effect of crushing stress and bending stress.
|
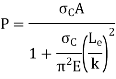
Hence, by Rankine’s formula,
Where
|
Rankine’s constant is a property of the material of the column. Value of Rankine’s constant ‘a’ and crushing value 
for some materials are given below:
Sr. No | Material | Crushing Stress | Rankine’s Constant |
1 | Wrought iron | 250 MPa |
|
2 | Cast iron | 550 MPa |
|
3 | Mild steel | 320 MPa |
|
4 | Timber | 50 MPa |
|
Rankine’s formula can also be written as
|
References
- Strength of Material by S. S. Ratan
