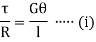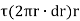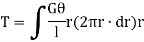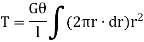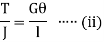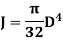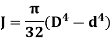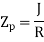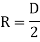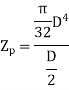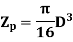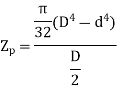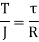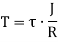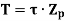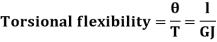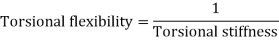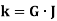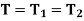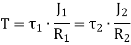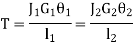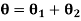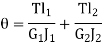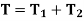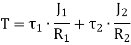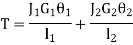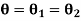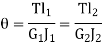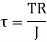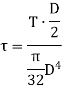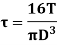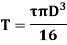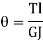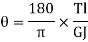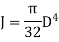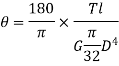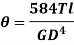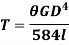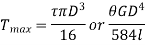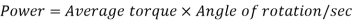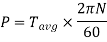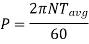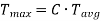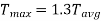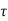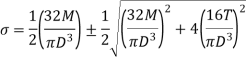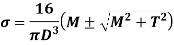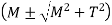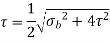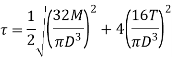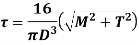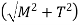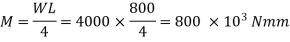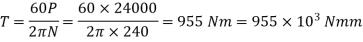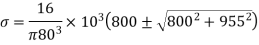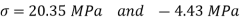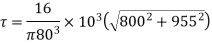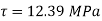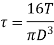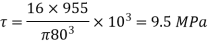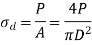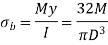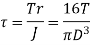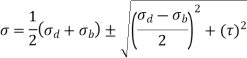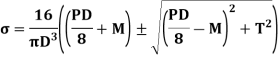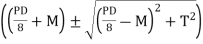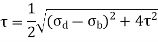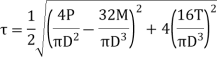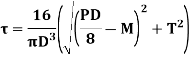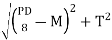Unit-6
Torsion of Circular Shaft
“A member which is subjected to the couple which produce rotation about longitudinal axis is known as Twisting Moment or Torsion.”
- Due to torque applied on shaft, the shaft produced shear stress and shear strain in the materials.
- In practice, torque is produced in shaft of motors or power equipment. e.g. Fans, axles of vehicles, pumps, etc.
When a force is applied tangentially to a cylindrical rod, at a certain radius, in the plane of its transverse cross-section, the rod is said to be subjected to twisting moment or torque. Torsion is also defined as the product of tangential force and the radius.
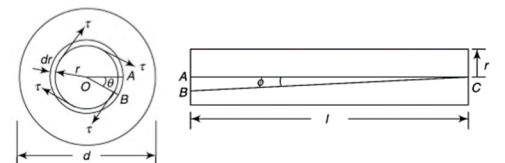
Figure below shows a circular shaft of length l and diameter d acted upon by a torque T.
|
Fig.1 Circular shaft subjected to torque
The shear strain 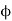 of elements at radial distance r form the axis is constant for a particular value of T. The line OA thus twists to OB.
of elements at radial distance r form the axis is constant for a particular value of T. The line OA thus twists to OB.
Let 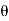 be the angle of twist of a cross-section relative to another cross-section at a distance l apart. Then,
be the angle of twist of a cross-section relative to another cross-section at a distance l apart. Then,
Now, tangential force on the element = Moment of tangential force on the element = Sum of moments for the whole shaft,
|
But 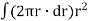 is the polar moment of inertia of the shaft,
is the polar moment of inertia of the shaft,
Thus
From (i) and (ii)
This equation is called as Torsion Equation. |
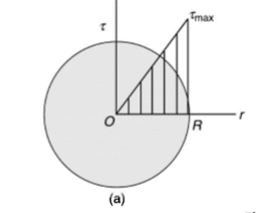
Torsion equation shows that for a given shaft, shear stress is proportional to the radius of shaft. Figure below shows a shear stress distribution in solid shaft of Radius R.
Fig.2 Shear stress distribution
Assumptions in Torsion Theory
- The bar is acted upon by a pure torque.
- The section under consideration is remote from the point of application of the load and from a change in diameter.
- Adjacent cross sections originally plane and parallel remain plane and parallel after twisting, and any radial line remains straight.
- The material obeys Hooke’s law
- Cross-sections rotate as if rigid, i.e. every diameter rotates through the same angle
Basic Torsion Formulae:
Polar moment of Inertia for solid circular shaft with diameter D is given as
Polar moment of Inertia for hollow circular shaft with outer diameter D and inner diameter d is given as
|
B. Polar Sectional Modulus Polar sectional modulus is the ratio of sectional modulus to the maximum radius of shaft. Mathematically,
For solid shaft,
For hollow shaft,
Now, we have from torsion equation,
|
The ability of shaft to resist the motion of twisting moment is called as strength of a shaft.
C. Torsional Stiffness It is the torque required to produce unit angle of twist It is given by,
|
D. Torsional Flexibility It is the angle of twist produced by a unit torque applied
|
E. Torsional Rigidity Torsional rigidity is the product of modulus of rigidity G and polar moment of inertia J It is given by,
|
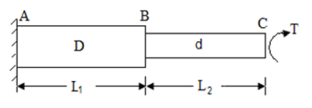
Torsion in stepped and composite shaft:
Stepped or composite shaft are either in series or parallel
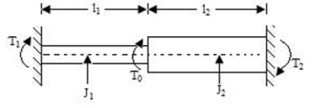
Shafts in series: When the two shafts are joined in series and a single torque is applied, both shafts are subjected to same torque.
Fig. Shaft in series
Also
The angle of twist for the shafts in series is the sum of the angle of twist of each shaft
|
Shaft in Parallel:
Fig.3 Shaft in parallel
When the two shafts are joined in parallel, the torque applied to the composite shaft is the sum of the torques on the two shafts
The angle of twist in the shafts in parallel is same
|
Torque on strength basis
When the shaft is subjected to pure torsional moment, the torsional shear stress is given,
Therefore,
Torque on rigidity basis From Torsion equation, we have,
Value of
For solid shaft, we have
Therefore,
|
Where, 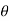 is in degree.
is in degree.
Torque found by strength basis and by rigidity basis is maximum torque.
Therefore,
|
Power transmission by shaft
It is the product of average torque and corresponding angle turned per unit duration of time.
Where, N is in rpm
The relation between average torque and maximum torque is
Where C is a constant, Generally,
|
The condition of combined bending, torsion and axial thrust is frequently encountered. Consider a shaft subjected to combined bending and twisting moment.
In such cases, stresses are set up due to bending moment, torque and shear force. However, shear stress due to shear force is usually unimportant as its maximum value occurs at the neutral axis where the bending stress is zero.
Let,
The for solid shaft under combined couples,
Where, M is the bending couple or bending moment T is the twisting couple or torque D is the diameter of shaft
|
For vertical loading on shaft, the maximum values of bending stress occurs at the ends of vertical diameter whereas maximum value of shear stress at outer surface. As there is no normal stress on the longitudinal planes of the shaft,
Maximum principal stresses are,
Maximum shear stress is,
|
Solution:
Given: L = 800 mm D = 80 mm W = 4 kN P = 24 kW N = 240 rpm
|
Sol:
At the end of vertical diameter, Principle stress is
Maximum shear stress is given by,
At the ends of horizontal diameter, The bending stress is zero Ans hence, maximum shear stress is
|
Combined bending, twisting and axial thrust
Now, consider a shaft subjected to combined bending, twisting and direct axial thrust.
Let P be the axial thrust acting on shaft with diameter D and area of cross section A.
Then direct stress is given by,
Let M be the bending moment y- be the distance of fiber from neutral axis I be the moment of Inertia Then Bending stress is given by,
Let T be the twisting moment or torque acting on the shaft with J as the polar moment of inertia of circular shaft with diameter D=2r Then Shear stress is given by,
Now, when the circular shaft is subjected to combined axial, bending and twisting thrust. |
The resultant maximum principal stresses are given by
Maximum shear stress is,
|
References
- Strength of Material by S. S. Ratan