UNIT 5

 Data-Level Parallelism in Vector, SIMD and GPU Architectures

5.1 Introduction, Vector Architecture, SIMD Instruction Set Extensions for Multimedia, Graphics Processing Units Detecting and Enhancing Loop-Level Parallelism

Flynn’s Taxonomy

Single instruction stream, single data stream (SISD)

Single instruction stream, multiple data streams (SIMD)

Vector architectures

Multimedia extensions

Graphics processor units

Multiple instruction streams, single data stream (MISD)

No commercial implementation

Multiple instruction streams, multiple data streams (MIMD)

Tightly-coupled MIMD

Loosely-coupled MIMD

Introduction

SIMD architectures can exploit significant data-level parallelism for:

Matrix-oriented scientific computing

Media-oriented image and sound processors

SIMD is more energy efficient than MIMD

Only needs to fetch one instruction per data operation

Makes SIMD attractive for personal mobile devices

SIMD allows programmer to continue to think sequentially

SIMD Parallelism

Vector architectures

SIMD extensions

Graphics Processor Units (GPUs)

For x86 processors:

Expect two additional cores per chip per year

SIMD width to double every four years

Potential speedup from SIMD to be twice that from MIMD!

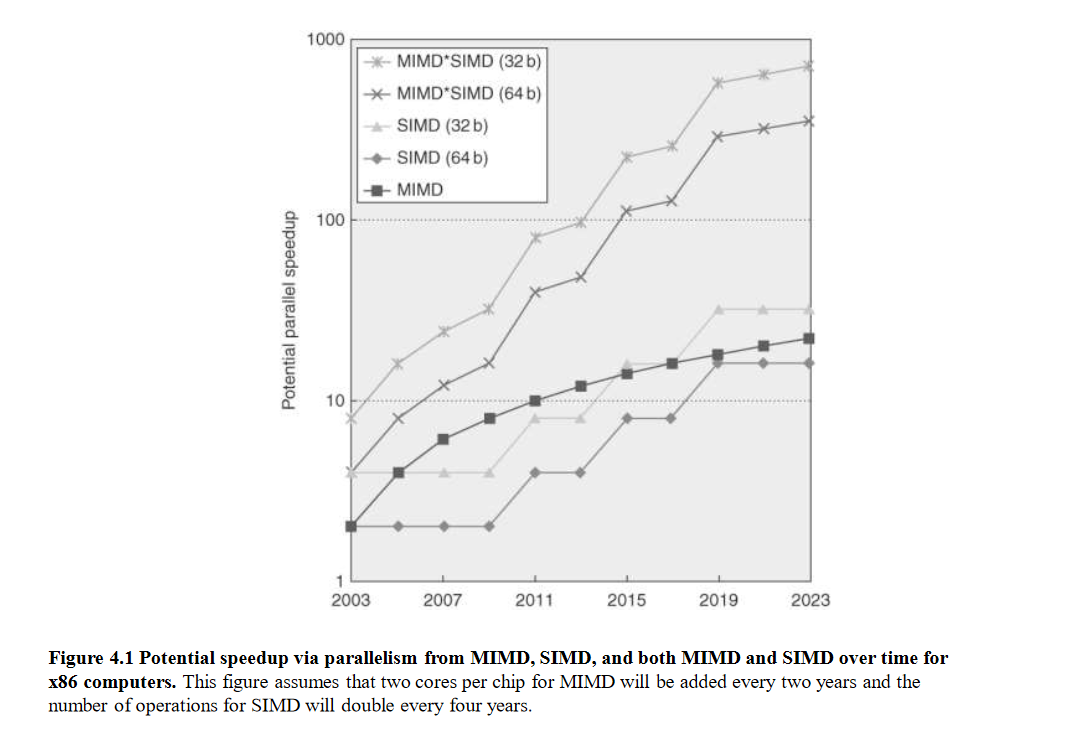
Fig 1 – Potential speedup via parallelism from MIMD,SIMD and both MIMD and SIMD over time for x86 computers

Vector Architectures

Basic idea:

Read sets of data elements into “vector registers”

Operate on those registers

Disperse the results back into memory

Registers are controlled by compiler

Used to hide memory latency

Leverage memory bandwidth

VMIPS

Example architecture: VMIPS

Loosely based on Cray-1

Vector registers

Each register holds a 64-element, 64 bits/element vector

Register file has 16 read ports and 8 write ports

Vector functional units

Fully pipelined

Data and control hazards are detected

Vector load-store unit

Fully pipelined

One word per clock cycle after initial latency

Scalar registers

32 general-purpose registers

32 floating-point registers

Fig 2 – The basic structure of a vector architecture VMIPS

VMIPS Instructions

ADDVV.D: add two vectors

ADDVS.D: add vector to a scalar

LV/SV: vector load and vector store from address

MULVV.D: multiply two vectors

MULVS.D: multiply a vector with a scalar

SUBVV.D: subtract vector from a vector

SUBVS.D: subtract scalar from a vector

SUBSV.D: subtract vector from a scalar

Vector Execution Time

Execution time depends on three factors:

Length of operand vectors

Structural hazards

Data dependencies

VMIPS functional units consume one element per clock cycle

Execution time is approximately the vector length

Convoy

Set of vector instructions that could potentially execute together

Chimes

Sequences with read-after-write dependency hazards can be in the same convey via chaining

Chaining allows a vector operation to start as soon as the individual elements of its vector source operand become available

Chime

Unit of time to execute one convey

M conveys executes in m chimes

For vector length of n, requires mx n clock cycles

Challenges

Start-up timeLatency of vector functional unit

Optimizations:

Multiple Lanes: > 1 element per clock cycle

Vector Length Registers: Non-64 wide vectors

Vector Mask Registers: IF statements in vector code

Memory Banks: Memory system optimizations to support vector processors

Stride: Multiple dimensional matrices

Scatter-Gather: Sparse matrices

Programming Vector Architectures: Program structures affecting performance

Multiple Lanes

Element n of vector register A is “hardwired” to element n of vector register B

Allows for multiple hardware lanes

Fig 3 – Vector load store unit

Vector Length Registers

Vector length not known at compile time?

Use Vector Length Register (VLR)

Use strip mining or vectors over the maximum length

For shorter vectors, we can use a vector length register applied to each vector operation

For longer vectors, we can split the long vector into multiple vectors (of equal, or of maximum plus smaller lengths). The process is called strip-mining.

The strip-mined loop consists of a sequence of convoys.

Memory Banks

Memory system must be designed to support high bandwidth for vector loads and stores

Spread accesses across multiple banks

Control bank addresses independently

Load or store non sequential words

Support multiple vector processors sharing the same memory

Example:

32 processors, each generating 4 loads and 2 stores/cycle

Processor cycle time is 2.167 ns, SRAM cycle time is 15 ns

How many memory banks needed?

32x6=192 accesses,

15/2.167≈7 processor cycles

1344!

Stride

Stride is the distance separating elements in memory that will be adjacent in a vector register. The unit stride is easiest to handle.

Must vectorise multiplication of rows of B with columns of D

Use non-unit stride

Bank conflict (stall) occurs when the same bank is hit faster than bank busy time:

Example:

8 memory banks with a bank busy time of 6 cycles and a total memory latency of 12 cycles. How long will it take to complete a 64-element vector load with a stride of 1? With a stride of 32?

Answer:

Stride of 1: number of banks is greater than the bank busy time, so it takes

12+64 = 76 clock cycles

1.2 cycles per elementStride of 32: the worst case scenario happens when the stride value is a multiple of the number of banks, which this is! Every access to memory will collide with the previous one! Thus, the total time will be:

12 + 1 + 6 * 63 = 391 clock cycles, or 6.1 clock cycles per element!

Scatter-Gather

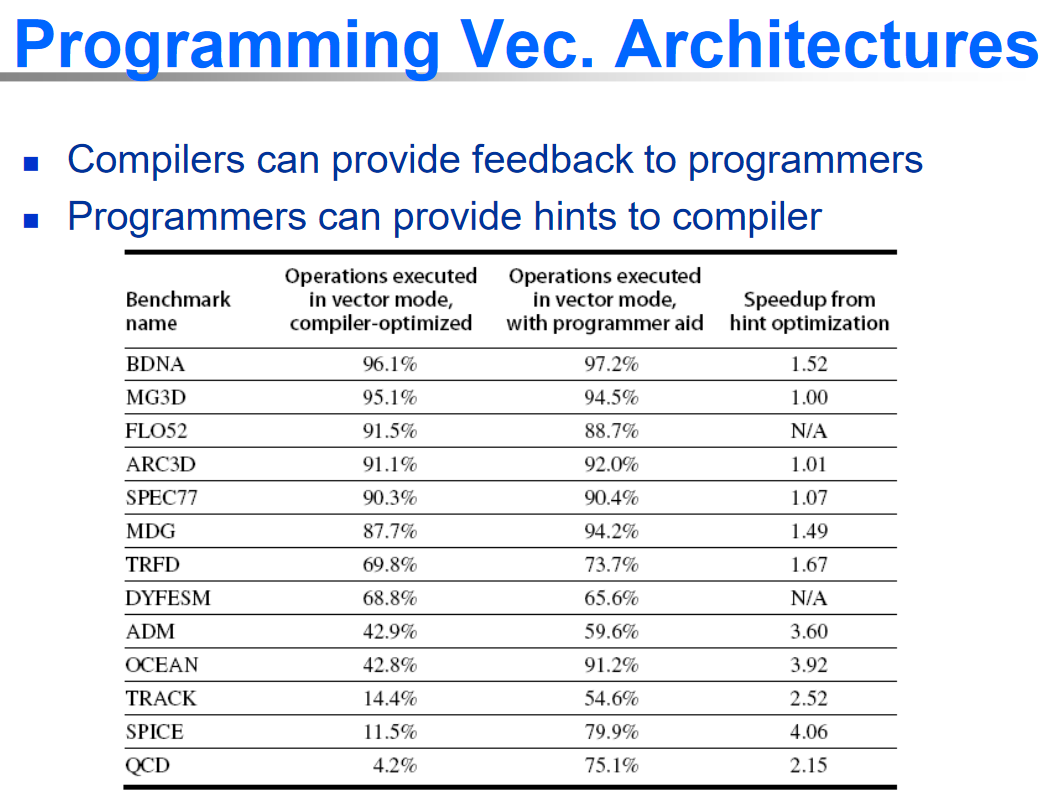
SIMD Extensions

Media applications operate on data types narrower than the native word size

Example: disconnect carry chains to “partition” adder

Limitations, compared to vector instructions:

Number of data operands encoded into op code

No sophisticated addressing modes (strided, scatter-gather)

No mask registers

SIMD Implementations

Implementations:

Intel MMX (1996)

Eight 8-bit integer ops or four 16-bit integer ops

Streaming SIMD Extensions (SSE) (1999)

Eight 16-bit integer ops

Four 32-bit integer/fpops or two 64-bit integer/fpops

Advanced Vector Extensions (2010)

Four 64-bit integer/fpops

Operands must be consecutive and aligned memory locations

Generally designed to accelerate carefully written libraries rather than for compilers

Advantages over vector architecture:

Cost little to add to the standard ALU and easy to implement

Require little extra state

Easy for context-switch

Require little extra memory bandwidth

No virtual memory problem of cross-page access and page-fault

Example SIMD Code

Roofline Performance Model

Basic idea:

Plot peak floating-point throughput as a function of arithmetic intensity

Ties together floating-point performance and memory performance for a target machine

Arithmetic intensity

Floating-point operations per byte read

Fig 4 – Arithmetic intensity

Examples

Attainable GFLOPs/sec Min = (Peak Memory BW ×Arithmetic Intensity, Peak Floating Point Perf.)

Fig 5 - Example

Graphical Processing Units

Given the hardware invested to do graphics well, how can it be supplemented to improve performance of a wider range of applications?

Basic idea:

Heterogeneous execution model

CPU is the host, GPU is the device

Develop a C-like programming language for GPU

Compute Unified Device Architecture (CUDA)

Open CL for vendor-independent language

Unify all forms of GPU parallelism as CUDA thread

Programming model is “Single Instruction Multiple Thread” (SIMT)

Threads and Blocks

A thread is associated with each data element

CUDA threads, with thousands of which being utilized to various styles of parallelism: multithreading, SIMD, MIMD, ILP

Threads are organized into blocks

Thread Blocks: groups of up to 512 elements

Multithreaded SIMD Processor: hardware that executes a whole thread block (32 elements executed per thread at a time)

Blocks are organized into a grid

Blocks are executed independently and in any order

Different blocks cannot communicate directly but can coordinate using atomic memory operations in Global Memory

GPU hardware handles thread management, not applications or OS

A multiprocessor composed of multithreaded SIMD processors

A Thread Block Scheduler

Grid, Threads, and Blocks

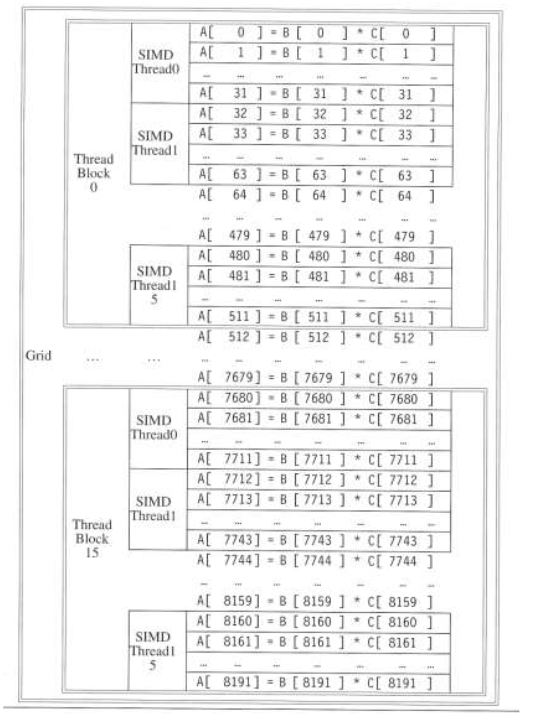
Fig 6 – thread block

NVIDIA GPU Architecture

Similarities to vector machines:

Works well with data-level parallel problems

Scatter-gather transfersMask registers

Large register files

Differences:

No scalar processor

Uses multithreading to hide memory latency

Have many functional units, as opposed to a few deeply pipelined units like a vector processor

Example

Multiply two vectors of length 8192

Code that works over all elements is the grid

Thread blocks break this down into manageable sizes

512 elements/block, 16 SIMD threads/block

32 ele/thread

SIMD instruction executes 32 elements at a time

Thus grid size = 16 blocks

Block is analogous to a strip-mined vector loop with vector length of 32

Block is assigned to a multithreaded SIMD processor by the thread block scheduler

Current-generation GPUs (Fermi) have 7-15 multithreaded SIMD processors

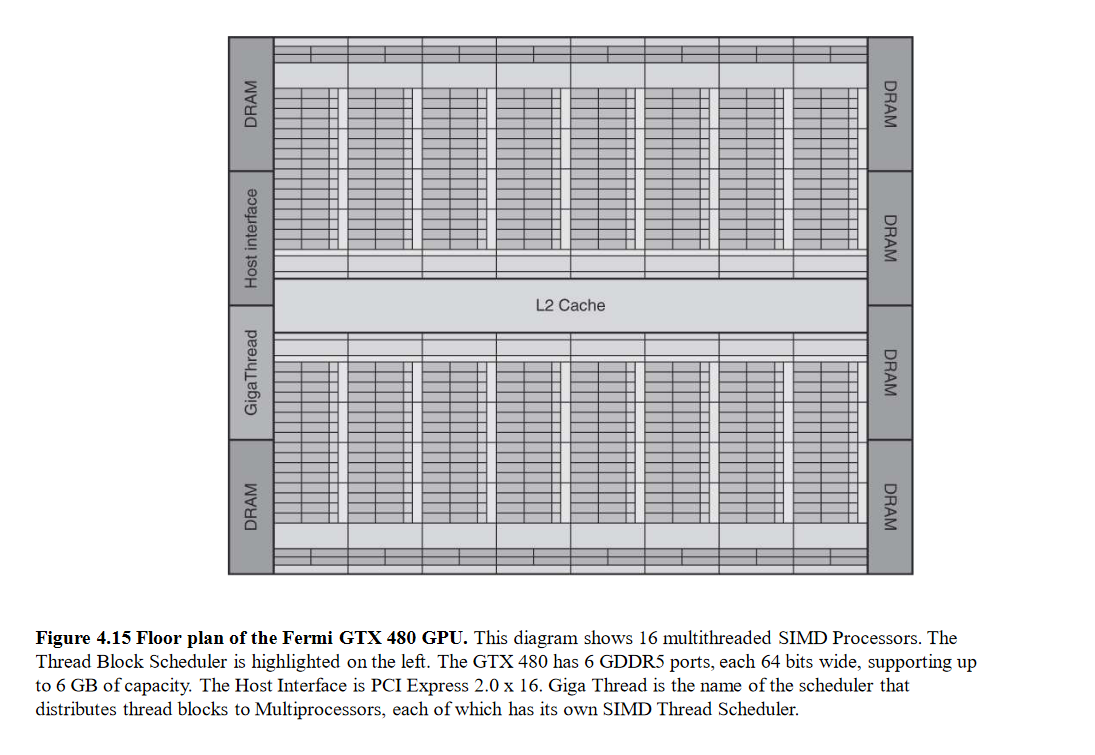
Fig 7 – Floor plan of the Fermi GTX 480 GPU

Terminology

Threads of SIMD instructions

Each has its own PC

Thread scheduler uses scoreboard to dispatch

No data dependencies between threads!

Keeps track of up to 48 threads of SIMD instructions

Hides memory latency

Thread block scheduler schedules blocks to SIMD processors

Within each SIMD processor:

32 SIMD lanes

Wide and shallow compared to vector processors

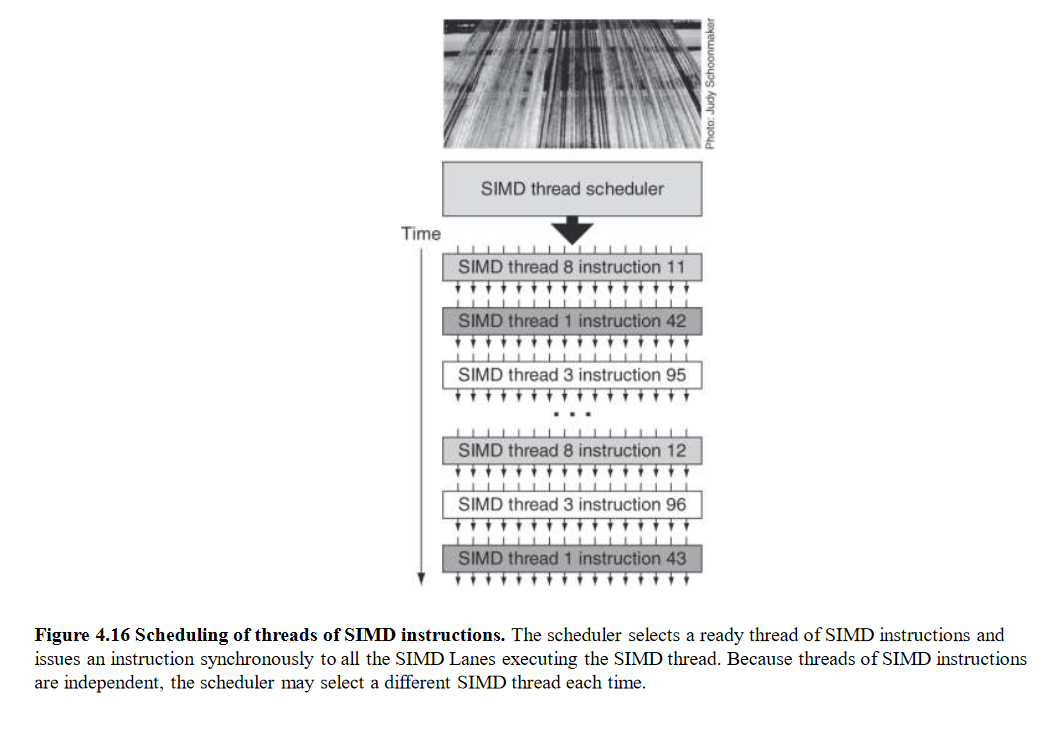
Fig 8 – Scheduling of threads of SIMD instructions

Example

NVIDIA GPU has 32,768 registers

Divided into lanes

Each SIMD thread is limited to 64 registersSIMD thread has up to:

64 vector registers of 32 32-bit elements

32 vector registers of 32 64-bit elements

Fermi has 16 physical SIMD lanes, each containing 2048 registers

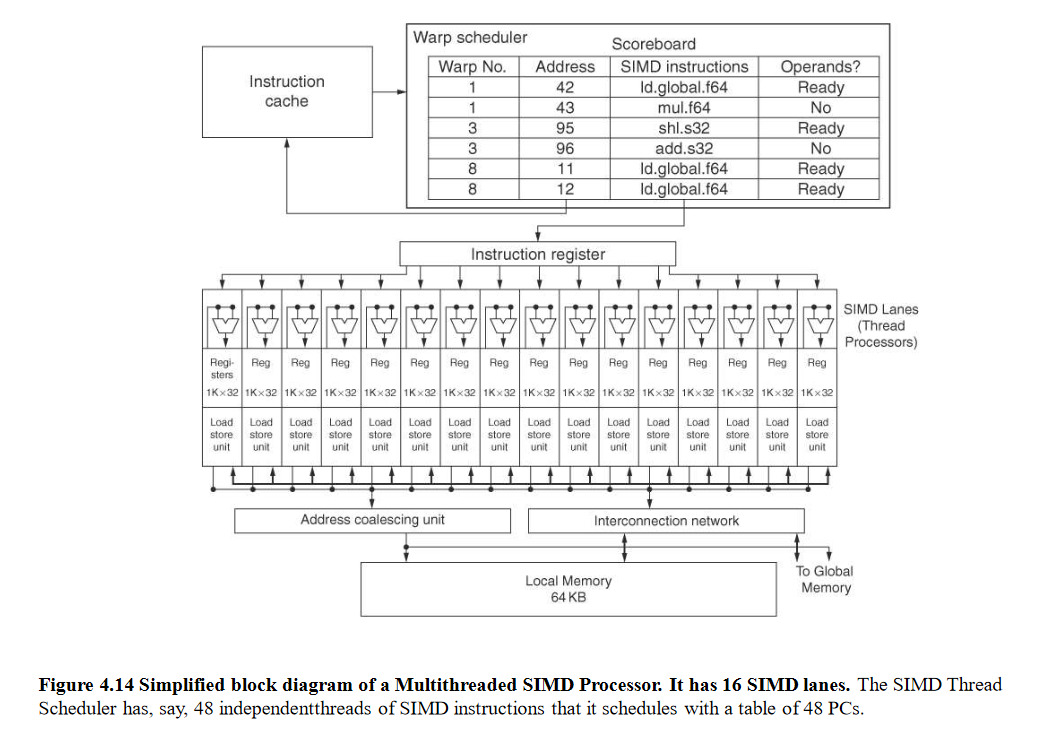
NVIDIA Instruction Set Arch.

Conditional Branching

Like vector architectures, GPU branch hardware uses internal masks

Also usesBranch synchronization stackEntries consist of masks for each SIMD lane

I.e. which threads commit their results (all threads execute)

Instruction markers to manage when a branch diverges into multiple execution paths

Push on divergent branch

...and when paths converge

Act as barriers

Pops stack

Per-thread-lane 1-bit predicate register, specified by programmer

Example

NVIDIA GPU Memory Structures

Each SIMD Lane has private section of off-chip DRAM

“Private memory”, not shared by any other lanes

Contains stack frame, spilling registers, and private variables

Recent GPUs cache this in L1 and L2 caches

Each multithreaded SIMD processor also has local memory that is on-chip

Shared by SIMD lanes / threads within a block only

The off-chip memory shared by SIMD processors is GPU Memory

Host can read and write GPU memory

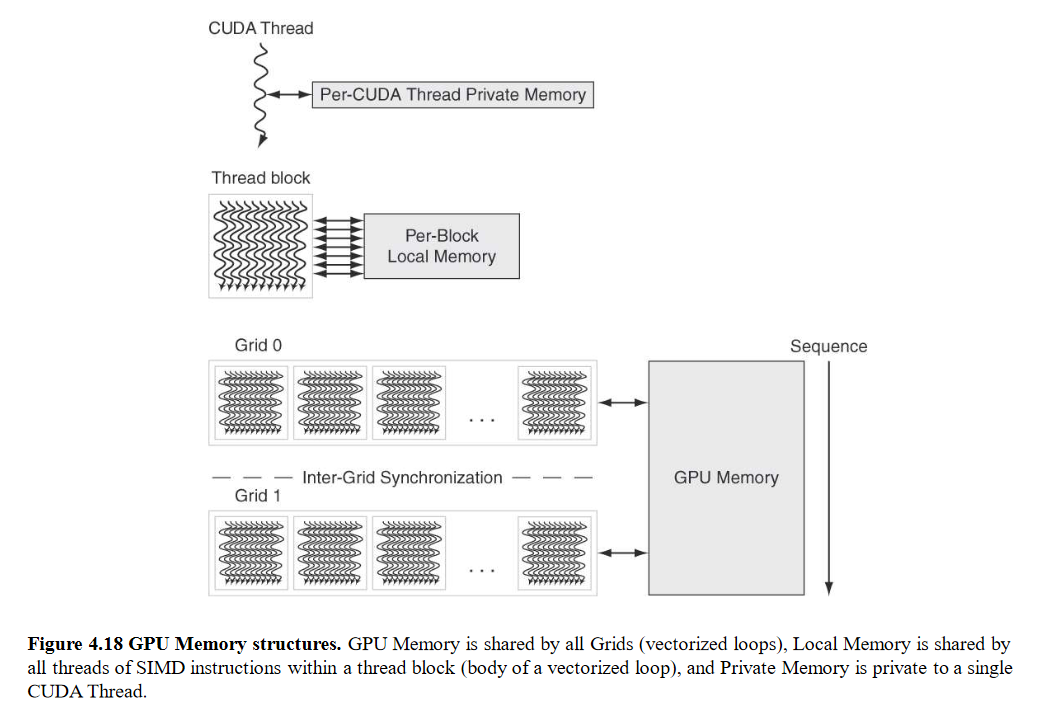
Fig 9 – GPU memory structures

Fermi Architecture Innovations

Each SIMD processor has

Two SIMD thread schedulers, two instruction dispatch units

16 SIMD lanes (SIMD width=32, chime=2 cycles), 16 load-store units, 4 special function units

Thus, two threads of SIMD instructions are scheduled every two clock cycles

Fast double precision: gen-78 515 GFLOPs for DAXPY

Caches for GPU memory: I/D L1/SIMD procand shared L2

64-bit addressing and unified address space: C/C++ ptrs

Error correcting codes: dependability for long-running apps

Faster context switching: hardware support, 10X faster

Faster atomic instructions: 5-20X faster than gen-

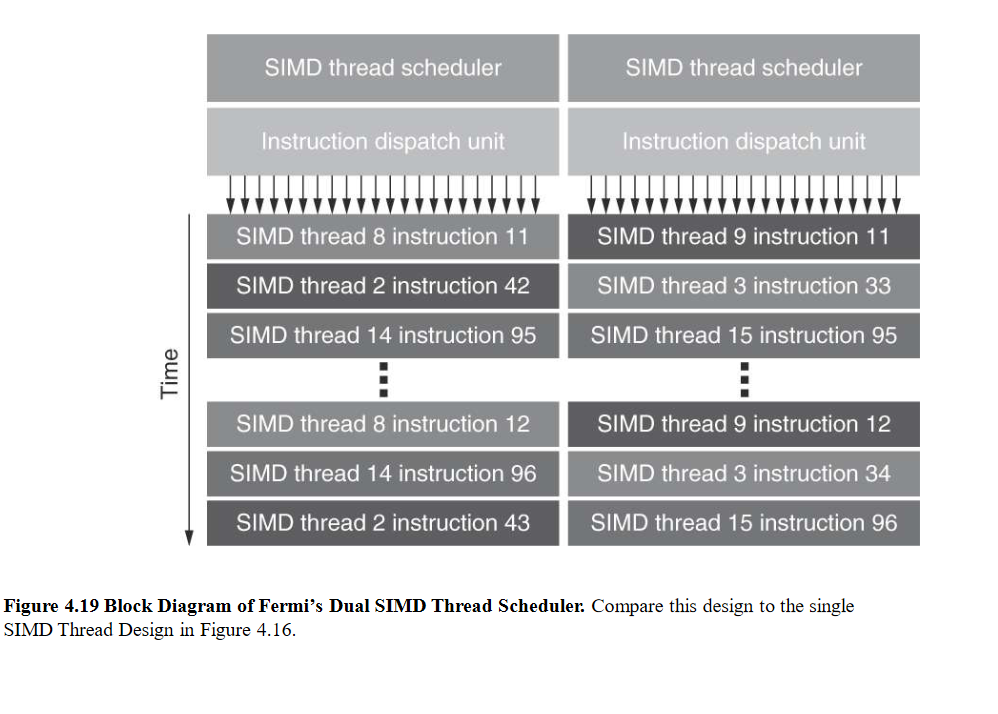
Fig 10 – Fermi dual SIMD thread scheduler

Fermi Multithreaded SIMD Proc.X

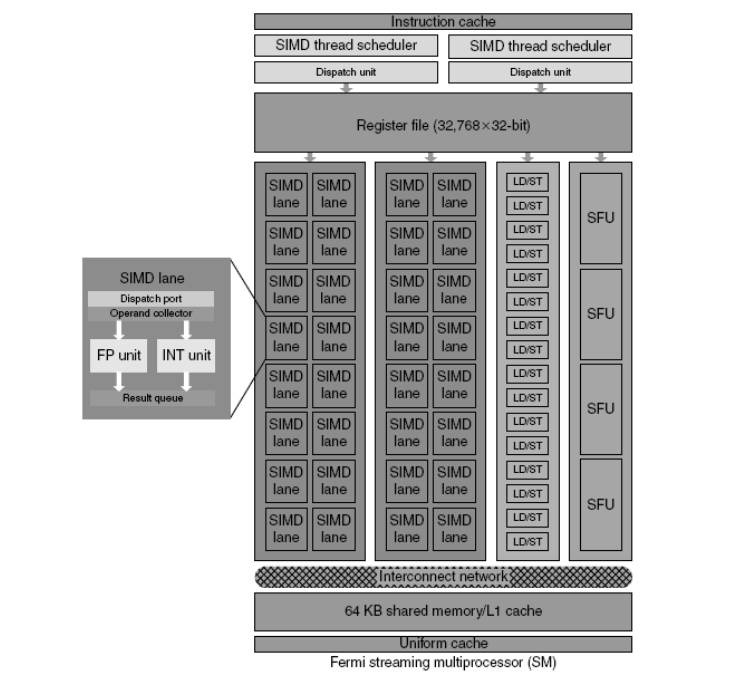
Fig 11 – Fermi streaming multiprocessor

Loop-Level Parallelism

Focuses on determining whether data accesses in later iterations are dependent on data values produced in earlier iterations

Loop-carried dependence

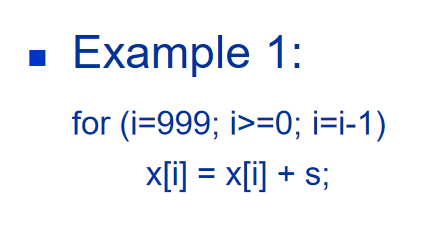
No loop-carried dependence

Finding dependencies

Assume that a 1-Darray index is affine:

ax i+ b (with constants and b)

An index in an n-Darray index is affine if it is affine in each dimension

Assume:

Store to ax i+ b, thenLoad from cx i+ d

I runs from m to n

Dependence exists if:

Given j, k such that m≤ j≤ n, m≤ k≤ nStore to ax j+ b, load from ax k+ d, and ax j+ b= cx k+ d

Generally cannot determine at compile time

Test for absence of a dependence:

GCD test:

If a dependency exists, GCD(c,a) must evenly divide (d-b)

Example:for (i=0; i<100; i=i+1) {X[2*i+3] = X[2*i] * 5.0;}Answer: a=2, b=3, c=2, d=0 GCD(c,a)=2, d-b=-3 no dependence possible.

Reductions

Key Takeaway

SIMD architectures can exploit significant data-level parallelism for:

Matrix-oriented scientific computing

Media-oriented image and sound processors

SIMD is more energy efficient than MIMD

Only needs to fetch one instruction per data operation

Makes SIMD attractive for personal mobile devices

SIMD allows programmer to continue to think sequentially

SIMD Parallelism

Vector architectures

SIMD extensions

5.2 Crosscutting Issues Mobile versus Server GPUs and Tesla versus Core i7

•         Performance: how well scale as increase Proc

•         Speedup fixed as well as scaleup of problem

–        Assume benchmark of size n on p processors makes sense: how scale benchmark to run on m * p processors?

–        Memory-constrained scaling: keeping the amount of memory used per processor constant

–        Time-constrained scaling: keeping total execution time, assuming perfect speedup, constant

•         Example: 1 hour on 10 P, time ~ O(n3), 100 P?

–        Time-constrained scaling: 1 hour, => 101/3n => 2.15n scale up

–        Memory-constrained scaling: 10n size => 103/10 => 100X or 100 hours! 10X processors for 100X longer???

–        Need to know application well to scale: # iterations, error tolerance

•         Multilevel cache hierarchy +  multilevel inclusion—every level of cache hierarchy is a subset of next level—then can reduce contention between coherence traffic and processor traffic

–        Hard if cache blocks different sizes

•         Also issues in memory consistency model and speculation, nonblocking caches, prefetching

Example: Sun Wildfire Prototype

Key Takeaway

•         Performance: how well scale as increase Proc

•         Speedup fixed as well as scaleup of problem

–        Assume benchmark of size n on p processors makes sense: how scale benchmark to run on m * p processors?

–        Memory-constrained scaling: keeping the amount of memory used per processor constant

–        Time-constrained scaling: keeping total execution time, assuming perfect speedup, constant

Text Books:

Reference Books: