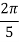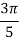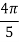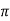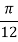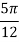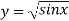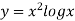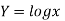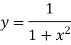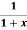Unit – 3
Numerical Integration
In numerical analysis, the Newton-Cotes formulas, also called the Newton-Cotes quadrature rules or simply Newton-Cotes rules, are a group of for numerical integration (also called quadrature) based on evaluating the integrated at equally spaced points. They are named after Isaac Newton and Roger cotes. Newton-cotes formulas can be useful if the value of the integrand at equally spaced points is given. If it is possible to change the points at which the integrands is evaluated, then other methods such as Gaussian quadrature and Clenshaw-Curtis quadrature are probably more suitable.
Note: Suppose that 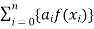 is the n+1 point closed Newton-Cotes formula with
is the n+1 point closed Newton-Cotes formula with 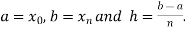 There exists
There exists 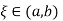 for which n is odd we get:
for which n is odd we get:
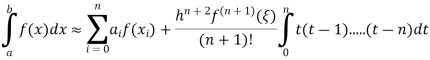
Example 1: Use Simpson’s Rule to approximate the integral of
f(x) = 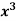 on the interval [1,2].
on the interval [1,2].
Solution:
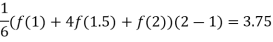
The actual value of the integral is 3.75. This is exact because the error for Simson’s rule is O(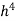 ) and we are integrating a cubic function.
) and we are integrating a cubic function.
Example 2: Use Simpson’s Rule to approximate the integral of
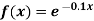 on the interval [2,5].
on the interval [2,5].
Solution:
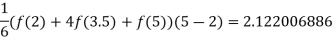
The actual value of the integral is 2.122000934.
Example 3: Suppose we can only evaluate a function at the integers (for example, when we are periodically sampling a signal). Use three applications of Simpson’s rule and two applications of Simpson’s 3/8 Rule to approximate the integral of response with a decaying transient f(x) = cos(x)+x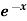 on the interval [0,6].
on the interval [0,6].
Solution:
Thus, we calculate:
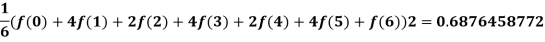
and,
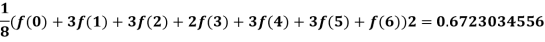
The actual integral is -7exp (-6) + sin (6) +1 = 0.7032332366, and therefore, three applications of Simpson’s rule with intervals of width 2 appears to be more accurate than two applications of Simpson’s 3/8th rule with intervals of width 3.
Example 4: Estimation error of Newton Cotes formula of degree 4.
Solution: From Note (1) we get,
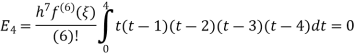
Again, that doesn’t mean that the error is zero. The error term can be obtained from the next term in the Newton Polynomial. i.e.
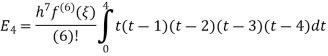
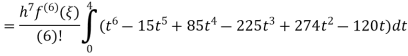
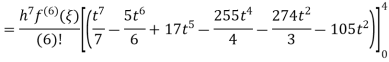
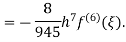
Numerical integration is a process of evaluating or obtaining a definite integral 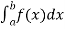 from a set of numerical values of the integrand f(x).In case of function of single variable, the process is called quadrature.
from a set of numerical values of the integrand f(x).In case of function of single variable, the process is called quadrature.
Trapezoidal Method:
Let the interval 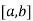 be divided into n equal intervals such that
be divided into n equal intervals such that
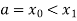 <
<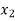 <….<
<….<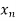 =b.
=b.
Here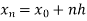 .
.
To find the value of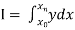 .
.
Setting n=1, we get
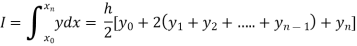
Or I = 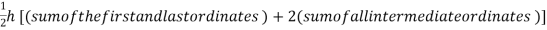
The above is known as Trapezoidal method.
Note: In this method second and higher difference are neglected and so f(x) is a polynomial of degree 1.
Geometrical Significance: The curve y=f(x),is replaced by n straight lines with the points 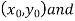 (
(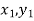 );(
);(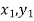 ) and (
) and (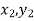 );…….;(
);…….;(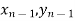 ) and (
) and (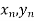 ).
).
The area bounded by the curve y=f(x), the ordinates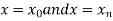 , and the x axis is approximately equivalent to the sum of the area of the n trapeziums obtained.
, and the x axis is approximately equivalent to the sum of the area of the n trapeziums obtained.
Example1: State the trapezoidal rule for finding an approximate area under the given curve. A curve is given by the points (x, y) given below:
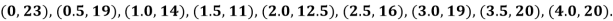
Estimate the area bounded by the curve, the x axis and the extreme ordinates.
We construct the data table:
X | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Y | 23 | 19 | 14 | 11 | 12.5 | 16 | 19 | 20 | 20 |
Here length of interval h =0.5, initial value a = 0 and final value b = 4
By Trapezoidal method
Area of curve bounded on x axis =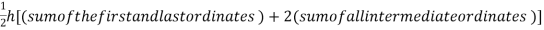
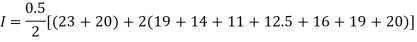
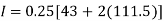
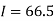
Example2: Compute the value of 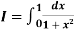 ?
?
Solution: Using the trapezoidal rule with h=0.5, 0.25 and 0.125.
Here 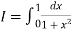
For h=0.5, we construct the data table:
X | 0 | 0.5 | 1 |
Y | 1 | 0.8 | 0.5 |
By Trapezoidal rule
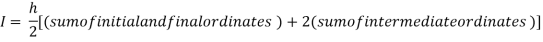
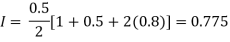
For h=0.25, we construct the data table:
X | 0 | 0.25 | 0.5 | 0.75 | 1 |
Y | 1 | 0.94117 | 0.8 | 0.64 | 0.5 |
By Trapezoidal rule
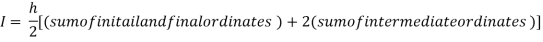
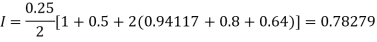
For h = 0.125, we construct the data table:
X | 0 | 0.125 | 0.25 | 0.375 | 0.5 | 0.625 | 0.75 | 0.875 | 1 |
Y | 1 | 0.98461 | 0.94117 | 0.87671 | 0.8 | 0.71910 | 0.64 | 0.56637 | 0.5 |
By Trapezoidal rule
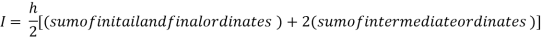
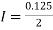 [(1+0.5)+2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
[(1+0.5)+2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
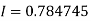
Example3: Evaluate, using trapezoidal rule with five ordinates
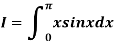
Solution: Here 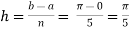
We construct the data table:
X | 0 |
|
|
|
|
|
Y | 0 | 0.3693161 | 1.195328 | 1.7926992 | 1.477265 | 0 |
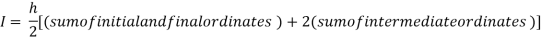
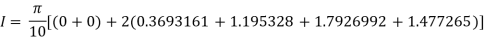
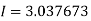
Let the interval  be divided into n equal intervals such that
be divided into n equal intervals such that 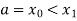 <
<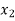 <….<
<….<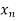 =b.
=b.
Here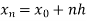 .
.
To find the value of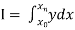 .
.
Setting n = 2,
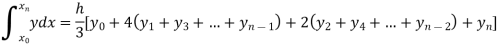
Which is known as Simpson’s 1/3- rule or Simpson’s rule.
Note: In this rule third and higher differences are neglected an so f(x) is a polynomial of degree 2.
Example1: Estimate the value of the integral
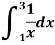
Solution: By Simpson’s rule with 4 strips and 8 strips respectively.
For n=4, we have 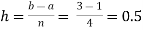
Construct the data table:
X | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
Y=1/x | 1 | 0.66666 | 0.5 | 0.4 | 0.33333 |
By Simpson’s Rule
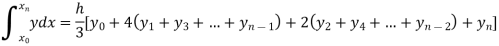
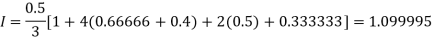
For n = 8, we have 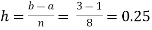
X | 1 | 1.25 | 1.50 | 1.75 | 2.0 | 2.25 | 2.50 | 2.75 | 3.0 |
Y=1/x | 1 | 0.8 | 0.66666 | 0.571428 | 0.5 | 0.444444 | 0.4 | 0.3636363 | 0.333333 |
By Simpson’s Rule
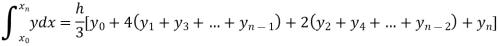
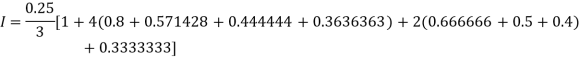
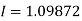
Example2: Evaluate 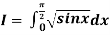
Solution: Using Simpson’s 1/3 rule with 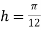 .
.
For 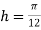 , we construct the data table:
, we construct the data table:
X | 0 |
|
|
|
|
|
|
| 0 | 0.50874 | 0.707106 | 0.840896 | 0.930604 | 0.98281 | 1 |
By Simpson’s Rule
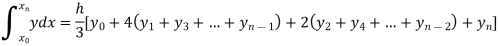
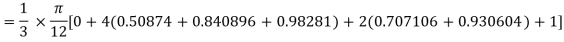
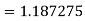
Example3: Using Simpson’s 1/3 rule with h = 1, evaluate 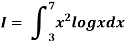
Solution: For h = 1, we construct the data table:
X | 3 | 4 | 5 | 6 | 7 |
| 9.88751 | 22.108709 | 40.23594 | 64.503340 | 95.34959 |
By Simpson’s Rule
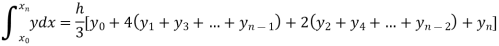
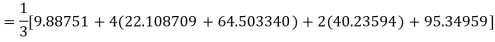
= 177.3853
Let the interval 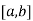 be divided into n equal intervals such that
be divided into n equal intervals such that 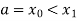 <
<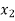 <….<
<….<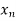 =b.
=b.
Here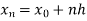 .
.
To find the value of 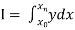 .
.
Setting n=3 , we get
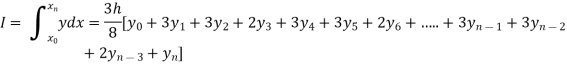
Is known as Simpson’s 3/8 rule which is not as accurate as Simpson’s rule.
Note: In this rule the fourth and higher differences are neglected and so f(x) is a polynomial of degree 3.
Example1: Evaluate 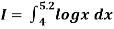
By Simpson’s 3/8 rule.
Let us divide the range of the interval [4, 5.2] into six equal parts.
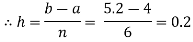
For h=0.2, we construct the data table:
X | 4.0 | 4.2 | 4.4 | 4.6 | 4.8 | 5.0 | 5.2 |
| 1.3863 | 1.4351 | 1.4816 | 1.5261 | 1.5686 | 1.6094 | 1.6487 |
By Simpson’s 3/8 rule
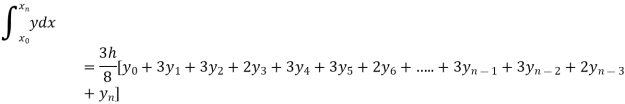

= 1.8278475
Example2: Evaluate 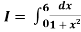
Let us divide the range of the interval [0,6] into six equal parts.
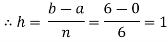
For h=1, we construct the data table:
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 0.5 | 0.2 | 0.1 | 0.0588 | 0.0385 | 0.027 |
By Simpson’s 3/8 rule
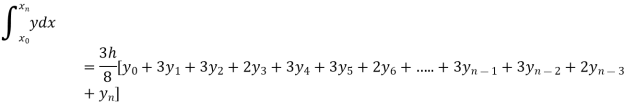
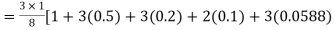 +3(0.0385)+0.027]
+3(0.0385)+0.027]
=1.3571
Error in Simpson’s 3/8 Rule
The error in this rule is given by
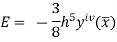
Where 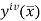 is the largest value of the derivative of y(x).
is the largest value of the derivative of y(x).
Gauss Quadrature 2 point method:
Quadrature: It is the process to evaluate the value of the functions at the chosen point, to its exact value for polynomial up to higher degree as possible.
The general form Gaussian quadrature is given by
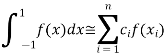
Where 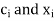 depends on the choice of n (number of points).
depends on the choice of n (number of points).
Also note that the possible polynomial of degree up to 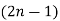 .
.
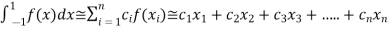 . …..(1)
. …..(1)
For 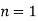 point
point
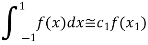
Which gives exact value of the polynomial up to degree 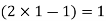 degree
degree
i.e. 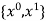
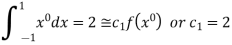
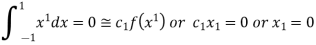
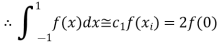
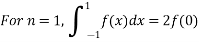
For 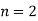 point and using (1)
point and using (1)
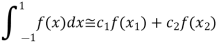
Which gives exact value of the polynomial up to degree 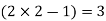 degree
degree
i.e. 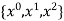
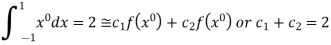
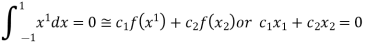
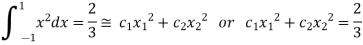
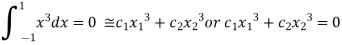
On solving we get
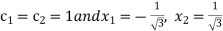 .
.
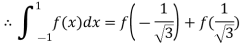
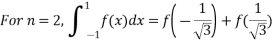
Let the values of a function f(x) be tabulated at points 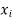 equally spaced by
equally spaced by 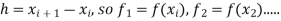 Then Weddle’s rule approximating the integral of f(x) is given by the Newton-Cotes like formula.
Then Weddle’s rule approximating the integral of f(x) is given by the Newton-Cotes like formula.
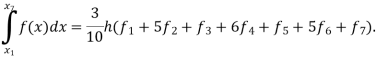
Example 1:
Evaluate:
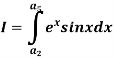
Solution:
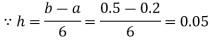
Calculate the values of f(x) = 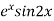
x | 0.2 | 0.25 | 0.3 | 0.35 | 0.4 | 0.45 | 0.5 |
f(x) | 0.475 | 0.165 | 0.716 | 0.914 | 1.070 | 1.228 | 1.387 |
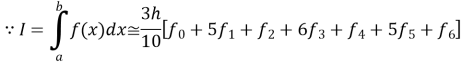
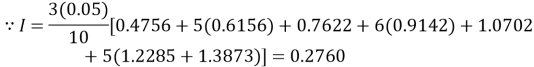
Example 2:
x | 0.25 | 0.5 | 0.75 | 1.0 | 1.25 | 1.5 | 1.75 |
Y= | 0.8 | 0.6666 | 0.5714 | 0.5 | 0.4444 | 0.4 | 0.3636 |
Solution: Weddle’s Rule: It’s a 7-point quadrature formula, i.e. n=6
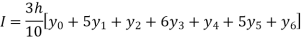
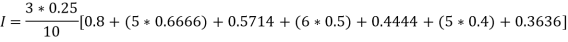
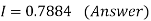
Reference