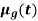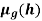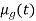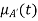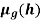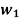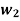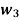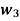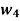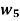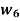Unit – 4
Introduction to Fuzzy sets
4.1 Crisp set and Fuzzy set
Definition Fuzzy set: A fuzzy set is a combination of the elements having a changing degree of memberships in the set. Here “fuzzy” means vagueness, in other words, the transition among various degrees of the membership complies that the limits of the fuzzy sets are vague and ambiguous. Therefore, the membership of the elements from the universe in the set is measured against a function to identify the uncertainty and ambiguity.

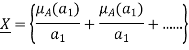
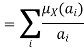
Basis For Comparison:
Basis for comparison | Fuzzy Set | Crisp Set |
Basic | Prescribed by vague or ambiguous properties. | Defined b precise and certain characteristics. |
Property | Elements are allowed to be partially included in the set. | Element is either the member of a set or not.
|
Application | Used in fuzzy controllers | Digital design |
Logic | Infinite-Valued | Bi-valued |
Definition of Crisp Set:
The crisp set is a collection of objects (say U) having identical properties such as countability and finiteness. A crisp set ‘B’ can be defined as a group of elements over the universal set U, where a random element can be a part of B or not. Which means there are only two possible ways, first is the element could belong to set B or it does not belong to set B. The notation to define the crisp set B containing a group of some elements in U having the same property P, is given below.
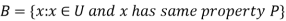
Fuzzy systems:
Example 1: Crisp logic (crisp) is the same as Boolean logic (either 0 or 1). Either a statement is true (1) or it is not (0), mean while fuzzy logic captures the degree to which something is true.
Solution: Consider the statement: “The agreed to met at 12’o clock but ben was not punctual.”
Example 2: Crisp sets versus Fuzzy sets
Crisp set Short average under 170cm tall 170 to 180cm over 180cm |
Characteristic Function
Short ave tall
B | A | C |
| short | ave | tall |
A | 0 | 1 | 0 |
B | 1 | 0 | 0 |
C | 0 | 0 | 1 |
Fuzzy sets: Basic concepts
Example 1:
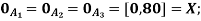
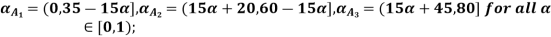
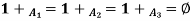
Example 2: A fuzzy set A on R is convex iff A(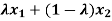 )
)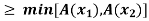
For all 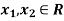 and all
and all 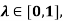 where min denotes the minimum operator.
where min denotes the minimum operator.
Solution: (i) Assume that A is convex and let 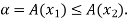 Then
Then 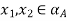 and, moreover,
and, moreover, 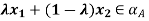 for any
for any 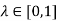 by the convexity o A. Consequently,
by the convexity o A. Consequently,
A (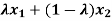 )
)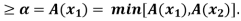
(ii) Assume that a satisfies. We need to prove that for any 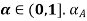 is convex. Now for any
is convex. Now for any 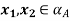 (i.e., A (
(i.e., A (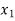 )
) and for any
and for any 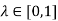
A (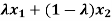 )
)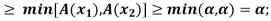
i.e. 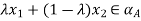 .Therefore,
.Therefore, 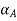 is convex for any
is convex for any 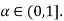 Hence, A is convex.
Hence, A is convex.
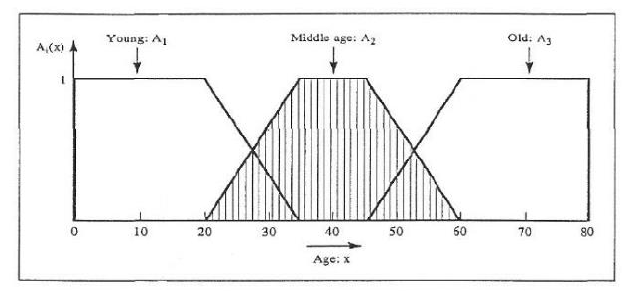
Example 3: Consider three fuzzy sets that represent the concepts of a young middle-aged, and old person. The membership functions are defined on the interval [0,80] as follows:
Solution:

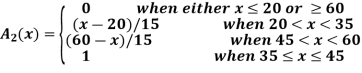

Operation on Fuzzy Sets:
Having two fuzzy sets  , the universe of information U and an element y of the universe, the following relations express the union, intersection and complement operation on fuzzy sets.
, the universe of information U and an element y of the universe, the following relations express the union, intersection and complement operation on fuzzy sets.
Union/Fuzzy ‘OR’
Let us consider the following representation to understand how the Union/Fuzzy ‘OR’ relation works-
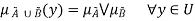
Here 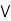 represents the ‘max’ operation.
represents the ‘max’ operation.
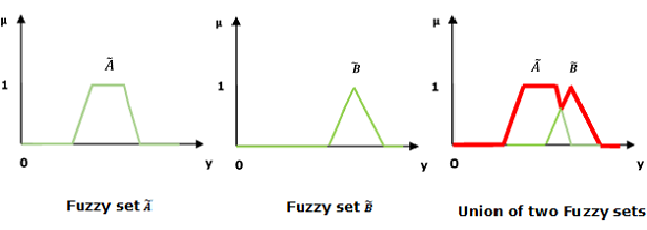
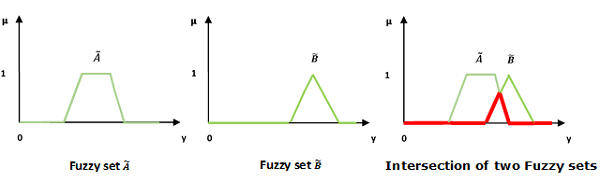
Intersection/Fuzzy ‘AND’
Let us consider the following representation to understand how the Intersection/Fuzzy ‘AND’ relation works-
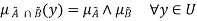
Here 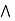 represents the ‘min’ operation.
represents the ‘min’ operation.
Complement/Fuzzy ‘NOT’
Let us consider the following representation to understand how the Complement/Fuzzy ‘NOT’ relation works-
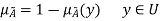
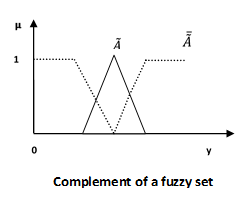
Let us discuss the different properties of fuzzy sets.
Commutative Property:
Having two fuzzy sets 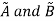 , this property states-
, this property states-
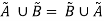
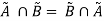
Associative Property:
Having three fuzzy sets 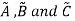 this property states-
this property states-
Distributive Property:
Having three fuzzy sets 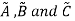 this property states-
this property states-
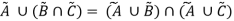
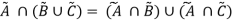
Idempotency Property:
For any fuzzy set 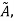 this property states-
this property states-
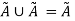
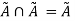
Identity Property:
For fuzzy set 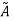 and universal set U, this property states-
and universal set U, this property states-
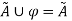
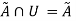
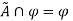
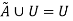
Transitive Property:
Having three fuzzy sets 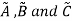 , this property states-
, this property states-
If 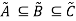 , then
, then 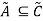
Involution Property:
For any fuzzy set 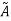 , this property states-
, this property states-
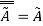
De Morgan’s Law:
This law plays a crucial role in proving tautologies and contradiction. This law states-
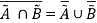
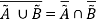
Some Solved Examples:
Example 1:
t | 20 | 30 | 40 |
| 0.1 | 0.5 | 0.9 |
h | 20 | 50 | 70 | 90 |
| 0.2 | 0.6 | 0.7 | 1 |
| 20 | 50 | 70 | 90 |
20 | 0.1 | 0.1 | 0.1 | 0.1 |
30 | 0.2 | 0.5 | 0.5 | 0.5 |
40 | 0.2 | 0.6 | 0.7 | 0.9 |
Calculated R (t,h) through min operator
Solution: Now suppose, we want to get information about the humidity when there is the following premise about the temperature:
Temperature is fairly high.
This fact is rewritten as R(t): t is 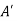 where
where 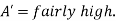
Where the fuzzy term 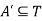 is defined as below membership function of
is defined as below membership function of 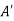 in T (temperature)
in T (temperature)
t | 20 | 30 | 40 |
| 0.01 | 0.25 | 0.81 |
R(h)= R(t) o R(t,h)
| 20 | 50 | 70 | 90 |
20 | 0.1 | 0.1 | 0.1 | 0.1 |
30 | 0.2 | 0.5 | 0.5 | 0.5 |
40 | 0.2 | 0.6 | 0.7 | 0.9 |
t | 20 | 30 | 40 |
| 0.01 | 0.25 | 0.81 |
h | 20 | 50 | 70 | 90 |
| 0.2 | 0.6 | 0.7 | 0.81 |
Example 2: Let P = {paris, berlin, Amsterdam} and Q = {Rome, Madrid, Lisbon} be two set of cities, and E = {far, very far, near, very near}. Let R be the fuzzy soft relation over the sets P and Q given by (R,E) = {R(for) = {(paris, Rome)/0.60, (paris, madrid/ 0.45, (Paris, Lisbon)/0.40, (Berlin, Rome)/ 0.50, (Berlin, Madrid)/0.65), (Berlin, Lisbon)/0.70,(Amsterdam, Rome)/0.75, (Amsterdam, Madrid)/0.50,(Amsterdam, Lisbon)/0.80}}.This information can be represented in the form of two-dimensional array(matrix) as shown in the Table 4. It is obvious from the matrix given in table 4 that a fuzzy soft relation may be considered as a parameterized fuzzy relation.
Solution:
(1) Union: 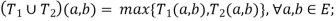
(2) Intersection: 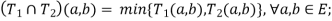
(3) Containment: 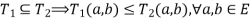
R(far) | Rome | Madrid | Lisbon |
Paris | 0.60 | 0.45 | 0.40 |
Berlin | 0.55 | 0.65 | 0.70 |
Amsterdam | 0.75 | 0.50 | 0.80 |
Example 3: Let U = { } be the set of watches and A = {cheap, costly}, B = {Beautiful, in a golden locket}. Let (F, A) and (G,B) be two soft sets given by F (cheap) = {
} be the set of watches and A = {cheap, costly}, B = {Beautiful, in a golden locket}. Let (F, A) and (G,B) be two soft sets given by F (cheap) = { .The relation
.The relation 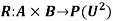 is given by the following membership matrices in table 5 and 6. The membership function of R can also be defined using other appropriate techniques.
is given by the following membership matrices in table 5 and 6. The membership function of R can also be defined using other appropriate techniques.
Solution:
R(Costly beautiful) |
|
|
|
|
|
|
| 0.65 | 1 | 0.80 | 0.70 | 0.80 | 0.75 |
| 0.49 | 0.75 | 0.60 | 0.53 | 0.60 | 0.56 |
| 0.52 | 0.80 | 0.64 | 0.56 | 0.64 | 0.60 |
| 0.35 | 0.55 | 0.44 | 0.39 | 0.55 | 0.42 |
| 0.59 | 0.90 | 0.72 | 0.63 | 0.72 | 0.68 |
| 0.53 | 0.85 | 0.68 | 0.60 | 0.68 | 0.64 |
Reference