UNIT- 1

Basic of Data Structures

1.1 Data structure- Definition, Types of data structures, Data Structure Operations

Introduction

Data Structure can be defined as the group of data elements which provides an efficient way of storing and organising data in the computer so that it can be used efficiently. Some examples of Data Structures are arrays, Linked List, Stack, Queue, etc. Data Structures are widely used in almost every aspect of Computer Science i.e. operating System, Compiler Design, Artificial intelligence, Graphics and many more.

Data Structures are the main part of many computer science algorithms as they enable the programmers to handle the data in an efficient way. It plays a vital role in enhancing the performance of software or a program as the main function of the software is to store and retrieve the user's data as fast as possible

Basic Terminology

Data structures are the building blocks of any program or the software. Choosing the appropriate data structure for a program is the most difficult task for a programmer. Following terminology is used as far as data structures are concerned

Data: Data can be defined as an elementary value or the collection of values, for example, student's name and its id are the data about the student.

Group Items: Data items which have subordinate data items are called Group item, for example, name of a student can have first name and the last name.

Record: Record can be defined as the collection of various data items, for example, if we talk about the student entity, then its name, address, course and marks can be grouped together to form the record for the student.

File: A File is a collection of various records of one type of entity, for example, if there are 60 employees in the class, then there will be 20 records in the related file where each record contains the data about each employee.

Attribute and Entity: An entity represents the class of certain objects. it contains various attributes. Each attribute represents the particular property of that entity.

Field: Field is a single elementary unit of information representing the attribute of an entity.

Need of Data Structures

As applications are getting complexed and amount of data is increasing day by day, there may arise the following problems:

Processor speed: To handle very large amount of data, high speed processing is required, but as the data is growing day by day to the billions of files per entity, processor may fail to deal with that much amount of data.

Data Search: Consider an inventory size of 106 items in a store, If our application needs to search for a particular item, it needs to traverse 106 items every time, results in slowing down the search process.

Multiple requests: If thousands of users are searching the data simultaneously on a web server, then there are the chances that a very large server can be failed during that process

In order to solve the above problems, data structures are used. Data is organized to form a data structure in such a way that all items are not required to be searched and required data can be searched instantly.

Advantages of Data Structures

Efficiency: Efficiency of a program depends upon the choice of data structures. For example: suppose, we have some data and we need to perform the search for a particular record. In that case, if we organize our data in an array, we will have to search sequentially element by element. Hence, using array may not be very efficient here. There are better data structures which can make the search process efficient like ordered array, binary search tree or hash tables.

Reusability: Data structures are reusable, i.e. once we have implemented a particular data structure, we can use it at any other place. Implementation of data structures can be compiled into libraries which can be used by different clients.

Abstraction: Data structure is specified by the ADT which provides a level of abstraction. The client program uses the data structure through interface only, without getting into the implementation details.

Data Structure Classification

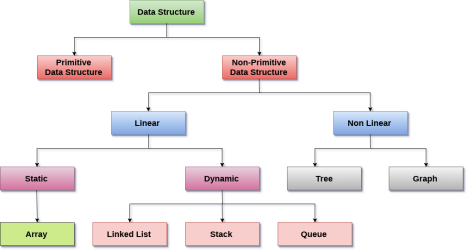
Linear Data Structures: A data structure is called linear if all of its elements are arranged in the linear order. In linear data structures, the elements are stored in non-hierarchical way where each element has the successors and predecessors except the first and last element.

Types of Linear Data Structures are given below:

Arrays: An array is a collection of similar type of data items and each data item is called an element of the array. The data type of the element may be any valid data type like char, int, float or double.

The elements of array share the same variable name but each one carries a different index number known as subscript. The array can be one dimensional, two dimensional or multidimensional.

The individual elements of the array age are:

Age [0], age[1], age[2], age[3],......... age[98], age[99].

Linked List: Linked list is a linear data structure which is used to maintain a list in the memory. It can be seen as the collection of nodes stored at non-contiguous memory locations. Each node of the list contains a pointer to its adjacent node.

Stack: Stack is a linear list in which insertion and deletions are allowed only at one end, called top.

A stack is an abstract data type (ADT), can be implemented in most of the programming languages. It is named as stack because it behaves like a real-world stack, for example: - piles of plates or deck of cards etc.

Queue: Queue is a linear list in which elements can be inserted only at one end called rear and deleted only at the other end called front.

It is an abstract data structure, similar to stack. Queue is opened at both end therefore it follows First-In-First-Out (FIFO) methodology for storing the data items.

Non Linear Data Structures: This data structure does not form a sequence i.e. each item or element is connected with two or more other items in a non-linear arrangement. The data elements are not arranged in sequential structure.

Types of Non Linear Data Structures are given below:

Trees: Trees are multilevel data structures with a hierarchical relationship among its elements known as nodes. The bottommost nodes in the herierchy are called leaf node while the topmost node is called root node. Each node contains pointers to point adjacent nodes.

Tree data structure is based on the parent-child relationship among the nodes. Each node in the tree can have more than one child except the leaf nodes whereas each node can have atmost one parent except the root node. Trees can be classified into many categories which will be discussed later in this tutorial.

Graphs: Graphs can be defined as the pictorial representation of the set of elements (represented by vertices) connected by the links known as edges. A graph is different from tree in the sense that a graph can have cycle while the tree cannot have the one.

Operations on data structure

1) Traversing: Every data structure contains the set of data elements. Traversing the data structure means visiting each element of the data structure in order to perform some specific operation like searching or sorting.

Example: If we need to calculate the average of the marks obtained by a student in 6 different subject. We need to traverse the complete array of marks and calculate the total sum then, we will divide that sum by the number of subjects i.e. 6, in order to find the average.

2) Insertion: Insertion can be defined as the process of adding the elements to the data structure at any location.

If the size of data structure is n then we can only insert n-1 data elements into it.

3) Deletion: The process of removing an element from the data structure is called Deletion. We can delete an element from the data structure at any random location.

If we try to delete an element from an empty data structure then underflow occurs.

4) Searching: The process of finding the location of an element within the data structure is called Searching. There are two algorithms to perform searching, Linear Search and Binary Search. We will discuss each one of them later in this tutorial.

5) Sorting: The process of arranging the data structure in a specific order is known as Sorting. There are many algorithms that can be used to perform sorting, for example, insertion sort, selection sort, bubble sort, etc.

6) Merging: When two lists List A and List B of size M and N respectively, of similar type of elements, clubbed or joined to produce the third list, List C of size (M+N), then this process is called merging

1.2 Algorithms: Complexity, Time and Space complexity

What is an Algorithm?

An algorithm is a process or a set of rules required to perform calculations or some other problem-solving operations especially by a computer. The formal definition of an algorithm is that it contains the finite set of instructions which are being carried in a specific order to perform the specific task. It is not the complete program or code; it is just a solution (logic) of a problem, which can be represented either as an informal description using a Flowchart or Pseudocode.

Characteristics of an Algorithm

The following are the characteristics of an algorithm:

Dataflow of an Algorithm

Why do we need Algorithms?

We need algorithms because of the following reasons:

Let's understand the algorithm through a real-world example. Suppose we want to make a lemon juice, so following are the steps required to make a lemon juice:

Step 1: First, we will cut the lemon into half.

Step 2: Squeeze the lemon as much you can and take out its juice in a container.

Step 3: Add two tablespoon sugar in it.

Step 4: Stir the container until the sugar gets dissolved.

Step 5: When sugar gets dissolved, add some water and ice in it.

Step 6: Store the juice in a fridge for 5 to minutes.

Step 7: Now, it's ready to drink.

The above real-world can be directly compared to the definition of the algorithm. We cannot perform the step 3 before the step 2, we need to follow the specific order to make lemon juice. An algorithm also says that each and every instruction should be followed in a specific order to perform a specific task.

Now we will look an example of an algorithm in programming.

We will write an algorithm to add two numbers entered by the user.

The following are the steps required to add two numbers entered by the user:

Step 1: Start

Step 2: Declare three variables a, b, and sum.

Step 3: Enter the values of a and b.

Step 4: Add the values of a and b and store the result in the sum variable, i.e., sum=a+b.

Step 5: Print sum

Step 6: Stop

Factors of an Algorithm

The following are the factors that we need to consider for designing an algorithm:

Importance of Algorithms

Issues of Algorithms

The following are the issues that come while designing an algorithm:

Approaches of Algorithm

The following are the approaches used after considering both the theoretical and practical importance of designing an algorithm:

The major categories of algorithms are given below:

Algorithm Analysis

The algorithm can be analyzed in two levels, i.e., first is before creating the algorithm, and second is after creating the algorithm. The following are the two analysis of an algorithm:

Algorithm Complexity

The performance of the algorithm can be measured in two factors:

In the above code, the time complexity of the loop statement will be atleast n, and if the value of n increases, then the time complexity also increases. While the complexity of the code, i.e., return sum will be constant as its value is not dependent on the value of n and will provide the result in one step only. We generally consider the worst-time complexity as it is the maximum time taken for any given input size.

For an algorithm, the space is required for the following purposes:

Auxiliary space: The extra space required by the algorithm, excluding the input size, is known as an auxiliary space. The space complexity considers both the spaces, i.e., auxiliary space, and space used by the input.

So,

Space complexity = Auxiliary space + Input size.

Types of Algorithms

The following are the types of algorithm:

Search Algorithm

On each day, we search for something in our day to day life. Similarly, with the case of computer, huge data is stored in a computer that whenever the user asks for any data then the computer searches for that data in the memory and provides that data to the user. There are mainly two techniques available to search the data in an array:

Linear Search

Linear search is a very simple algorithm that starts searching for an element or a value from the beginning of an array until the required element is not found. It compares the element to be searched with all the elements in an array, if the match is found, then it returns the index of the element else it returns -1. This algorithm can be implemented on the unsorted list.

Binary Search

A Binary algorithm is the simplest algorithm that searches the element very quickly. It is used to search the element from the sorted list. The elements must be stored in sequential order or the sorted manner to implement the binary algorithm. Binary search cannot be implemented if the elements are stored in a random manner. It is used to find the middle element of the list.

Sorting Algorithms

Sorting algorithms are used to rearrange the elements in an array or a given data structure either in an ascending or descending order. The comparison operator decides the new order of the elements.

Why do we need a sorting algorithm?

Time and Space Complexity in Data Structure

Algorithm Analysis

Analysis of efficiency of an algorithm can be performed at two different stages, before implementation and after implementation, as

A priori analysis −This is defined as theoretical analysis of an algorithm. Efficiency of algorithm is measured by assuming that all other factors e.g. speed of processor, are constant and have no effect on implementation.

A posterior analysis −This is defined as empirical analysis of an algorithm. The chosen algorithm is implemented using programming language. Next the chosen algorithm is executed on target computer machine. In this analysis, actual statistics like running time and space needed are collected.

Algorithm analysis is dealt with the execution or running time of various operations involved. Running time of an operation can be defined as number of computer instructions executed per operation.

Algorithm Complexity

Suppose X is treated as an algorithm and N is treated as the size of input data, the time and space implemented by the Algorithm X are the two main factors which determine the efficiency of X.

Time Factor −The time is calculated or measured by counting the number of key operations such as comparisons in sorting algorithm.

Space Factor −The space is calculated or measured by counting the maximum memory space required by the algorithm.

The complexity of an algorithm f(N) provides the running time and / or storage space needed by the algorithm with respect of N as the size of input data.

Space Complexity

Space complexity of an algorithm represents the amount of memory space needed the algorithm in its life cycle.

Space needed by an algorithm is equal to the sum of the following two components

A fixed part that is a space required to store certain data and variables (i.e. simple variables and constants, program size etc.), that are not dependent of the size of the problem.

A variable part is a space required by variables, whose size is totally dependent on the size of the problem. For example, recursion stack space, dynamic memory allocation etc.

Space complexity S(p) of any algorithm p is S(p) = A + Sp(I) Where A is treated as the fixed part and S(I) is treated as the variable part of the algorithm which depends on instance characteristic I. Following is a simple example that tries to explain the concept

Algorithm

SUM(P, Q)

Step 1 - START

Step 2 - R ← P + Q + 10

Step 3 - Stop

Here we have three variables P, Q and R and one constant. Hence S(p) = 1+3. Now space is dependent on data types of given constant types and variables and it will be multiplied accordingly.

Time Complexity

Time Complexity of an algorithm is the representation of the amount of time required by the algorithm to execute to completion. Time requirements can be denoted or defined as a numerical function t(N), where t(N) can be measured as the number of steps, provided each step takes constant time.

For example, in case of addition of two n-bit integers, N steps are taken. Consequently, the total computational time is t(N) = c*n, where c is the time consumed for addition of two bits. Here, we observe that t(N) grows linearly as input size increases.

TEXT BOOKS:

REFERENCE BOOKS: