UNIT- 3
Stacks and Queues
Stack
Stack is an ordered list in which, insertion and deletion can be performed only at one end that is called top.
Applications of Stack
Operations on Stack
There are various operations which can be performed on stack.
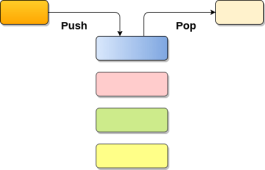
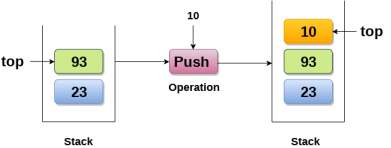
1. Push : Adding an element onto the stack
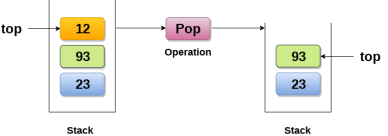
2. Pop : Removing an element from the stack
3. Peek: Look all the elements of stack without removing them.
How the stack grows?
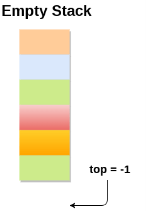
Scenario 1: Stack is empty
The stack is called empty if it doesn't contain any element inside it. At this stage, the value of variable top is -1.
Scenario 2: Stack is not empty
Value of top will get increased by 1 every time when we add any element to the stack. In the following stack, After adding first element, top = 2.
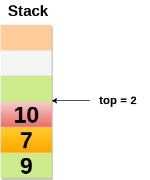
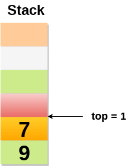
Scenario 3: Deletion of an element
Value of top will get decreased by 1 whenever an element is deleted from the stack.
In the following stack, after deleting 10 from the stack, top = 1.
Top and its value:
Top position | Status of stack |
-1 | Empty |
0 | Only one element in the stack |
N-1 | Stack is full |
N | Overflow |
Array implementation of Stack
In array implementation, the stack is formed by using the array. All the operations regarding the stack are performed using arrays. Lets see how each operation can be implemented on the stack using array data structure.
Adding an element onto the stack (push operation)
Adding an element into the top of the stack is referred to as push operation. Push operation involves following two steps.
Stack is overflown when we try to insert an element into a completely filled stack therefore, our main function must always avoid stack overflow condition.
Algorithm:
Time Complexity: o(1)
Implementation of push algorithm in C language
Deletion of an element from a stack (Pop operation)
Deletion of an element from the top of the stack is called pop operation. The value of the variable top will be incremented by 1 whenever an item is deleted from the stack. The top most element of the stack is stored in an another variable and then the top is decremented by 1. The operation returns the deleted value that was stored in another variable as the result.
The underflow condition occurs when we try to delete an element from an already empty stack.
Algorithm:
Time Complexity : o(1)
Implementation of POP algorithm using C language
Visiting each element of the stack (Peek operation)
Peek operation involves returning the element which is present at the top of the stack without deleting it. Underflow condition can occur if we try to return the top element in an already empty stack.
Algorithm :
PEEK (STACK, TOP)
Time complexity: o(n)
Implementation of Peek algorithm in C language
C program
Java Program
C# Program
Linked list implementation of stack
Instead of using array, we can also use linked list to implement stack. Linked list allocates the memory dynamically. However, time complexity in both the scenario is same for all the operations i.e. push, pop and peek.
In linked list implementation of stack, the nodes are maintained non-contiguously in the memory. Each node contains a pointer to its immediate successor node in the stack. Stack is said to be overflown if the space left in the memory heap is not enough to create a node.
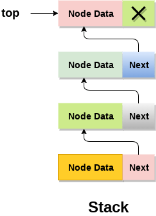
The top most node in the stack always contains null in its address field. Lets discuss the way in which, each operation is performed in linked list implementation of stack.
Adding a node to the stack (Push operation)
Adding a node to the stack is referred to as push operation. Pushing an element to a stack in linked list implementation is different from that of an array implementation. In order to push an element onto the stack, the following steps are involved.
Time Complexity : o(1)
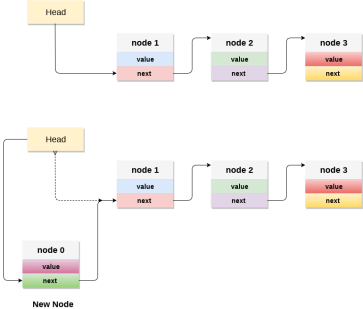
C implementation :
Deleting a node from the stack (POP operation)
Deleting a node from the top of stack is referred to as pop operation. Deleting a node from the linked list implementation of stack is different from that in the array implementation. In order to pop an element from the stack, we need to follow the following steps :
30. Check for the underflow condition: The underflow condition occurs when we try to pop from an already empty stack. The stack will be empty if the head pointer of the list points to null.
31. Adjust the head pointer accordingly: In stack, the elements are popped only from one end, therefore, the value stored in the head pointer must be deleted and the node must be freed. The next node of the head node now becomes the head node.
Time Complexity : o(n)
C implementation
Display the nodes (Traversing)
Displaying all the nodes of a stack needs traversing all the nodes of the linked list organized in the form of stack. For this purpose, we need to follow the following steps.
19. Copy the head pointer into a temporary pointer.
20. Move the temporary pointer through all the nodes of the list and print the value field attached to every node.
Time Complexity : o(n)
C Implementation
Menu Driven program in C implementing all the stack operations using linked list :
Queue
1. A queue can be defined as an ordered list which enables insert operations to be performed at one end called REAR and delete operations to be performed at another end called FRONT.
2. Queue is referred to be as First In First Out list.
3. For example, people waiting in line for a rail ticket form a queue.

Applications of Queue
Due to the fact that queue performs actions on first in first out basis which is quite fair for the ordering of actions. There are various applications of queues discussed as below.
Complexity
Data Structure | Time Complexity | Space Compleity | |||||||
| Average | Worst | Worst | ||||||
| Access | Search | Insertion | Deletion | Access | Search | Insertion | Deletion |
|
Queue | θ(n) | θ(n) | θ(1) | θ(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
Array representation of Queue
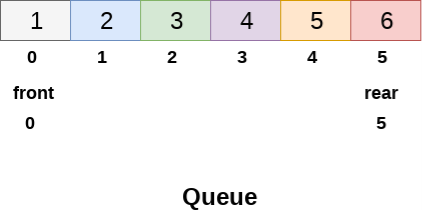
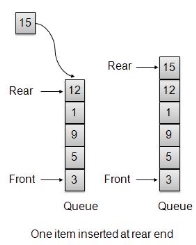
We can easily represent queue by using linear arrays. There are two variables i.e. front and rear that are implemented in the case of every queue. Front and rear variables point to the position from where insertions and deletions are performed in a queue. Initially, the value of front and queue is -1 which represents an empty queue. Array representation of a queue containing 5 elements along with the respective values of front and rear, is shown in the following figure.
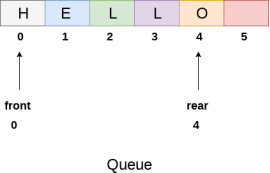
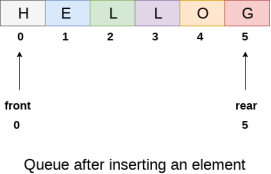
The above figure shows the queue of characters forming the English word "HELLO". Since, No deletion is performed in the queue till now, therefore the value of front remains -1 . However, the value of rear increases by one every time an insertion is performed in the queue. After inserting an element into the queue shown in the above figure, the queue will look something like following. The value of rear will become 5 while the value of front remains same.
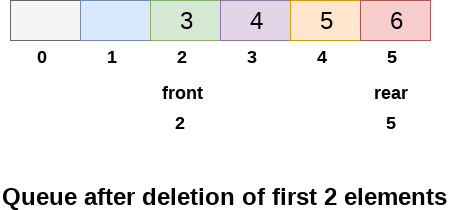
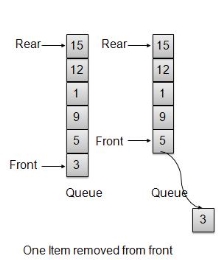
After deleting an element, the value of front will increase from -1 to 0. however,
the queue will look something like following. 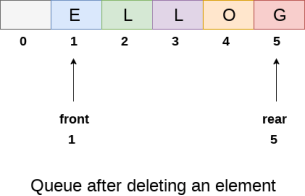
Algorithm to insert any element in a queue
Check if the queue is already full by comparing rear to max - 1. if so, then return an overflow error.
If the item is to be inserted as the first element in the list, in that case set the value of front and rear to 0 and insert the element at the rear end.
Otherwise keep increasing the value of rear and insert each element one by one having rear as the index.
Algorithm
Write OVERFLOW
Go to step
[END OF IF]
SET FRONT = REAR = 0
ELSE
SET REAR = REAR + 1
[END OF IF]
C Function
Algorithm to delete an element from the queue
If, the value of front is -1 or value of front is greater than rear , write an underflow message and exit.
Otherwise, keep increasing the value of front and return the item stored at the front end of the queue at each time.
Algorithm
Write UNDERFLOW
ELSE
SET VAL = QUEUE[FRONT]
SET FRONT = FRONT + 1
[END OF IF]
C Function
Menu driven program to implement queue using array
Output:
*************Main Menu**************
==============================================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?1
Enter the element
123
Value inserted
*************Main Menu**************
==============================================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?1
Enter the element
90
Value inserted
*************Main Menu**************
===================================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?2
value deleted
*************Main Menu**************
==============================================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?3
printing values .....
90
*************Main Menu**************
==============================================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?4
Drawback of array implementation
Although, the technique of creating a queue is easy, but there are some drawbacks of using this technique to implement a queue.
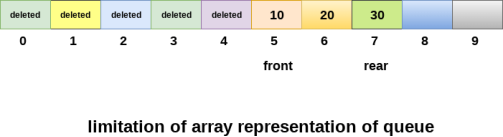
The above figure shows how the memory space is wasted in the array representation of queue. In the above figure, a queue of size 10 having 3 elements is shown. The value of the front variable is 5, therefore, we cannot reinsert the values in the place of already deleted element before the position of front. That much space of the array is wasted and cannot be used in the future (for this queue).
On of the most common problem with array implementation is the size of the array which requires to be declared in advance. Due to the fact that, the queue can be extended at runtime depending upon the problem, the extension in the array size is a time taking process and almost impossible to be performed at runtime since a lot of reallocations take place. Due to this reason, we can declare the array large enough so that we can store queue elements as enough as possible but the main problem with this declaration is that, most of the array slots (nearly half) can never be reused. It will again lead to memory wastage.
Linked List implementation of Queue
Due to the drawbacks discussed in the previous section of this tutorial, the array implementation can not be used for the large scale applications where the queues are implemented. One of the alternative of array implementation is linked list implementation of queue.
The storage requirement of linked representation of a queue with n elements is o(n) while the time requirement for operations is o(1).
In a linked queue, each node of the queue consists of two parts i.e. data part and the link part. Each element of the queue points to its immediate next element in the memory.
In the linked queue, there are two pointers maintained in the memory i.e. front pointer and rear pointer. The front pointer contains the address of the starting element of the queue while the rear pointer contains the address of the last element of the queue.
Insertion and deletions are performed at rear and front end respectively. If front and rear both are NULL, it indicates that the queue is empty.
The linked representation of queue is shown in the following figure.
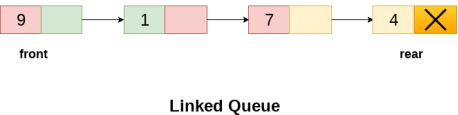
Operation on Linked Queue
There are two basic operations which can be implemented on the linked queues. The operations are Insertion and Deletion.
Insert operation
The insert operation append the queue by adding an element to the end of the queue. The new element will be the last element of the queue.
Firstly, allocate the memory for the new node ptr by using the following statement.
There can be the two scenario of inserting this new node ptr into the linked queue.
In the first scenario, we insert element into an empty queue. In this case, the condition front = NULL becomes true. Now, the new element will be added as the only element of the queue and the next pointer of front and rear pointer both, will point to NULL.
In the second case, the queue contains more than one element. The condition front = NULL becomes false. In this scenario, we need to update the end pointer rear so that the next pointer of rear will point to the new node ptr. Since, this is a linked queue, hence we also need to make the rear pointer point to the newly added node ptr. We also need to make the next pointer of rear point to NULL.
In this way, the element is inserted into the queue. The algorithm and the C implementation is given as follows.
Algorithm
SET FRONT = REAR = PTR
SET FRONT -> NEXT = REAR -> NEXT = NULL
ELSE
SET REAR -> NEXT = PTR
SET REAR = PTR
SET REAR -> NEXT = NULL
[END OF IF]
C Function
Deletion
Deletion operation removes the element that is first inserted among all the queue elements. Firstly, we need to check either the list is empty or not. The condition front == NULL becomes true if the list is empty, in this case , we simply write underflow on the console and make exit.
Otherwise, we will delete the element that is pointed by the pointer front. For this purpose, copy the node pointed by the front pointer into the pointer ptr. Now, shift the front pointer, point to its next node and free the node pointed by the node ptr. This is done by using the following statements.
The algorithm and C function is given as follows.
Algorithm
Write " Underflow "
Go to Step 5
[END OF IF]
C Function
Menu-Driven Program implementing all the operations on Linked Queue
Output:
***********Main Menu**********
==============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?1
Enter value?
123
***********Main Menu**********
==============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?1
Enter value?
90
***********Main Menu**********
==============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?3
printing values .....
123
90
***********Main Menu**********
==============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?2
***********Main Menu**********
==============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?3
printing values .....
90
***********Main Menu**********
==============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?4
Circular Queue
Deletions and insertions can only be performed at front and rear end respectively, as far as linear queue is concerned.
Consider the queue shown in the following figure.
The Queue shown in above figure is completely filled and there can't be inserted any more element due to the condition rear == max - 1 becomes true.
However, if we delete 2 elements at the front end of the queue, we still can not insert any element since the condition rear = max -1 still holds.
This is the main problem with the linear queue, although we have space available in the array, but we can not insert any more element in the queue. This is simply the memory wastage and we need to overcome this problem.
One of the solution of this problem is circular queue. In the circular queue, the first index comes right after the last index. You can think of a circular queue as shown in the following figure.
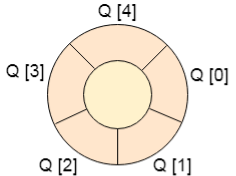
Circular queue will be full when front = -1 and rear = max-1. Implementation of circular queue is similar to that of a linear queue. Only the logic part that is implemented in the case of insertion and deletion is different from that in a linear queue.
Complexity
Time Complexity
Front | O(1) |
Rear | O(1) |
enQueue() | O(1) |
deQueue() | O(1) |
Insertion in Circular queue
There are three scenario of inserting an element in a queue.
Algorithm to insert an element in circular queue
Write " OVERFLOW "
Goto step 4
[End OF IF]
SET FRONT = REAR = 0
ELSE IF REAR = MAX - 1 and FRONT ! = 0
SET REAR = 0
ELSE
SET REAR = (REAR + 1) % MAX
[END OF IF]
C Function
Algorithm to delete an element from a circular queue
To delete an element from the circular queue, we must check for the three following conditions.
Algorithm
Write " UNDERFLOW "
Goto Step 4
[END of IF]
SET FRONT = REAR = -1
ELSE
IF FRONT = MAX -1
SET FRONT = 0
ELSE
SET FRONT = FRONT + 1
[END of IF]
[END OF IF]
C Function
Menu-Driven program implementing all the operations on a circular queue
Output:
**********Main Menu**********
=============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?1
Enter the element
1
Value inserted
**********Main Menu**********
=============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?1
Enter the element
2
Value inserted
**********Main Menu**********
=============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?1
Enter the element
3
Value inserted
**********Main Menu**********
=============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?3
Circular Queue Elements are :
1
2
3
**********Main Menu**********
=============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?2
**********Main Menu**********
=============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?1
Enter the element
4
Value inserted
**********Main Menu**********
=============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?3
Circular Queue Elements are :
2
3
4
**********Main Menu**********
=============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?1
Enter the element
1
OVERFLOW
**********Main Menu**********
=============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?
4
Priority Queue
Overview
Priority Queue is more specialized data structure than Queue. Like ordinary queue, priority queue has same method but with a major difference. In Priority queue items are ordered by key value so that item with the lowest value of key is at front and item with the highest value of key is at rear or vice versa. So we're assigned priority to item based on its key value. Lower the value, higher the priority. Following are the principal methods of a Priority Queue.
Basic Operations
Priority Queue Representation
We're going to implement Queue using array in this article. There is few more operations supported by queue which are following.
Insert / Enqueue Operation
Whenever an element is inserted into queue, priority queue inserts the item according to its order. Here we're assuming that data with high value has low priority.
void insert(int data){
inti = 0;
if(!isFull()){
// if queue is empty, insert the data
if(itemCount == 0){
intArray[itemCount++] = data;
}else{
// start from the right end of the queue
for(i = itemCount - 1; i>= 0; i-- ){
// if data is larger, shift existing item to right end
if(data >intArray[i]){
intArray[i+1] = intArray[i];
}else{
break;
}
}
// insert the data
intArray[i+1] = data;
itemCount++;
}
}
}
Remove / Dequeue Operation
Whenever an element is to be removed from queue, queue get the element using item count. Once element is removed. Item count is reduced by one.
intremoveData(){
returnintArray[--itemCount];
}
Demo Program
PriorityQueueDemo.c
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
intintArray[MAX];
intitemCount = 0;
int peek(){
returnintArray[itemCount - 1];
}
boolisEmpty(){
returnitemCount == 0;
}
boolisFull(){
returnitemCount == MAX;
}
int size(){
returnitemCount;
}
void insert(int data){
inti = 0;
if(!isFull()){
// if queue is empty, insert the data
if(itemCount == 0){
intArray[itemCount++] = data;
}else{
// start from the right end of the queue
for(i = itemCount - 1; i>= 0; i-- ){
// if data is larger, shift existing item to right end
if(data >intArray[i]){
intArray[i+1] = intArray[i];
}else{
break;
}
}
// insert the data
intArray[i+1] = data;
itemCount++;
}
}
}
intremoveData(){
returnintArray[--itemCount];
}
int main() {
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
// ------------------
// index : 0 1 2 3 4
// ------------------
// queue : 12 9 5 3 1
insert(15);
// ---------------------
// index : 0 1 2 3 4 5
// ---------------------
// queue : 15 12 9 5 3 1
if(isFull()){
printf("Queue is full!\n");
}
// remove one item
intnum = removeData();
printf("Element removed: %d\n",num);
// ---------------------
// index : 0 1 2 3 4
// ---------------------
// queue : 15 12 9 5 3
// insert more items
insert(16);
// ----------------------
// index : 0 1 2 3 4 5
// ----------------------
// queue : 16 15 12 9 5 3
// As queue is full, elements will not be inserted.
insert(17);
insert(18);
// ----------------------
// index : 0 1 2 3 4 5
// ----------------------
// queue : 16 15 12 9 5 3
printf("Element at front: %d\n",peek());
printf("----------------------\n");
printf("index : 5 4 3 2 1 0\n");
printf("----------------------\n");
printf("Queue: ");
while(!isEmpty()){
int n = removeData();
printf("%d ",n);
}
}
If we compile and run the above program then it would produce following result −
Queue is full!
Element removed: 1
Element at front: 3
----------------------
index : 5 4 3 2 1 0
----------------------
Queue: 3 5 9 12 15 16
Deque
The dequeue stands for Double Ended Queue. In the queue, the insertion takes place from one end while the deletion takes place from another end. The end at which the insertion occurs is known as the rear end whereas the end at which the deletion occurs is known as front end.
Deque is a linear data structure in which the insertion and deletion operations are performed from both ends. We can say that deque is a generalized version of the queue.
Let's look at some properties of deque.
In deque, the insertion and deletion operation can be performed from one side. The stack follows the LIFO rule in which both the insertion and deletion can be performed only from one end; therefore, we conclude that deque can be considered as a stack.
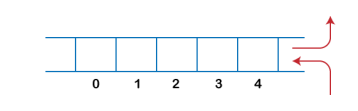
In deque, the insertion can be performed on one end, and the deletion can be done on another end. The queue follows the FIFO rule in which the element is inserted on one end and deleted from another end. Therefore, we conclude that the deque can also be considered as the queue.
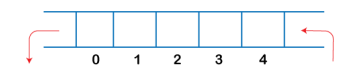
There are two types of Queues, Input-restricted queue, and output-restricted queue.
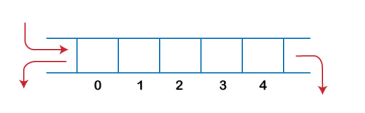
2. Output-restricted queue: The output-restricted queue means that some restrictions are applied to the deletion operation. In an output-restricted queue, the deletion can be applied only from one end, whereas the insertion is possible from both ends.
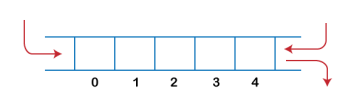
Operations on Deque
The following are the operations applied on deque:
Other than insertion and deletion, we can also perform peek operation in deque. Through peek operation, we can get the front and the rear element of the dequeue.
We can perform two more operations on dequeue:
Memory Representation
The deque can be implemented using two data structures, i.e., circular array, and doubly linked list. To implement the deque using circular array, we first should know what is circular array.
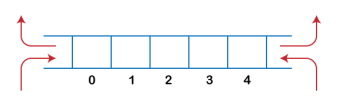
What is a circular array?
An array is said to be circular if the last element of the array is connected to the first element of the array. Suppose the size of the array is 4, and the array is full but the first location of the array is empty. If we want to insert the array element, it will not show any overflow condition as the last element is connected to the first element. The value which we want to insert will be added in the first location of the array.
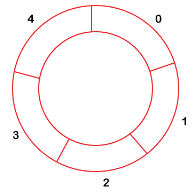
Applications of Deque
Implementation of Deque using a circular array
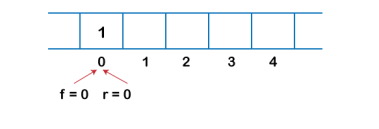
The following are the steps to perform the operations on the Deque:
Enqueue operation
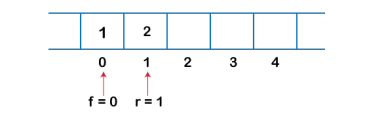
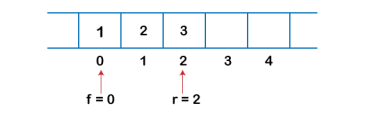
4. Suppose we are again inserting the element from the rear end. To insert the element, we will first increment the rear, and now rear points to the third element.
5. If we want to insert the element from the front end, and insert an element from the front, we have to decrement the value of front by 1. If we decrement the front by 1, then the front points to -1 location, which is not any valid location in an array. So, we set the front as (n -1), which is equal to 4 as n is 5. Once the front is set, we will insert the value as shown in the below figure:
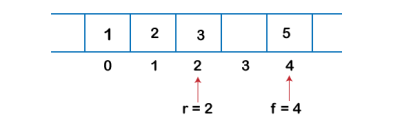
Dequeue Operation
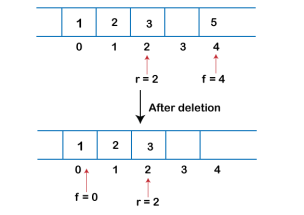
2. If we want to delete the element from rear end then we need to decrement the rear value by 1, i.e., rear=rear-1 as shown in the below figure:
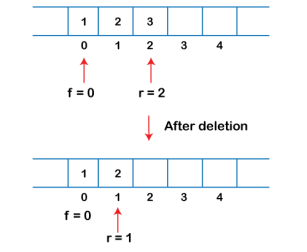
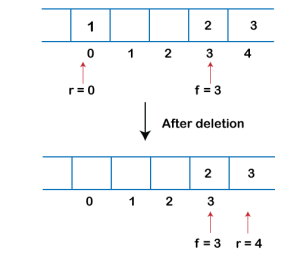
3. If the rear is pointing to the first element, and we want to delete the element from the rear end then we have to set rear=n-1 where n is the size of the array as shown in the below figure:
Let's create a program of deque.
The following are the six functions that we have used in the below program:
Output:
TEXT BOOKS:
REFERENCE BOOKS: