Unit-3

Relations & Functions

Q1) Define relation.

A1)

Let A and B are two sets then a relation or binary relation from A to B is a subset of A×B.

Suppose R is a relation from A to B. then R is a set of ordered pairs where each first element comes from A and each second element comes from B

For each pair a ∈ A and b ∈ B, exactly one of the following is true-

(I). (a, b) ∈ R, we then say “ a is R-related to B” can be written as- aRb

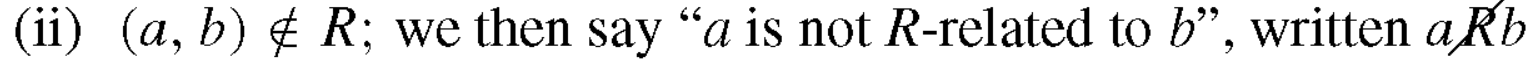
Domain and range of a relation-

The domain of a relation R is the set of all first elements of the ordered pairs which belongs to R, and range is the set of second elements.

Q2) Define inverse relation with an example.

A2)

Inverse relation-

Let R be a relation from a set A to a set B. then the inverse of this relation is the relation from B to A which consists of those ordered pairs which, when reversed, belong to R that is-

Example: Let A = {10, 11, 12} and B = {a, b, c} then inverse of

R = {(10, a), (10, c), (12, b)} is 

Q3) What are the properties of relations?

A3)

Reflexive relation-

Definition-

Let R be a relation defined in a set A; then R is reflexive if aRaholds for all a ∈A , i.e., if (a, a) ∈R for all a ∈A

Example- Let A = {x, y, z} and R = {(x, x), (y, y), (z, z)} then R is a reflexive relation in A.

Symmetric relation-

Definition-

A relation R defined in set A is said to be ‘symmetric’ if bRa holds whenever aRb holds for b ∈A , i.e., R is symmetric in A if(a, b) ∈R ⇒(b, a) ∈R

Transitive relation-

Definition-

A relation R in set A is said to be transitive if (a, b) ∈R (b, c) ∈R ⇒(a, c) ∈R

Example 2: Let A = {1, 2, 3} and R = {(1, 1), (2, 2), (2, 3), (3, 2), (3, 3)} then R is transitive

Equivalence relation-

Definition-

A relation R in a set A is said to be an equivalence relation in A, if R is reflexive,symmetric and transitive.

Example- Let A = {a, b, c}, and R = {(a, a), (a, b), (b, a), (b, b), (b, c), (c, a), (c, b), (c, c)} then R is an equivalence relation in A.

Anti-symmetric relation-

Definition-

Let R be a relation in a set A, then R is called anti-symmetric.

(a, b) ∈R, (b, a) ∈R ⇒a = b ∀a, b ∈R

Q4) A = {2, 3}, B = {3, 4, 5, 6} and R is a relation from A to B defined as follows:

(a, b) ∈R if “a divides b” write the solution set of R.

A4)

 2 divides 4 and 2 divides 6

⇒(2, 4) ∈R and (2, 6) ∈R

3 divides 3, 3 divides 6

⇒(3, 3) ∈R and (3, 6) ∈R

4 divides 4 ⇒(4, 4) ∈R

Thus R = {(2, 4), (2, 6), (3, 3), (3, 6), (4, 4)}

Q5) Let Z denote the set of integers and the relation R in Z be defined by “aRb” if f a – b is an even integer”. Then show that R is an equivalence relation.

A5)

1. R is reflexive; since

∅ = a −a is even, hence aRa for every a∈Z.

2. R is symmetric:

If a – b is even then b – a = – (a – b) is also even hence aRb⇒bRa

3. R is transitive: for if aRb and bRc then both a – b and b – c are even.

Consequently, a – c = (a – b) + (b – c) is also even.

∴aRb and bRc⇒aR c

Thus, R is an equivalence relation.

Q6) Let A = {1, 2, 3, 4} and R, S be two relations on A defined by

R = {(1, 2), (1, 3), (2, 4), (3, 2)};

S = {(1, 4), (4, 3), (2, 3), (3, 1)} find SoR.

A6)

(1, 2) ∈R and (2, 3) ∈S ⇒(1, 3) ∈S o R

(1, 3) ∈R and (3, 1) ∈S ⇒(1, 3) ∈S o R

(3, 2) ∈R and (2, 3) ∈S ⇒(3, 3) ∈S o R

(2, 4) ∈R and (4, 3) ∈S ⇒(2, 3) ∈S o R

Thus S oR= {(1, 3), (1, 1), (3, 3), (2, 3)}

Q7) Let A = {1, 2, 3} and R = {(1, 2), (1, 3), (2, 3)}, then find

A7)

The matrix can be represented as below-

Or in matrix form-

Q8) Let A = {1, 4, 5} and R = {(1, 4), (1, 5), (4, 1), (4, 4), (5, 5)} then find

A8)

It is given that-

R = {(1, 4), (1, 5), (4, 1), (4, 4), (5, 5)}

Then the relation matrix will be-

Q9) Let A = {1, 2, 3, 4} and R = {(1, 1), (1, 2), (2, 1), (2, 2), (2, 3), (2, 4), (3, 4), (4, 1), (4, 4)}

Represent the relation by graph.

A9)

The diagraph of R can be made as-

Q10) Find the number of ways to partition of 10 peoples into four groups

So that two teams contain 3 persons and two teams contain 2 persons.

A10)

By using above theorem, we get-

ordered partitions

Here the group form an unordered partition so that we divide m’ by Because of the two cells with three elements each and Because of the two cells with two elements each.

 So that-

Q11) Draw the Hasse diagram of positive division of 36.

A11)

We have

Suppose R is the partial order relation on

The Hasse diagram will be-

Q12) Show that the inverse of an invertible mapping is unique.

A12)

Let

By any invertible mapping,

Let,

g: Y→X

h: Y→X

are two different inverse mapping of f.

Let y ∈ Y and

Now-

And

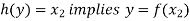
so that-

and

Now-

Which shows that g(y) = h(y)∀ y ∈ Y

So that the inverse of f is unique.

Q13) Prove that is both one-one and onto then is both one-one and onto.

A13)

Let f: X→Ybe both one-one and onto.

Then there exist elements ∈X, and elements∈Y

Such that

f() = , and f () =

Or

= () and = ()

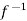Now,

Let (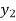) = (), then

() = ()

⇒ =

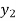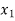⇒f(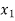) = f ()

⇒ =

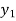Thus is one-one

Since f is onto, for y∈Y, there is some element x∈X, such that f (x) = y.

Now

f(x) = y

⇒x=

So that is onto.

Hence 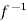is both one-one and onto.

Q14) Define function.

A14)

Let A and B be any two sets. A relation f from A to B is called function if for every

a∈A there is a unique element b ∈B , such that (a, b) ∈f.

If f is a function from A to B, then f is a function from A to B such that-

1. Domain f = A

2. Whenever (a, b)∈ f and (a, c)∈ f then b = c

We can denote the function as-

f: A →B, means f is a function from A to B.

Given any function f: A →B, then f(a) = b means (a, b) ∈ f

Here element ‘a’ which belongs to A is called an argument of the function f and f(a) is called the value of the function for the argument a.