UNIT–4
Algebraic systems
Binary operations-
A binary operation * is a set A is a function from A × A to A.
If * is a binary operation in a set A then than for the * image of the ordered pair (a, b) ∈ A×A, we write a*b.
For example:
Addition + is a binary operation in the set of natural number N, integer Z and real number R.
Multiplication is a binary operation in N, Q, Z, R and C.
General properties-
Propery-1: Let A be any set. A binary operation * A × A →A is said to be commutative if for every a, a, b ∈A.
a* b = b * a
Property-2:Let A be a non-empty set. A binary operation *; A × A →A is said to be associative if
a* b) * c = a * (b * c) for every a, b, c ∈A.
Property-3: Let * be a binary operation on a non-empty set A. If there exists an element e ∈A such that e * a = a * e = a for every a ∈A, then the element e is called identity with respect to * in A.
Property-4: Let * be a binary operation on a non-empty set A and e be the identity element in A with respect the operation *. An element a ∈A is said to be invertible if there exists an element b ∈A such that
a* b = b * a = e
In which case a andb are inverses of each other. For the operation * if b is the inverses of a ∈A then we can write b = 
Cancellation laws-
A binary operation denoted by * in a set A, is said to satisfy.
(i) Left cancellation law if for all a, b, c ∈A,
a* b = a * c ⇒b = c
(ii) Right cancellation law if for all a, b, c ∈A
b* a = c * a ⇒b = c
Algebraic system-
If A is a set and * is a binary operation on A, then (A, *) is called an algebraic structure.
Example: Let R be the set of real numbers, then (R, +) is an algebraic structure.
Example: If N denotes the set of natural numbers then (N, +) is an algebraic structure.
Semi-group-
Let S be a non-empty set and * be a binary operation on S. The algebraic (S, *) is called a semi-group if the operation * is associative. In other words, the groupoid is a semi-group if
(a* b) * c = a * (b * c) for all a, b, c ∈S
Thus, a semi-group requires the following:
(i) A sets.
(ii) A binary operation * defined on the elements of S.
(iii) Closure, a * b whenever a, b ∈S.
(iv) Associativity i(a * b) * c = a * (b * c) for all a, b, c ∈S.
Example: Let N be the set of natural numbers. Then (N, +) and (N, *) are semi-groups.
Homomorphism of semi-groups-
Let (S, *) and (T, 0) be any two semi-groups. A mapping f: S →T such that for any two elements a, b ∈S
f(a * b) = f (a) o f(b) is called a semi-group homomorphism.
Isomorphism of semi-groups-
Let (S, *) and (T, 0) be any two semi-groups. A homomorphism f: S →T is called a semi-group isomorphism if f is one-to-one and onto.
If f: S →T is an isomorphism then (S, *) and (T, 0) are said to be isomorphic.
Monoid-
A semi-group (M, *) with an identity element with respect to the binary operation * is called a monoid. In other words, an algebraic system (M, *) is called a monoid if:
(i) (a * b) * c = a * (b * c) ∀a, b, c ∈M.
(ii) There exists an element e ∈M such that e * a = a * e = a ∀a ∈M.
Example: Let Z be the set of integers (Z, +) is a monoid 0 is the identity element in Z with respect
to +.
Cyclic monoid-
A monoid (M, *) is said to be cyclic if there exists an element a ∈M. Such that every element of M can be expressed as some power of a. If M is a cyclic monoid such that every element is some power of
a∈M, then a is called the generator of M. A cyclic monoid is commutative and a cyclic monoid is commutative and a cyclic monoid may have more than one generator.
Monoid homomorphism-
Let (M, *) and (T, 0) be any two monoidsemand et denote the identity elements of
(M, *) and (T, 0) respectively. A mapping
f: M →T such that for any two elements a, b ∈M
f(a * b) = f (a) o f(b)
and
Is called a monoid homomorphism.
A group is an algebraic structure (G, *) in which the binary operation * on G satisfiesthe following conditions:
Condition-1: for all a, b, c, ∈G
a* (b * c) = (a * b) * c (associativity)
Condition-2:there exists an elements e ∈G such that for any a ∈G
a* e= e * a = a (existence of identity)
Condition-3: for every a ∈G, there exists an element denoted by 
in G such that
a* 
= 
* a = e
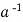is called the inverse of a in G.
Example: (Z, +) is a groupwhere Z denote the set of integers.
Example: (R, +) is a group where R denote the set of real numbers.
Abelian group-
Let (G, *) be a group. If * is commutative that is
a* b = b * a for all a, b ∈G then (G, *) is called an Abelian group.
Finite group-
A group G is said to be a finite group if the set G is a finite set.
Infinite group-
A group G, which is not finite is called an infinite group.
Order of a finite group-
The order of a finite group (G, *) is the number of distinct element in G. The order of
G is denoted by O (G) or by |G|.
Example: If G = {1, -1, i, -i} where i= 
, then show that G is an abelian group with respect to multiplication as a binary operation.
Sol.
First we will construct a composition table-
. | 1 | -1 | i | -i |
1 | 1 | -1 | i | -i |
-1 | -1 | 1 | -i | i |
i | i | -i | -1 | 1 |
-i | -i | i | 1 | -1 |
It is clear from the above table that algebraic structure (G, .) is closed and satisfies the following conditions.
Associativity- For any three elements a, b, c ∈G (a ⋅b) ⋅c = a ⋅(b ⋅c)
Since
1 ⋅(−1 ⋅i) = 1 ⋅−i= −i
(1 ⋅−1) ⋅i= −1 ⋅i= −i
⇒1 ⋅(−1 ⋅i) = (1 ⋅−1) i
Similarly with any other three elements of G the properties holds.
∴Associative law holds in (G, ⋅)
Existence of identity: 1 is the identity element (G, ⋅) such that 1 ⋅a = a = a ⋅1 ∀a ∈G
Existence of inverse: 1 ⋅1 = 1 = 1 ⋅1 ⇒1 is inverse of 1
(−1) ⋅(−1) = 1 = (−1) ⋅(−1) ⇒–1 is the inverse of (–1)
i⋅(−i) = 1 = −i⋅i⇒–iis the inverse of iin G.
−i⋅i= 1 = i⋅(−i) ⇒iis the inverse of –iin G.
Hence inverse of every element in G exists.
Thus all the axioms of a group are satisfied.
Commutativity: a ⋅b = b ⋅a ∀a, b ∈G hold in G
1 ⋅1 = 1 = 1 ⋅1, −1 ⋅1 = −1 = 1 ⋅−1
i⋅1 = i= 1 ⋅i; i⋅−i= −i⋅i= 1 = 1 etc.
Commutative law is satisfied
Hence (G, ⋅) is an abelian group.
Example-
Prove that the set Z of all integers with binary operation * defined by a * b = a + b + 1 ∀a, b ∈G is an abelian group.
Sol: Sum of two integers is again an integer; therefore a +b ∈Z ∀a, b ∈Z
⇒a +b + 1 ⋅∈Z ∀a, b ∈Z
⇒Z is called with respect to *
Associative law for all a, b, a, b ∈G we have (a * b) * c = a * (b * c) as
(a* b) * c = (a + b + 1) * c
= a + b + 1 + c + 1
= a + b + c + 2
Also
a* (b * c) = a * (b + c + 1)
= a + b + c + 1 + 1
= a + b + c + 2
Hence (a * b) * c = a * (b * c) ∈a, b ∈Z.
Let (G, *) be a group and H, be a non-empty subset of G. If (H, *) is itself is a group,then (H, *) is called sub-group of (G, *).
Example-Let a = {1, –1, i, –i} and H = {1, –1}
G and H are groups with respect to the binary operation, multiplication.
H is a subset of G, therefore (H, X) is a sub-group (G, X).
Theorem-
If (G, *) is a group and H ≤G, then (H, *) is a sub-group of (G, *) if and only if
(i) a, b ∈H ⇒a * b ∈H;
(ii) a∈H ⇒
∈H
Proof:
If (H, *) is a sub-group of (G, *), then both the conditions are obviously satisfied.
We, therefore prove now that if conditions (i) and (ii) are satisfied then (H, *) is a sub-group of (G, *).
To prove that (H, *) is a sub-group of (G, *) all that we are required to prove is : * is associative in
H and identity e ∈H.
That * is associative in H follows from the fact that * is associative in G.
Also,
a∈H ⇒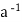
∈H by (ii) and e ∈H and 
∈H ⇒a * 
= e ∈H by (i)
Hence, H is a sub-group of G.
Cosets-
Let (H, *) be a sub-group (G, *) and a ∈G
Then the sub-set:
a* H = {a * h: h ∈H}is called a left coset of H in G, and the subset
H * G = {h * a: h ∈H}is called a right coset of H in G.
Theorem: If (H, *) is a sub-group (G, *), then a * H = H if and only if a ∈H.
Proof: Let a * H = H
Since e ∈H then a = a * e ∈a * H
Hence a ∈H
Conversely
Let a ∈H then a * H ⊆H
(H, *) is a sub-group.
∴a∈H, h ∈H ⇒
* h ∈H.
Now h ∈H
⇒h = a * (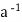
* h) ∈a * H
∴h∈H ⇒h ∈a * H
⇒H ⊆a * H
Hence a * H = H
Homomorphism-
Let (G, *) and (
, 
) be any two groups. A mapping f: G →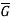
is called ahomomorphism of G to 
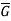if.
f(a * b) = f (a) 
f (b) ∀a, b ∈G
Example: Let G = R, the set of real numbers and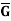 
= R – {u)
(G, +) and (
, ⋅) are groups. Define a mapping f: G →G by
f(a) = 
∀a ∈G
Clearly f (a + b) = 
= 
= f (a) ⋅f (b)
⇒fis a homomorphism of G into G.
Kernel of homomorphism-
Let G and G be any two groups and f: G →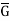
be a homomorphism. Then Kernel of f denoted by Ker f the set K = (a ∈G: f (a) = 
).
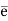Where e is the identity of 
.
Example: Let G be (Z, +) i.e., the group of integers under addition and let f: G →G defined by
∅(x) = 3x ∀x ∈G. Prove that f is homomorphism, determine its Kernel.
Solution: We have ∅(x) = 3x ∀x ∈G
∀x, y ∈G ⇒x + y ∈G (∴G is a group under addition)
Now
f(x + y) = 3 (x + y)
= 3x + 3y
= f (x) + f (y)
Hence f is homomorphism.
Kernel of homomorphism consists of half of zero i.e., the integers whose double is zero.
Thus K = {0}
