UNIT- 2
Searching and Sorting Techniques
Searching
Searching is the process of finding some particular element in the list. If the element is present in the list, then the process is called successful and the process returns the location of that element, otherwise the search is called unsuccessful.
There are two popular search methods that are widely used in order to search some item into the list. However, choice of the algorithm depends upon the arrangement of the list.
Linear Search
Linear search is the simplest search algorithm and often called sequential search. In this type of searching, we simply traverse the list completely and match each element of the list with the item whose location is to be found. If the match found then location of the item is returned otherwise the algorithm return NULL.
Linear search is mostly used to search an unordered list in which the items are not sorted. The algorithm of linear search is given as follows.
Algorithm
SET POS = I
PRINT POS
Go to Step 6
[END OF IF]
SET I = I + 1
[END OF LOOP]
PRINT " VALUE IS NOT PRESENTIN THE ARRAY "
[END OF IF]
Complexity of algorithm
Complexity | Best Case | Average Case | Worst Case |
Time | O(1) | O(n) | O(n) |
Space |
|
| O(1) |
C Program
Output:
Enter Item which is to be searched
20
Item not found
Enter Item which is to be searched
23
Item found at location 2
Java Program
Output:
Enter Item ?
23
Item found at location 2
Enter Item ?
22
Item not found
C# Program
Output:
Enter the item value
78
Item Found at Location 10
Enter the item value
22
Item not found
Python Program
Output:
Enter the item which you want to search 2
Item found at location 2
Enter the item which you want to search 101
Item not found
Binary Search
Binary search is the search technique which works efficiently on the sorted lists. Hence, in order to search an element into some list by using binary search technique, we must ensure that the list is sorted.
Binary search follows divide and conquer approach in which, the list is divided into two halves and the item is compared with the middle element of the list. If the match is found then, the location of middle element is returned otherwise, we search into either of the halves depending upon the result produced through the match.
Binary search algorithm is given below.
BINARY_SEARCH(A, lower_bound, upper_bound, VAL)
END = upper_bound, POS = - 1
SET POS = MID
PRINT POS
Go to Step 6
ELSE IF A[MID] > VAL
SET END = MID - 1
ELSE
SET BEG = MID + 1
[END OF IF]
[END OF LOOP]
PRINT "VALUE IS NOT PRESENT IN THE ARRAY"
[END OF IF]
Complexity
SN | Performance | Complexity |
1 | Worst case | O(log n) |
2 | Best case | O(1) |
3 | Average Case | O(log n) |
4 | Worst case space complexity | O(1) |
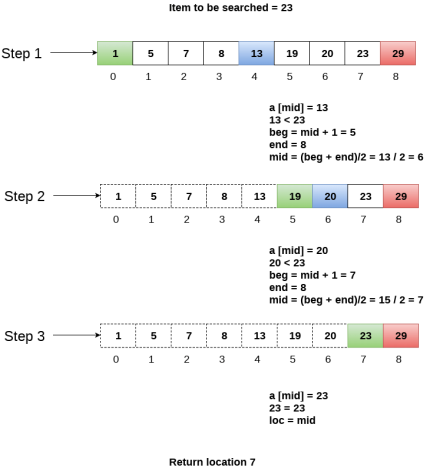
Example
Let us consider an array arr = {1, 5, 7, 8, 13, 19, 20, 23, 29}. Find the location of the item 23 in the array.
In 1ststep :
in Second step:
in third step:
Binary Search Program using Recursion
C program
Output:
Enter the item which you want to search
19
Item found at location 2
Java
Output:
Enter the item which you want to search
45
the location of the item is 5
C#
Output:
Enter the item which you want to search
20
Item found at location 3
Python
Output:
Enter the item which you want to search ?
96
Item found at location 9
Enter the item which you want to search ?
101
Item not found
Binary Search function using Iteration
Hashing
In data structures,
Advantage-
Unlike other searching techniques,
Hashing Mechanism-
In hashing,
Hash Key Value-
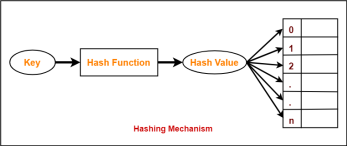
Hash Function-
Hash function is a function that maps any big number or string to a small integer value. |
Hash function takes the data item as an input and returns a small integer value as an output.
The small integer value is called as a hash value.
Hash value of the data item is then used as an index for storing it into the hash table.
Types of Hash Functions-
There are various types of hash functions available such as-
It depends on the user which hash function he wants to use.
Properties of Hash Function-
The properties of a good hash function are-
Collision in Hashing-
In hashing,
When the hash value of a key maps to an already occupied bucket of the hash table, it is called as a Collision. |
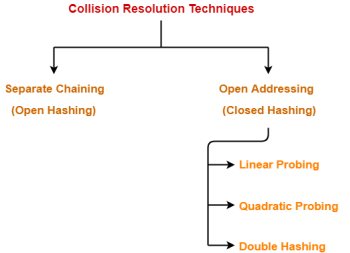
Collision Resolution Techniques-
Collision Resolution Techniques are the techniques used for resolving or handling the collision. |
Collision resolution techniques are classified as-
Separate Chaining-
To handle the collision,
Time Complexity-
For Searching-
For Deletion-
Load Factor (α)-
Load factor (α) is defined as-

If Load factor (α) = constant, then time complexity of Insert, Search, Delete = Θ(1)
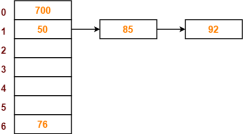
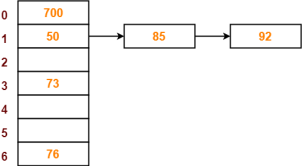
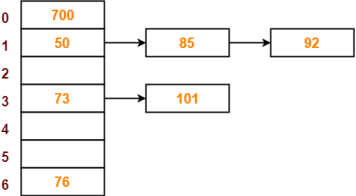
PRACTICE PROBLEM BASED ON SEPARATE CHAINING-
Problem-
Using the hash function ‘key mod 7’, insert the following sequence of keys in the hash table-
50, 700, 76, 85, 92, 73 and 101
Use separate chaining technique for collision resolution.
Solution-
The given sequence of keys will be inserted in the hash table as-
Step-01:

Step-02:

Step-03:

Step-04:

Step-05:
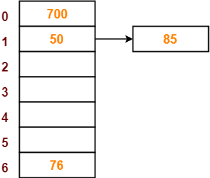
Step-06:
Step-07:
Step-08:
Bubble Sort
In Bubble sort, each element of the array is compared with its adjacent element. The algorithm processes the list in passes. A list with n elements requires n-1 passes for sorting. Consider an array A of n elements whose elements are to be sorted by using Bubble sort. The algorithm processes like following.
Algorithm:
SWAP A[J] and A[i]
[END OF INNER LOOP]
[END OF OUTER LOOP
Complexity
Scenario | Complexity |
Space | O(1) |
Worst case running time | O(n2) |
Average case running time | O(n) |
Best case running time | O(n2) |
C Program
Output:
Printing Sorted Element List . . .
7
9
10
12
23
34
34
44
78
101
C++ Program
Output:
Printing Sorted Element List ...
7
9
10
12
23
23
34
44
78
101
Java Program
Output:
Printing Sorted List . . .
7
9
10
12
23
34
34
44
78
101
C# Program
Output:
Printing Sorted Element List . . .
7
9
10
12
23
34
34
44
78
101
Python Program
Output:
Printing Sorted Element List . . .
7
9
10
12
23
34
34
44
78
101
Rust Program
Output:
Printing Sorted Element List . . .
7
9
10
12
23
34
34
44
78
101
4
JavaScript Program
Output:
Printing Sorted Element List ...
7
9
10
12
23
23
34
44
78
101
PHP Program
Output:
Printing Sorted Element List ...
7
9
10
12
23
23
34
44
78
101
Selection Sort
In selection sort, the smallest value among the unsorted elements of the array is selected in every pass and inserted to its appropriate position into the array.
First, find the smallest element of the array and place it on the first position. Then, find the second smallest element of the array and place it on the second position. The process continues until we get the sorted array.
The array with n elements is sorted by using n-1 pass of selection sort algorithm.
Therefore, by following the above explained process, the elements A[0], A[1], A[2],...., A[n-1] are sorted.
Example
Consider the following array with 6 elements. Sort the elements of the array by using selection sort.
A = {10, 2, 3, 90, 43, 56}.
Pass | Pos | A[0] | A[1] | A[2] | A[3] | A[4] | A[5] |
1 | 1 | 2 | 10 | 3 | 90 | 43 | 56 |
2 | 2 | 2 | 3 | 10 | 90 | 43 | 56 |
3 | 2 | 2 | 3 | 10 | 90 | 43 | 56 |
4 | 4 | 2 | 3 | 10 | 43 | 90 | 56 |
5 | 5 | 2 | 3 | 10 | 43 | 56 | 90 |
Sorted A = {2, 3, 10, 43, 56, 90}
Complexity
Complexity | Best Case | Average Case | Worst Case |
Time | Ω(n) | θ(n2) | o(n2) |
Space |
|
| o(1) |
Algorithm
SELECTION SORT(ARR, N)
[END OF LOOP]
SMALLEST (ARR, K, N, POS)
IF SMALL > ARR[J]
SET SMALL = ARR[J]
SET POS = J
[END OF IF]
[END OF LOOP]
C Program
Output:
printing sorted elements...
7
9
10
12
23
23
34
44
78
101
C++ Program
Output:
printing sorted elements...
7
9
10
12
23
23
34
44
78
101
Java Program
Output:
printing sorted elements...
7
9
10
12
23
23
34
44
78
101
C# Program
Output:
printing sorted elements...
7
9
10
12
23
23
34
44
78
101
Python Program
Output:
printing sorted elements...
7
9
10
12
23
23
34
44
78
101
Rust Program
Output:
printing sorted elements...
7
9
10
12
23
23
34
44
78
101
JavaScript Program
Output:
printing sorted elements ...
7
9
10
12
23
23
34
44
78
101
PHP Program
Output:
printing sorted elements ...
7
9
10
12
23
23
34
44
78
101
Insertion Sort
Insertion sort is the simple sorting algorithm which is commonly used in the daily lives while ordering a deck of cards. In this algorithm, we insert each element onto its proper place in the sorted array. This is less efficient than the other sort algorithms like quick sort, merge sort, etc.
Technique
Consider an array A whose elements are to be sorted. Initially, A[0] is the only element on the sorted set. In pass 1, A[1] is placed at its proper index in the array.
In pass 2, A[2] is placed at its proper index in the array. Likewise, in pass n-1, A[n-1] is placed at its proper index into the array.
To insert an element A[k] to its proper index, we must compare it with all other elements i.e. A[k-1], A[k-2], and so on until we find an element A[j] such that, A[j]<=A[k].
All the elements from A[k-1] to A[j] need to be shifted and A[k] will be moved to A[j+1].
Complexity
Complexity | Best Case | Average Case | Worst Case |
Time | Ω(n) | θ(n2) | o(n2) |
Space |
|
| o(1) |
Algorithm
SET ARR[J + 1] = ARR[J]
SET J = J - 1
[END OF INNER LOOP]
[END OF LOOP]
C Program
Output:
Printing Sorted Elements . . .
7
9
10
12
23
23
34
44
78
101
C++ Program
Output:
printing sorted elements...
7
9
10
12
23
23
34
44
78
101
Java Program
Output:
Printing sorted elements . . .
7
9
10
12
23
23
34
44
78
101
C# Program
Output:
printing sorted elements . . .
7
9
10
12
23
23
34
44
78
101
Python Program
Output:
printing sorted elements . . .
7
9
10
12
23
23
34
44
78
101
Swift Program
Output:
printing sorted elements...
7
9
10
12
23
23
34
44
78
101
JavaScript Program
Output:
printing sorted elements ...
7
9
10
12
23
23
34
44
78
101
PHP Program
Output:
printing sorted elements ...
7
9
10
12
23
23
34
44
78
101
Merge sort
Merge sort is the algorithm which follows divide and conquer approach. Consider an array A of n number of elements. The algorithm processes the elements in 3 steps.
The main idea behind merge sort is that, the short list takes less time to be sorted.
Complexity
Complexity | Best case | Average Case | Worst Case |
Time Complexity | O(n log n) | O(n log n) | O(n log n) |
Space Complexity |
|
| O(n) |
Example :
Consider the following array of 7 elements. Sort the array by using merge sort.
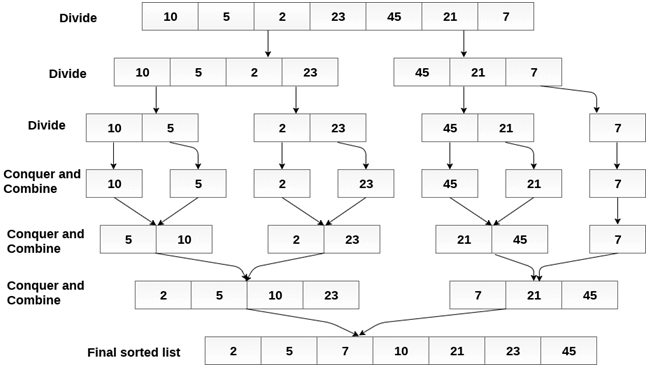
Algorithm
IF ARR[I] < ARR[J]
SET TEMP[INDEX] = ARR[I]
SET I = I + 1
ELSE
SET TEMP[INDEX] = ARR[J]
SET J = J + 1
[END OF IF]
SET INDEX = INDEX + 1
[END OF LOOP]
Step 3: [Copy the remaining
elements of right sub-array, if
any]
IF I > MID
Repeat while J <= END
SET TEMP[INDEX] = ARR[J]
SET INDEX = INDEX + 1, SET J = J + 1
[END OF LOOP]
[Copy the remaining elements of
left sub-array, if any]
ELSE
Repeat while I <= MID
SET TEMP[INDEX] = ARR[I]
SET INDEX = INDEX + 1, SET I = I + 1
[END OF LOOP]
[END OF IF]
SET ARR[K] = TEMP[K]
SET K = K + 1
[END OF LOOP]
MERGE_SORT(ARR, BEG, END)
SET MID = (BEG + END)/2
CALL MERGE_SORT (ARR, BEG, MID)
CALL MERGE_SORT (ARR, MID + 1, END)
MERGE (ARR, BEG, MID, END)
[END OF IF]
C Program
Output:
printing the sorted elements
7
9
10
12
23
23
34
44
78
101
Java Program
Output:
Sorted array
23
23
23
34
45
65
67
89
90
101
C# Program
Output:
Sorted array
23
23
23
34
45
65
67
89
90
101
Quick Sort
Quick sort is the widely used sorting algorithm that makes n log n comparisons in average case for sorting of an array of n elements. This algorithm follows divide and conquer approach. The algorithm processes the array in the following way.
Ensure that, a[loc] is less than a[right].
- if this is the case, then continue with the comparison until loc becomes equal to left.
- [loc] <a[right], then swap the two values and go to step 2.
- Set, loc = left.
Complexity
Complexity | Best Case | Average Case | Worst Case |
Time Complexity | O(n) for 3 way partition or O(n log n) simple partition | O(n log n) | O(n2) |
Space Complexity |
|
| O(log n) |
Algorithm
PARTITION (ARR, BEG, END, LOC)
AND LOC != RIGHT
SET RIGHT = RIGHT - 1
[END OF LOOP]
SET FLAG = 1
ELSE IF ARR[LOC] > ARR[RIGHT]
SWAP ARR[LOC] with ARR[RIGHT]
SET LOC = RIGHT
[END OF IF]
Repeat while ARR[LOC] >= ARR[LEFT] AND LOC != LEFT
SET LEFT = LEFT + 1
[END OF LOOP]
SET FLAG = 1
ELSE IF ARR[LOC] < ARR[LEFT]
SWAP ARR[LOC] with ARR[LEFT]
SET LOC = LEFT
[END OF IF]
[END OF IF]
QUICK_SORT (ARR, BEG, END)
CALL PARTITION (ARR, BEG, END, LOC)
CALL QUICKSORT(ARR, BEG, LOC - 1)
CALL QUICKSORT(ARR, LOC + 1, END)
[END OF IF]
C Program
Output:
The sorted array is:
23
23
23
34
45
65
67
89
90
101
Java Program
Output:
The sorted array is:
23
23
23
34
45
65
67
89
90
101
C# Program
Output:
The sorted array is:
23
23
23
34
45
65
67
89
90
101
Radix Sort
Radix sort processes the elements the same way in which the names of the students are sorted according to their alphabetical order. There are 26 radix in that case due to the fact that, there are 26 alphabets in English. In the first pass, the names are grouped according to the ascending order of the first letter of names.
In the second pass, the names are grouped according to the ascending order of the second letter. The same process continues until we find the sorted list of names. The bucket are used to store the names produced in each pass. The number of passes depends upon the length of the name with the maximum letter.
In the case of integers, radix sort sorts the numbers according to their digits. The comparisons are made among the digits of the number from LSB to MSB. The number of passes depend upon the length of the number with the most number of digits.
Complexity
Complexity | Best Case | Average Case | Worst Case |
Time Complexity | Ω(n+k) | θ(nk) | O(nk) |
Space Complexity |
|
| O(n+k) |
Example
Consider the array of length 6 given below. Sort the array by using Radix sort.
A = {10, 2, 901, 803, 1024}
Pass 1: (Sort the list according to the digits at 0's place)
10, 901, 2, 803, 1024.
Pass 2: (Sort the list according to the digits at 10's place)
02, 10, 901, 803, 1024
Pass 3: (Sort the list according to the digits at 100's place)
02, 10, 1024, 803, 901.
Pass 4: (Sort the list according to the digits at 1000's place)
02, 10, 803, 901, 1024
Therefore, the list generated in the step 4 is the sorted list, arranged from radix sort.
Algorithm
in LARGE
numbered DIGIT
[END OF LOOP]
[END OF LOOP]
C Program
Output:
The sorted array is:
23
23
23
34
45
65
67
89
90
101
Java Program
Output:
The sorted array is:
23
23
23
34
45
65
67
89
90
101
C# Program
Output:
The sorted array is:
23
23
23
34
45
65
67
89
90
101
Algorithm Analysis
Analysis of efficiency of an algorithm can be performed at two different stages, before implementation and after implementation, as
A priori analysis −This is defined as theoretical analysis of an algorithm. Efficiency of algorithm is measured by assuming that all other factors e.g. speed of processor, are constant and have no effect on implementation.
A posterior analysis −This is defined as empirical analysis of an algorithm. The chosen algorithm is implemented using programming language. Next the chosen algorithm is executed on target computer machine. In this analysis, actual statistics like running time and space needed are collected.
Algorithm analysis is dealt with the execution or running time of various operations involved. Running time of an operation can be defined as number of computer instructions executed per operation.
Algorithm Complexity
Suppose X is treated as an algorithm and N is treated as the size of input data, the time and space implemented by the Algorithm X are the two main factors which determine the efficiency of X.
Time Factor −The time is calculated or measured by counting the number of key operations such as comparisons in sorting algorithm.
Space Factor −The space is calculated or measured by counting the maximum memory space required by the algorithm.
The complexity of an algorithm f(N) provides the running time and / or storage space needed by the algorithm with respect of N as the size of input data.
Space Complexity
Space complexity of an algorithm represents the amount of memory space needed the algorithm in its life cycle.
Space needed by an algorithm is equal to the sum of the following two components
A fixed part that is a space required to store certain data and variables (i.e. simple variables and constants, program size etc.), that are not dependent of the size of the problem.
A variable part is a space required by variables, whose size is totally dependent on the size of the problem. For example, recursion stack space, dynamic memory allocation etc.
Space complexity S(p) of any algorithm p is S(p) = A + Sp(I) Where A is treated as the fixed part and S(I) is treated as the variable part of the algorithm which depends on instance characteristic I. Following is a simple example that tries to explain the concept
Algorithm
SUM(P, Q)
Step 1 - START
Step 2 - R ← P + Q + 10
Step 3 - Stop
Here we have three variables P, Q and R and one constant. Hence S(p) = 1+3. Now space is dependent on data types of given constant types and variables and it will be multiplied accordingly.
Time Complexity
Time Complexity of an algorithm is the representation of the amount of time required by the algorithm to execute to completion. Time requirements can be denoted or defined as a numerical function t(N), where t(N) can be measured as the number of steps, provided each step takes constant time.
For example, in case of addition of two n-bit integers, N steps are taken. Consequently, the total computational time is t(N) = c*n, where c is the time consumed for addition of two bits. Here, we observe that t(N) grows linearly as input size increases.
TEXT BOOKS:
REFERENCE BOOKS: