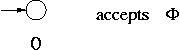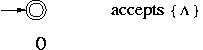ALC
Unit-2Nondeterminism and Kleene’s Theorem
2.1 Nondeterministic finite automataIn NDFA, for a particular input symbol, the machine can move to any combination of the states in the machine. In other words, the exact state to which the machine moves cannot be determined. Hence, it is called Non-Deterministic Automaton. As it has finite number of states, the machine is called Non-Deterministic Finite Machine or Non-Deterministic Finite Automaton. Q → Finite non-empty set of states.
∑ → Finite non-empty set of input symbols.
∂ → Transitional Function.
q0 → Beginning state.
F → Final State
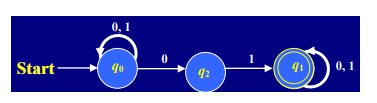
Figure 1 Step 1 For NDFA ExampleA nondeterministic finite automaton (NFA) version of the above DFA --- see Fig. 2.6. ● More intuitive! ● How to design an NFA will be described later?
Figure 2 Step 1 For NDFA Example Some properties of NFA’s (see Fig. 2.6 for the illustration) --- Some transitions may “die,” like ˆ δ (q2, 0). Some transitions have multiple choices, like ˆ δ (q0, 0) = q0 and q2.Example 2.6 --- Design an NFA accepting the following language L = {w | w∈{0, 1}* and ends in 01}.Key takeaway:
∑ → Finite non-empty set of input symbols.
∂ → Transitional Function.
q0 → Beginning state.
F → Final State
● Review of a previous example of DFA
● Original version --- see Fig. (the same as Fig. 1.3.2)
|
|
- In NDFA, for a particular input symbol, the machine can move to any combination of the states in the machine.
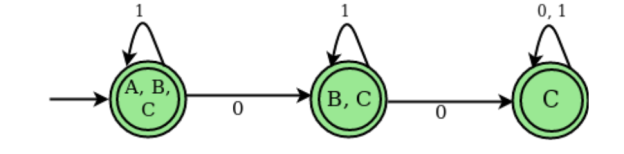
2.2 NFA with null transition Epsilon closure for a given state X is a set of states which can be reached from the states X with only (null) or ε moves including the state X itself.In other words, ε- closure for a state can be obtained by union operation of the ε - closure of the states which can be reached from X with a single ε move in recursive manner.For the above example ∈ closures are as follows: ∈closure(A): {A, B, C}∈closure(B): {B, C}∈closure(C): {C}Deterministic Finite Automata (DFA): DFA is a finite automaton where, for all cases, when a single input is given to a single state, the machine goes to a single state, i.e., all the moves of the machine can be uniquely determined by the present state and the present input symbol.Steps to Convert NFA with ε-move to DFA:Step 1: Take ∈ closure for the beginning state of NFA as beginning state of DFA.Step 2: Find the states that can be traversed from the present for each input symbol (union of transition value and their closures for each state of NFA present in current state of DFA).Step 3: If any new state is found take it as current state and repeat step 2.Step 4: Do repeat Step 2 and Step 3 until no new state present in DFA transition table.Step 5: Mark the states of DFA which contains final state of NFA as final states of DFA. Transition state table for DFA corresponding to above NFA
Fig 3: DFA State diagramKey takeaway:- Epsilon closure for a given state X is a set of states which can be reached from the states X with only (null) or ε moves including the state X itself.
States | 0 | 1 |
A, B, C | B, C | A, B, C |
B, C | C | B, C |
C | C | C |
|
2.3 Equivalence of FA’sIt would seem superficially that deterministic and non-deterministic finite state automata are totally distinct beasts. However, it turns out that they are equivalent. There is a DFA for every language recognized by an NFA that recognizes that language and vice versa.The NFA to DFA conversion algorithm is relatively simple, even though the resulting DFA is substantially more complicated than the original NFA. I will illustrate this equivalence after the hop and also go through a brief example of converting an NFA to an equivalent DFA. DFA and NFA Theorem proof -Let's formally state the theorem we are proving before continuing:Theorem:Let the language L ⊆ Σ* be recognized by NFA N = (Σ , Q, q0, F, δ) and assume L. A DFA D= (Σ, Q ', q'0, F', δ ') exists that also accepts L. (L(N)= L(D)). We are able to prove by induction that D is equal to N by allowing each state in the DFA D to represent a set of states in the NFA N. Let's define the parameters of D: before we start proofing,● Q’ is equal to the power set of Q, Q’ = 2Q● q’0 = {q0}● F’ is the set of states in Q’ that contain any element of F, F’ = {q ∈ Q’|q ∩ F ≠ Ø}● δ’ is the transition function for D. δ’(q ,a ) = Up∈ q δ(p , a)for q ∈ Q’ and a ∈ ΣIt's worth more explaining, I think δ '. Note that in the set of states Q 'in D, each state is a set of states from Q in N itself. Determine the transition δ (p,a) for each state p in state q in Q 'of D (p is a single state from Q). The union of all δ (q, a) is δ(q,a) .Now we will demonstrate δ’ (q0’, x) =δ’(q0 , x) that for every x i.e L(D) = L (N) Simulation of DFA and NFA Let N = (QN , Σ, δN , qN0 , FN ) be a NFA. The equivalent DFA D1 is obtained from the so-called subset construction (also called “power construction”). We define D = (QD, Σ, δD, qD0 , FD),Where ● The alphabet of D is that of N. ● The states of D are sets of states of N: QD = P(QN )● The initial state qD0 of D is {qN0 }.● The final states of D are those sets that contain the final state of N: FD = {S ∈ P(QN )| S ∩ FN 6= ∅} ● The transition function of D arises from the transition function of N as follows: δD(S, a) = Uq∈S δN (q, a)That is, δD(S, a) is the set of all states of N that are reachable from some state q via a. Proposition. For every NFA N, there is a DFA D such that L(D) = L(N) Key takeaway:
- The NFA to DFA conversion algorithm is relatively simple, even though the resulting DFA is substantially more complicated than the original NFA.
- There is a DFA for every language recognized by an NFA that recognizes that language and vice versa.
2.4 Kleene’s Theorem (Part I & Part II) Kleen’s theorem states that an FA accepts any regular language and, conversely, that any language that an FA accepts is regular.Theorem 1: A finite automatic acknowledges every normal language.Proof: The general induction following the recursive description of regular language would prove this. Common step: The languages 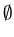 , {
, {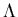 } and {a} for any symbol a in
} and {a} for any symbol a in  are accepted by an FA.
are accepted by an FA.
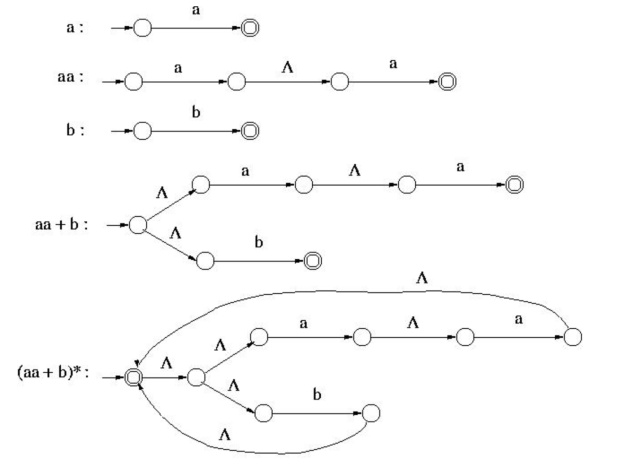
Example:An NFA-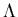 that accepts the language represented by the regular expression is given - (aa + b)* Sol: The given regular expression can be constructed using the operation, as below-
that accepts the language represented by the regular expression is given - (aa + b)* Sol: The given regular expression can be constructed using the operation, as below-
Fig. 4: construction of (aa + b) *
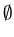 , {
, {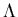 } and {a} for any symbol a in
} and {a} for any symbol a in  are accepted by an FA.
are accepted by an FA.
|
 that accepts the language represented by the regular expression is given - (aa + b)* Sol: The given regular expression can be constructed using the operation, as below-
that accepts the language represented by the regular expression is given - (aa + b)* Sol: The given regular expression can be constructed using the operation, as below-
|
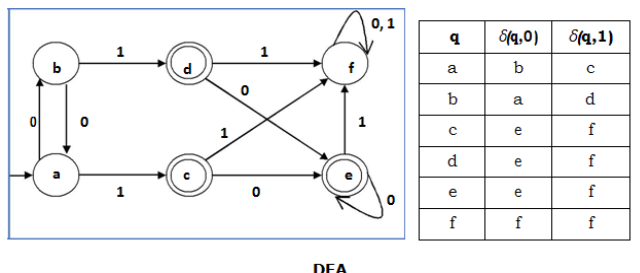
2.5 Minimal Finite Automata If X and Y are two states in a DFA, we can combine these two states into {X, Y} if they are not distinguishable. Two states are distinguishable, if there is at least one string S, such that one of δ (X, S) and δ (Y, S) is accepting and another is not accepting. Hence, a DFA is minimal if and only if all the states are distinguishable. Algorithm Step 1: All the states Q are divided in two partitions: final states and non-final states and are denoted by P0. All the states in a partition are 0th equivalent. Take a counter k and initialize it with 0. Step 2: Increment k by 1. For each partition in Pk, divide the states in Pk into two partitions if they are k-distinguishable. Two states within this partition X and Y are k-distinguishable if there is an input S such that δ(X, S) and δ(Y, S) are (k-1)-distinguishable. Step 3: If Pk ≠ Pk-1, repeat Step 2, otherwise go to Step 4. Step 4: Combine kth equivalent sets and make them the new states of the reduced DFA.ExampleLet us consider the following DFA:
Figure5 example of DFALet us apply Algorithm 3 to the above DFA:
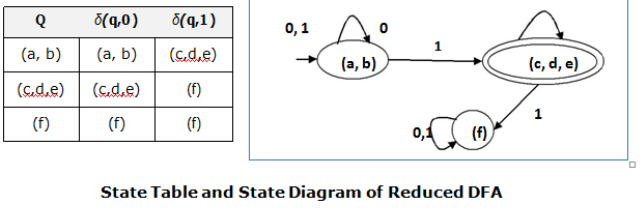
Figure 6 State Table and State Diagram of Reduced DFA References: Introduction to Automata Theory, Languages, and Computation, 2e by John E, Hopcroft, Rajeev Motwani, Jeffery D. Ullman , Pearson Education Theory of Computer Science (Automata, Languages and Computation), 2e by K. L. P. Mishra and N. Chandrasekharan, PHI
|
· P0 = {(c,d,e), (a,b,f)}
· P1 = {(c,d,e), (a,b),(f)}
· P2 = {(c,d,e), (a,b),(f)}
Hence, P1 = P2. There are three states in the reduced DFA. The reduced DFA is as follows:
|
0 matching results found
Browse by Topics