UNIT 1
Introduction
Basically algorithm is the finite steps to solve problem in computer.
It can be the set of instruction than performs certain task.
The collection of unambiguous instruction occurring in some specific sequence and such a procedure should produce output for a given set of input in finite amount of time is known as Algorithm.
1.3 Specification of Algorithm
It is formal way to speak about functions and classify them.
It is used to specify the running time and space complexity of algorithm and to frame the run time performance in mathematical computation.
It refers as boundation or framing into the mathematical terms.
As the algorithm having three cases according to time taken by program to perform a certain task.
Following are the asymptotic notations which are used to calculate the running time complexity of algorithm:
Big Oh Notation (O)
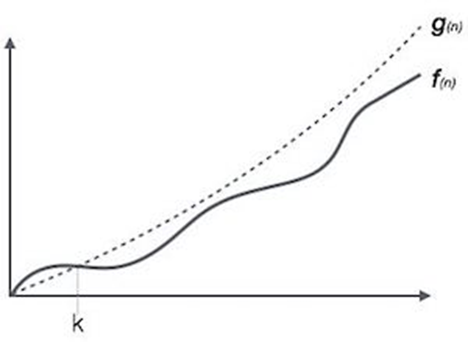
Here, f( n ) <= g( n ) ……………..(eq1)
where n>= k , C>0 and k>=1
if any algorithm satisfies the eq1 condition then it becomes f ( n )= O ( g ( n ) )
Big Omega (ῼ) Notation
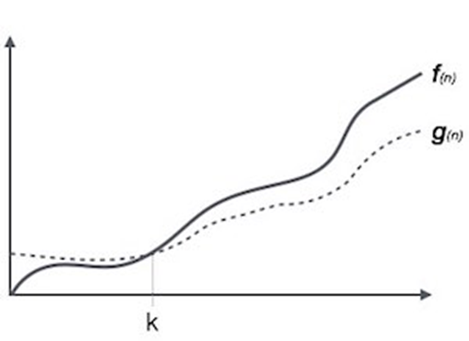
Here, f ( n ) >= g ( n )
where n>=k and c>0, k>=1
if any algorithm satisfies the eq1 condition then it becomes f ( n )= ῼ ( g ( n ) )
Theta (Ꙫ) Notation
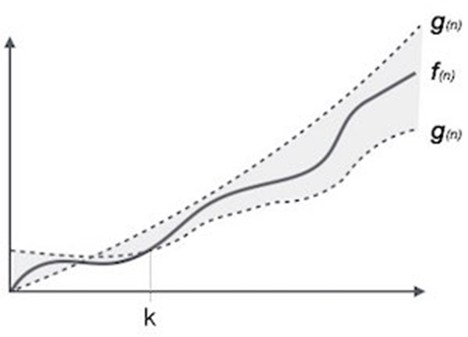
Let C1 g(n) be upper bound and C2 g(n) be lower bound.
C1 g(n)<= f( n )<=C2 g(n)
Where C1, C2>0 and n>=k
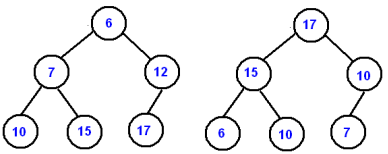
Heap is the special tree based data structure in which it has to satisfy the condition of complete binary tree.
Following are two types of heap:
Max-heap: in this key present at root node must be greater among all key present at all of its children.
Min-heap: in this key present at root node must be minimum among all key present at all of its children.