UNIT 2

Divide & Conquer

2.1 Divide and conquer

Divide & conquer is efficient algorithm.

It follows three steps:

•         divide problem into sub problems

•         Solve each sub problem recursively

Combine all solutions of sub problem to get original solution

2.2 Binary Search Algorithm

•         It is the searching method where we search an element in the given array

•         Method starts with the middle element.

•         if the key element is smaller than the middle element then it searches the key element into first half of the array ie. Left sub-array.

•         If the key element is greater than the middle element then it searches into the second half of the array ie. Right sub-array.

•         This process continues until the key element is found. If there is no key element is present in the given array than it searches fail.

Example: 1,2,3,4,5,6,7,8

Sol:

The given list of elements are:

index

lowhigh

Searching key element 7:

First calculate middle element.

Mid = (low + high)/2 = (0 +8) /2 = 4

Index

                    Low                          mid                                                 high

                                      First half                             second half

Now, searching key is 7

Hence second half will be search.

Low                                          high

Mid= (5+8)/2=6

Now, mid=key element

Here the search key is found at position 6.

2.3 Merge Sort Algorithm

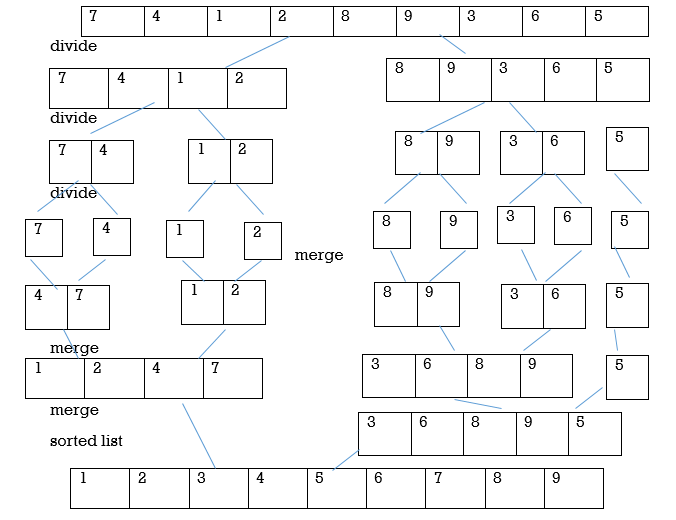
•         Merge sort consisting two phases as divide and merge.

•         In divide phase, each time it divides the given unsorted list into two sub list until each sub list get single element then sorts the elements.

•         In merge phase, it merges all the solution of sub lists and find the original sorted list.  

Steps to solve the problem:

Step 1: if the length of given array is 0 or 1 then it is already sorted else follow step 2.

Step 2: split the given unsorted list into two half parts

Step 3: again divide the sub list into two parts until each sub list get single element

Step 4: As each sub list gets the single element compare all the elements with each other & swap in between the elements.

Step 5: merge the elements same as divide phase to get the sorted list.

Example:

Given unsorted list:

2.4  Analysis of merge sort

All cases having same efficiency as:  O (n log n)

T (n) =T ( n / 2 ) + O ( n )

T (1) = 0

Space requirement:  O (n)

2.5 Quick Sort Algorithm

•         Quick sort algorithm works on the pivot element.

•         Select the pivot element (partitioning element) first. Pivot element can be random number from given unsorted array.

•         Sort the given array according to pivot as the smaller or equal to pivot comes into left array and greater than or equal to pivot comes into right  array.

•         Now select the next pivot to divide the elements and sort the sub arrays recursively.

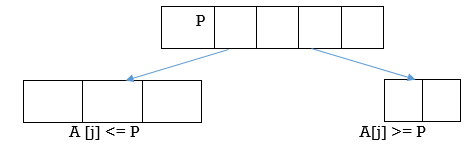
Algorithm:

Given array A [p…….r]Two sub arrays be A [p…q] and A [q+1…….r]

Example

2.6 Analysis of Quick Sort Algorithm

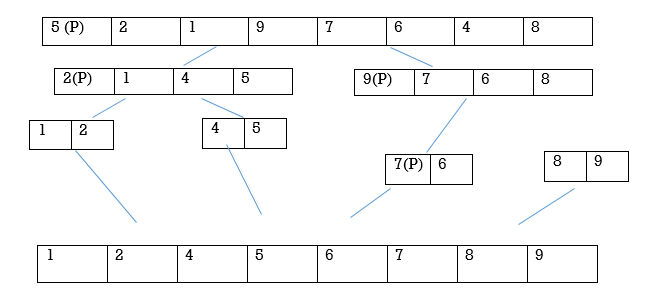
•         Best case: The pivot which we choose will always be swapped into the exactly the middle of the list. And also consider pivot will have an equal number of elements both to its left and right sub arrays.

•         Worst case: Assume that the pivot partition the list into two parts, so that one of the partition has no elements while the other has all the other elements.

•         Average case: Assume that the pivot partition the list into two parts, so that one of the partition has no elements while the other has all the other elements.