UNIT 3

THE GREEDY METHOD

3.1 Greedy Method

Greedy method is same as dynamic programming but difference is that solution of each sub problem is not known to the other sub problems.

It used to solve the optimization problems.

3.2 Fractional Knapsack Problem

Example:

Find optimal solution for knapsack problem where n=7,m=15

No. of object=7

Capacity (m)= 15

Method 1: select object with maximum profit (Pi)

Method 2:Select object with minimum weight(Wi)

Method 3: Select object with maximum profit (Pi) and weight(Wi)

Hence with the help of profit approach, profit/ weight is the best method ie. Method 3.

Analysis:

If the given items are in decreasing sorted manner ie. Order of Pi, Wi and PiWi, then the time taken is O(n).Hence total time for sorting is O(n log n).

3.3    Job Sequencing Algorithm

In job sequencing problem, the objective is to find a sequence of jobs, which is completed within their deadlines and gives maximum profit.

Example:

For the following sequence give the snapshot of execution which will achieve maximum profit

Step 1: sort the job in descending order other profit value.

Select maximum deadline D=4

0             1            2             3           4

Select job J7=30 D=2

 0            1            2             3            4   

P=30

D=2

Select job J3=20 D=4        

0            1            2             3            4   

 P=30      P=20

 D=2         D=4

Select job J4=18 D=3         

0            1            2             3            4   

 P=30      P=20      P=18

D=2         D=4       D=3

Select job J6=6 D=1         

0            1            2             3            4   

P=30      P=20     P=18       P=6

D=2         D=4      D=3         D=1

Total profit=30+20+18+6=74

Job sequence=J7-J3-J4-J6

3.4 Prim’s Algorithm

•         Prim’s algorithm is used to find minimum spanning tree using greedy approach.

•         Spanning tree means the all nodes in the network are connected to each other with minimum possible number of edges.

•         It works on shortest path first technique.

•         Steps to solve the prims algorithm:

Step 1: remove all loops and parallel edges

Step 2:  chose any arbitrary node as root node

Step 3: check the outgoing edeges and chose edge with the less value

Step 4: find the optimal solution by adding all the minimum cost of edges.

Example:

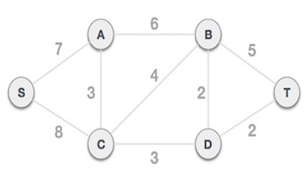
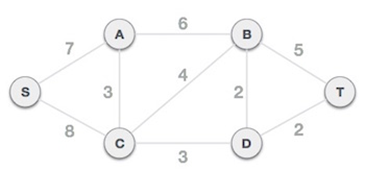
Step 1 - Remove all loops and parallel edges

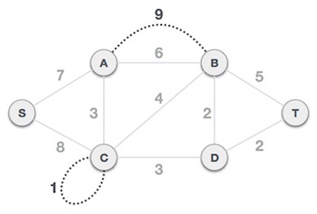
Step 2 - Choose any arbitrary node as root node

All nodes are connect4de to each other in spanning tree hence any node can be the root node. In this example we choose S as root node.

Step 3 - Check outgoing edges and select the one with less cost

Outgoing egeds from s are: S  ->  A  with weight 7 and S -> C with weight 8

SA having minimum weight hence we choose the SA.

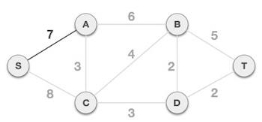
Now, the tree S-A with 7 is remarked as selected path and we check for all edges going out from it.

Now we check all outgoing nodes from A and select the lesser weight edge.

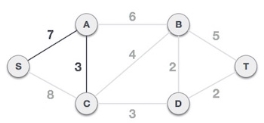
Process continues until we remarked all nodes as visited nodes.

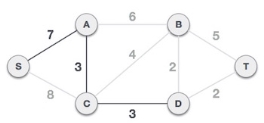
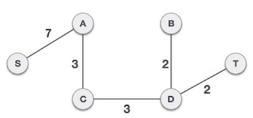
At last we sum all weight to get optimal solution for spanning tree.

Hence solution =7+3+3+2+2=17

3.5  Kruscal’s Algorithm

•         Kruskal’s algorithm is used to find minimum spanning tree same as prims algorithm but difference is it does not lose the properties of spanning tree and selects the edge with least weight from all available edges.

•         It consider the network as forest and every node as individual tree.

Steps to solve the kruscal’s algorithm:

Step 1: remove all loops and parallel edges

Step 2: arrange all edges with its weights in increasing order

Step 3: select the edge with least value among available edges

Step 4: sum up all the edges selected in spanning tree to get the optimal solution

Example:

Step 1 - Remove all loops and Parallel Edges

Remove all loops and parallel edges from the given graph.

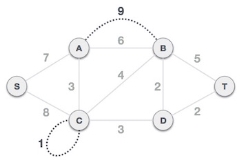
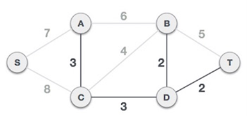
Step 2 - Arrange all edges with its weights in increasing order

The next step is to create a set of edges and weight, and arrange them in an ascending order of weightage (cost).

Step 3 - select the edge with least value among available edges

Select edge with the least weight.

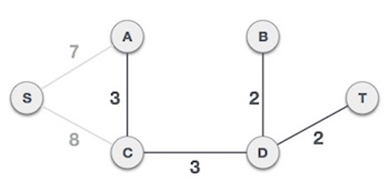
Check the spanning trees properties. If any edge which does not follow the property of spanning tree we will marked that edge as rejected edge.

Now least weight edge s are BD and DT with value 2, select them and checks the properties of spanning tree.

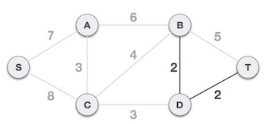
Similarly, continues the process until we get the optimal spanning tree with least weighted

edges.

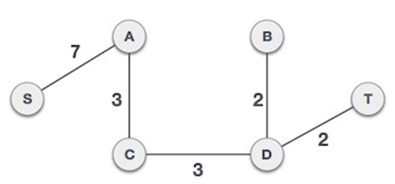
Hence we obtain the optimal solution by adding the edges present in final spanning tree.

Optimal solution=7+3+3+2+2=17

3.6  Dijikstra’sAlgorithm(Single Source Shortest Path)

•         Dijkstra’s algorithm is same as prims algorithm which uses the greedy approach.

•         Difference in prims and Dijkstra’s is Dijkstra’salalgorithm generates the shortest path tree with given root node.

•         It consist of two sets

•         Visited nodes

•         Not visited nodes

•         At every stage ,remark the nose as visited or not visited with its value.

Steps to solve the Dijkstra’salgoithm

Step 1: select the root node

Step 2: firstly, remark all nodes as not visited nodes and place ∞.

Step 3: from the root note check the connecting nodes and marked as visited nodes. Those nodes are not visited by root node remarked as ∞.

Hence the shortest path from root node to all other nodes is 15.

3.7 Optimal Storage Problem on Tapes

Greedy method id used to solve the optimal storage problem.

Following is the example given on it.

Input: We are given ‘n’ problem that are to be stored on computer tape of length L and the length of program i is Li

Such that 1 ≤i≤ n and Σ 1≤k≤j Li≤ 1

Output: A permutation from all n! For the n programs so that when they are stored on tape in the order the MRT is minimized.

Example:

Let n = 3, (l1, l2, l3) = (8, 12, 2). As n = 3, there are 3! =6 possible ordering.

All these orderings and their respective d value are given below:

The optimal ordering is 3, 1, 2.

The greedy method is now applied to solve this problem.

It requires that the programs are stored in non-decreasing order.

The problem is solved in O(n log n) time.

Greedy method solution:

Step 1: Make tape empty

Step 2: For i = 1 to n do;

Step 3: Grab the next shortest path

Step 4: Put it on next tape.

The algorithm takes the best shortest term choice without checking to see whether it is a big long term decision.

Algorithm:

Algorithm ooptimal storage (n,m)

{

K=0;//next tape to be stored

For i=1 to n do

{

Write(i,k);//assign program j to tape k

K=(k+1)mod m;

}

}

For example, find an optimal placement for 13 programs on 3 tapes T0, T1 & T2 where the program are of lengths 12, 5, 8, 32, 7, 5, 18, 26, 4, 3, 11, 10 and 6.

Given problem:

We organize the program as: