UNIT 6
BASIC TRAVERSAL AND SEARCH TECHNIQUES AND POLYNOMIAL PROBLEMS
It is a data structure that is used for data storage purpose.
In the binary tree each node has maximum two children.
It is used to search elements in linked list and ordered array as search becomes as quick in sorted array.
In this tree the insertion and deletion operations are faster in linked list.
Hence it has much benefits in ordered array and linked list.
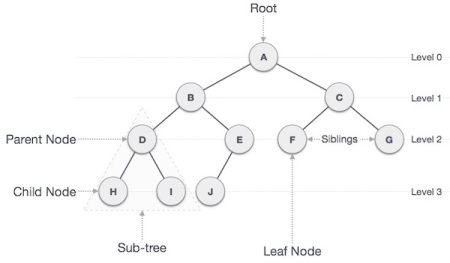
Following figure shows the binary tree where each node contains three components.
The top most node is called as root node and empty tree is represented as null pointer.
Operations on Binary Tree
Insert - inserts an element in tree
Search - searches an element in tree
Delete- deletes an element from tree
It is a directed graph.
It has nodes which are positions in the game and the edges are moves.
It is used in game theory.
The complete game tree is the game where the game tree starts at initial position and contains all possible moves from each position (nodes).
The complete tree becomes when it obtains the extensive from the game representation.
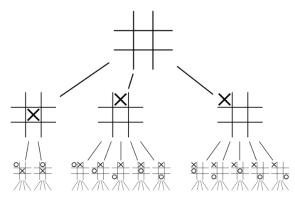
Figure shows the first two levels of the tic-tac-toe game tree.
In the given game tree rotations and the reflections of positions are equivalent hence the first player has three choices of move.
The first player can move it at the center, at the edge or in the corner.
As first player make a move then second player has two choices for the reply.
If the first player played in the center otherwise second player has five choices and so on.
The number of leaf nodes in the complete game tree is the number of possible ways the game can be played.
For example, the game tree for tic-tac-toe has 255,168 leaf nodes.
A) Depth First Search
It is a traversal algorithm which traverse in depthward motion.
It uses the stack to remember and to get the next vertex to search when dead end occurs in any iteration.
Following are some steps that are apply on example.
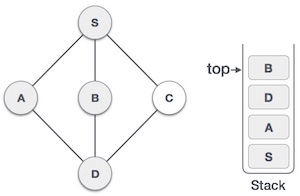
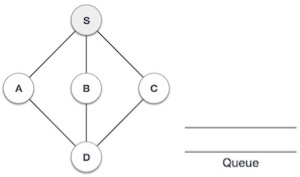
Following is the example for DFS.
Step | Traversal | Description |
1 |
| Initialize the stack which is empty. |
2 |
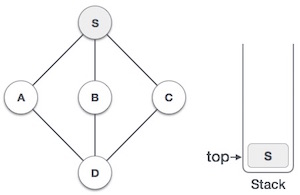
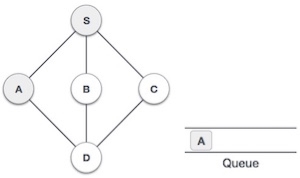
| Mark S as visited and put it onto the stack then take any another unvisited node from S. We will pick A here. You can pick any of three. |
3 |
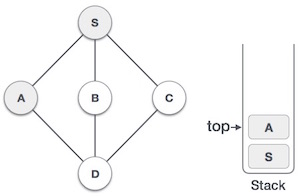
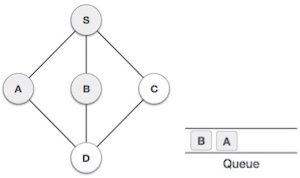
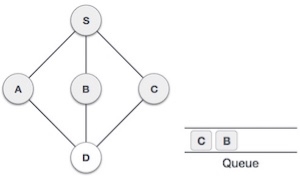
| Mark A as visited and put it onto the stack then explore unvisited node from the node S and A. here A, S, B, C and D are the adjacent nodes. We will visit D. |
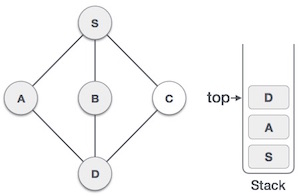
4 |
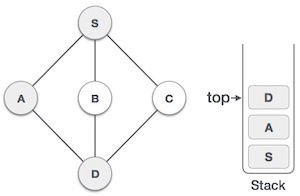
| Visit D and push it in stack and explore another unvisited nodes from D. Next we will visit node B. |
5 |
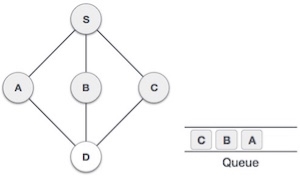
| Visit B push it in stack and go for unvisited node from B but here no adjacent node from B hence pop B from the stack. |
6 |
| Goto to the previous node and find its unvisited node to explore. |
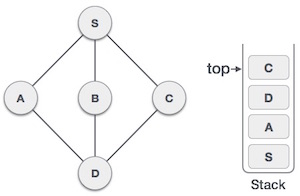
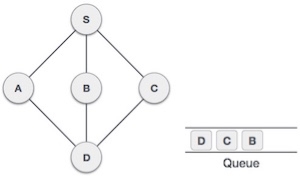
7 |
| Visit C push in the stack. And check for unvisited node. |
As C node is the top of the stack and it does not have any unvisited node then we will keep popping the nodes until we get the unvisited node of any node of the stack.
B) Breadth First Search
BFS is the traversing algorithm.
It is a traversal algorithm which traverse in breadthward motion.
It uses the queue to remember and to get the next vertex to search when dead end occurs in any iteration.
Following are some steps that are apply on example.
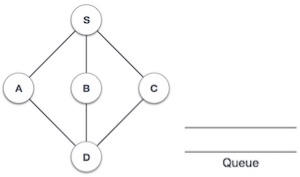
Following is the example for BFS.
Step | Traversal | Description |
1 |
| Initialize the queue i.e. empty. |
2 |
| Start with S. Mark S as visited node. |
3 |
| Check the adjacent unvisited node from S. we will choose A and enqueue it. |
4 |
| The adjacent unvisited node is B from S then mark it as visited and enqueue it.
|
5 |
| The adjacent unvisited node is C from S then mark it as visited and enqueue it.
|
6 |
| Now, all adjacent node from S are visited then dequeue it from queue. Check from A now.
|
7 |
| The adjacent unvisited node is D from A then mark it as visited and enqueue it.
|
Now we are having no unvisited node but we will dequeue all nodes from the queue until queue becomes empty.
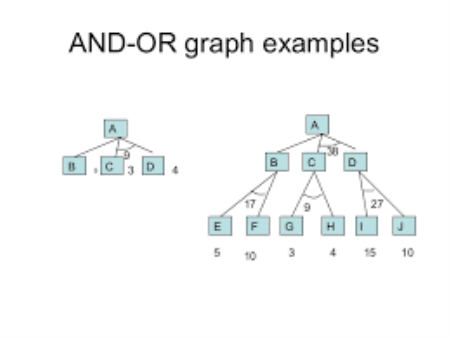
The AND/OR graph is the used to find solution of large problem by decomposing it into smaller problems.
It is useful for representing the solution of problems that can be solved by decomposing them into set of smaller problems.
All that smaller problems must be solved then it gets the solution.
This decomposition generates arcs that all are known as AND arc.
One AND arc may point to the any number of successor node.
All AND arc should be solved in order for the arc to point to a solution.
In OR graph several arcs may emerge from the single node which are indicating a variety of ways in which the original problem might be solved.
This why this graph is known as AND/OR graph.
Example:
The connected component in undirected graph are shown as line by line.
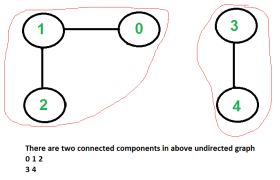
In undirected graph it is easy to find connected components.
To find connected components we need do either BFS or DFS starting from every unvisited vertex.
Following are the algorithm that are used to find strongly connected components in graph.
Kosaraju’s algorithm
Tarjan’s algorithm
It is subset of graph G.
It has all vertices covered with minimum possible number of edges.
Hence spanning tree does not have any cycle and it cannot be disconnected.
Every connected and undirected graph G has at least one spanning tree.
A disconnected graph does not have any spanning tree because of all vertices that are not spanned.
Properties of Spanning Tree:
Application of Spanning Tree:
It is used to find minimum path to connect all nodes in graph.
It is used in civil network planning, computer routing protocol.
It is used to anlyze the cluster.
It is a maximal bi-connected sub-graph.
Bi-connected components are find by following algorithm.
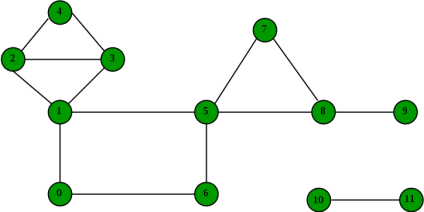
In above graph following are the bi-connected components:
Finding the longest path in graph, etc.