Unit 4
Viewing and Clipping
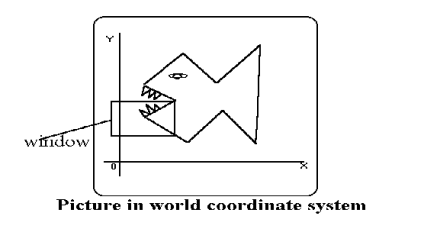
The portion of screen where the selection and enlarging the portion of drawing method is used is called as windowing.
The world coordinates are used to select window.
The window becomes an imaginary box where we select objects or enclose the area of the object.
The size of window is (0,0) coordinates which is bottom left corner and towards the right side until the window encloses the desired area.
The area on display device where the window is mapped is called as viewport.
The viewing transformation is the mapping part of the world coordinate scene to device coordinate.
The viewing transformation is also called as the window to viewport transformation or windowing transformation.
Following figure shows the viewing transformation using standard rectangle for window and viewport.
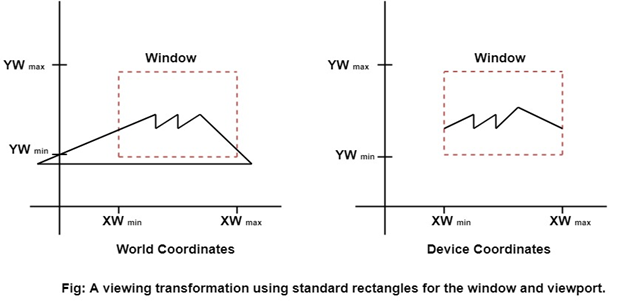
Following are some steps to perform viewing transformation:
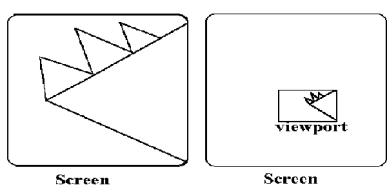
The viewport is a section of screen where the images are encloses by the window on the world coordinate system will be drawn.
When a window is placed on the object and parts of the objects can be seen.
The points and the lines that are outside the window are cut off from view.
This process of cutting off parts of the image on the screen is called as clipping.
In clipping we examine the object with each line that comes completely inside the window, completely outside the window or crosses the window.
If the lines are inside the window then lines will be displayed, if the lines or points are completely outside the window then it is not displayed.
If the line and the points are crosses the window then the part of intersection will be taken and the portion which comes inside the window that will be displayed other part will be not displayed.
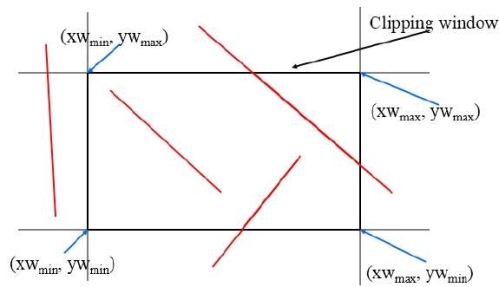
Below figure shows the clipping process.
The clipping of point from the window is very easier than line and polygon clipping.
Following figure shows the point (x,y) is given on the window representing as rectangle.

To clip a point use maximum and minimumcoordinates of the window.
If X- coordinate of point lies in between Wx1 and Wx2 i.e. Wx1<= X <= Wx2 then X coordinate lies inside the window.
If Y- coordinate of point lies in between Wy1 and Wy2 i.e. Wy1<= Y <= Wy2 then Y coordinate lies inside the window.
Line clipping is also same as point clipping.
Here we will cut the portion of line that lies outside the window and keep only the portion that is inside the window.
The line clipping is same as the point clipping method.
The line that is outside the window is cut and the line which is inside the window that will be displayed.
This algorithm uses the line clipping method.
The minimum coordinates for the clipping region is (XWmin, YWmin) and the maximum coordinates are (XWmax, YWmax).
As below figure shows the concept of cohen Sutherland line clipping.
There are three possibilities for line as-
The 4bits are used to divide the entire region.
This 4 bits represents the top, bottom, top and left as the figure shows.
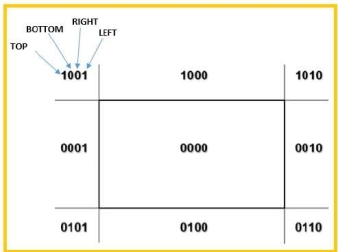
Following are steps to perform the cohen Sutherland algorithm which are based on 4 bits that are given above.
- Choose an endpoints of the line that is outside the window.
- Find the intersection point at the window boundary.
- Replace the endpoints with that intersection points and update the region code.
- Repeat step 2 until we get the clipped line either trivially accepted or trivially rejected.