Unit - 5

Intermediate Code Generation

5.1 Intermediate languages

Intermediate representation in three ways:

1. Syntax tree

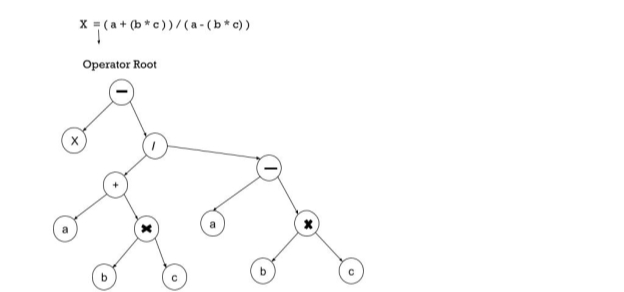
The syntax tree is nothing more than a condensed parse tree shape. The parse tree operator and keyword nodes are transferred to their parents, and in the syntax tree the internal nodes are operators and child nodes are operands, a chain of single productions is replaced by a single connection. Put parentheses in the expression to shape the syntax tree, so it is simple to identify which operand should come first.

Example –

x = (a + b * c) / (a – b * c )

Fig 1: syntax tree

2.     Postfix  notation

The standard way to write the sum of a and b is with the operator in the middle: a + b

For the same expression, the postfix notation positions the operator as ab + at the right end. In general, the consequence of adding + to the values denoted by e1 and e2 is postfix notation by e1e2 +, if e1 and e2 are any postfix expressions, and + is any binary operator.

In postfix notation, no parentheses are needed because the location and arity (number of arguments) of the operators enable only one way of decoding a postfix expression. The operator obeys the operand in postfix notation.

Example –

Representation of a phrase by postfix   (a – b) * (c + d) + (e – f) is  :

ab – cd + *ef -+.

3.     Three address code

Three address statements are defined as a sentence that contains no more than three references (two for operands and one for outcomes). Three address codes are defined as a series of three address statements. The type x = y op z is a three address statement, where x, y, z would have an address (memory location). A statement may often contain fewer than three references, but it is still considered a statement of three addresses.

Example –

The code of the three addresses for the phrase : a + b * c + d :

T 1 = b * c

T 2 = a + T 1

T 3 = T 2 + d

T 1, T 2, T 3  are temporary variables .

Advantages of three address code

●      For target code generation and optimization, the unravelling of complex arithmetic expressions and statements makes the three-address code ideal.

●      Using names for the intermediate values determined by a programme makes it easy to rearrange the three-address code - unlike postfix notation.

Key takeaway :

●      The syntax tree is nothing more than a condensed parse tree shape.

●      In postfix notation, no parentheses are needed because the location and arity of the operators enable only one way of decoding a postfix expression.

●      Three address statements are defined as a sentence that contains no more than three references.

5.2 Declarations

We need to lay out storage for the declared variables when we encounter declarations.

You can manage declaration with a list of names as follows :

D   T id ; D | ε

T   B C | record ‘{‘D’}’

B   int | float

C   ε | [ num ] C

●      A declaration sequence is generated by Nonterminal D.

●      A fundamental, array or record form is generated by nonterminal T.

●      One of the basic int or float types is generated by nonterminal B.

●      Nonterminal C produces a string of zero or more integers, each surrounded by brackets for "component".

We create a ST(Symbol Table) entry for every local name in a procedure, containing:

●      The type of the name

●      How much storage the name requires

Production :

D →    integer, id 

   D  →   real, id 

   D  →   D1, id 

For declarations, an appropriate transformation scheme would be:

ENTER is used to enter the table of symbols and ATTR is used to trace the form of data.

Key takeaway :

●      We need to lay out storage for the declared variables when we encounter declarations.

5.3 Assignment statements and Boolean expressions

Assignment statements allow a symbol to be specified or redefined by the programmer by assigning it a value. This value may be a reference to a different symbol, name of the register, or expression. The new value automatically takes place and remains in effect until the symbol has been redefined. There are no forward connections to symbols specified in assignment statements.

Furthermore, symbols specified in assignment statements are unable to:

Two types of assignment statements exist:

1. Symbol assignment statements

The following syntax is available for a symbol assignment statement:

identifier = expression   // comments

Where,

Identifier = Represents a symbol inside the namespace of the symbol.

Expression = Specifies the identifier's form and meaning. The term cannot contain references forward.

An example of an assignment statement that describes a symbol is below:

S = B0+2

The following syntax is available for a register assignment statement:

identifier = register name   // comments

Where,

Identifier = Represents the name of a register in the name space of the symbol.

Register name = Specifies the name of the alternative register. If the name of the register is a stack or a revolving register name, the current name of the register continues to refer to the previously specified name of the register, even if the name is no longer valid.

An example of an assignment statement that specifies a name for a register is as follows:

B = p1

Boolean Expression

There are two main uses of Boolean expressions. They are used in the estimation of logical values. They are often used when using if-then-else or while-do as a conditional expression.

Consider the grammar

E  →  E OR E 

E  →  E AND E 

E  →  NOT E  

E  →  (E) 

E →  id relop id 

E  →  TRUE 

E  →  FALSE 

The relop is denoted by <, >, <, >.

The AND and OR are still related. NOT has a higher precedent than AND and OR, ultimately.

To generate the three address codes, the EMIT function is used and the newtemp() function is used to generate the temporary variables.

The next state is found in the E →  id relop id2 and provides the index of the next three address statements in the output sequence.

Here is an example of how the three address code is created using the above translation scheme .

p>q AND r<s OR u>r 

     100: if p>q goto 103 

     101: t1:=0 

     102: goto 104 

     103: t1:=1 

     104: if r>s goto 107 

     105: t2:=0 

     106: goto 108 

     107: t2:=1 

     108: if u>v goto 111 

     109: t3:=0 

     110: goto 112 

     111: t3:= 1 

     112: t4:= t1 AND t2 

     113: t5:= t4 OR t3 

Key takeaway :

●      They are often used when using if-then-else or while-do as a conditional expression.

5.4 Case Statements

In a number of languages, the "switch" or "case" statement is available. The syntax for switch-statement is as shown below:

Switch-statement syntax s with expression

begin

   case value : statement

case value : statement

case value : statement

default : statement

end

There is a selector expression to be evaluated, followed by n constant values that may be taken by the expression, including a default value that, if no other value does, always matches the expression. Code to: is the intended translation of a turn.

1. Assess an expression.

2. Find which value is equivalent to the value of the expression in the list of cases.

3. Conduct the assertion that is correlated with the found meaning.

Find the following paragraph about the switch:

switch E

begin

case V1 : S1

case V2 : S2

case Vn-1 : Sn-1

default : Sn

end

This case statement is translated into an intermediate code in the following form: Translation of a case statement.

code to analyze  E into t goto test

goto TEST 

                L1:         code for S1 

                              goto NEXT 

                L2:         code for S2 

                              goto NEXT 

                              . 

                              . 

                              . 

                Ln-1:      code for Sn-1 

                              goto NEXT 

                Ln:         code for Sn 

goto NEXT 

                TEST:      if T = V1 goto L1      

                               if T = V2 goto L2 

                               . 

                               . 

                               . 

                               if T = Vn-1 goto Ln-1 

                               goto  

NEXT: 

A new temporary T and two new label tests are created when the switch keyword is seen, and next.

When the case keyword happens, a new label Li is generated and inserted into the symbol table for each case keyword. A stack is put with the Vi value of each case constant and a pointer to this table-symbol entry.

Key takeaway :

●      Case statement is unique because it contains an expression.

●      Process for switch - case statement

●      Assess an expression.

●      Find which value is equivalent to the value of the expression in the list of cases.

●      Conduct the assertion that is correlated with the found meaning.

5.5 Back patching

All labels can not be recognised in a single pass in the code generation process (primarily, 3 Address Code), so we use a technique called Backpatching.

Backpatching is the task of filling in unspecified label information during the code generation process using acceptable semantic behaviour.

Three functions are used to implement the backpatching technique. The three functions performed in two passes to create code using backpatching are Makelist(), merge() and backpatch().

Three kinds of operations are carried out by Backpatching Algorithms

1. makelist(i) - Creates a new list that contains only an index in the quadruple array, and returns a pointer to the list that it has generated.
2. merge(p1,p2) - This function concatenates lists to which p1 and p2 are pointed, returning a pointer to the list of concatenated ones. This is used for assigning more than one address to the same true / false labels.

3.     backpatch(p,i) - This role is used for the insertion of I as the target mark for each of the The statements in the list which p points to. All statements are attached using the data given by these feature labels.

here ‘p’ is the pointer to any statement say p=> “if a<b goto ____”.

Initially, we don’t know the label to fill just after goto.

After backpatch(p,i)

p=>“if a<b goto i”

Key takeaway :

●      Backpatching is the task of filling in unspecified label information during the code generation process using acceptable semantic behaviour.

●      Three functions are used to implement the backpatching technique.

5.6 Procedure calls

●      Procedure for a compiler is a significant and widely used programming construct. It is used to produce good code for calls and returns for processes.

●      The run-time routines that manage the passing, calling and returning of procedure arguments are part of the packages that support run-time.

Calling sequence :

A series of acts taken on entry and exit from each procedure is part of the translation for a call. In the calling sequence, the following actions take place:

●      When a procedure call occurs, space for the activation record is allocated.

●      Review the so-called method statement.

●      Develop environment pointers to allow data in enclosing blocks to be accessed by the named procedure.

●      Save the state of the calling process so that after the call it can restart execution.

●      Save the return address as well. It is the address of the place to which, after completion, the so-called routine must be moved.

●      Finally, the call procedure creates a hop to the beginning of the code.

let us consider a grammar for a simple procedure call statement

●      S  call id (Elist)

●      Elist  Elist, E

●      Elist  E

For the procedure call, an appropriate transfer scheme would be:

In the procedure call, the queue is used to store a list of parameters.

Key takeaway :

●      It is used to produce good code for calls and returns for processes.

●      A series of acts taken on entry and exit from each procedure is part of the translation for a call.

References :

1. “Compilers - Principles, Techniques and Tools”, A.V. Aho, R. Shethi and J.D.Ullman, Pearson Education

2.     “Compilers - Principles, Techniques and Tools”, A.V. Aho, R. Shethi and J.D.Ullman, Addison Wesley Publishing Company.

3.     “Compiler Construction”, Dhamdere, Mc-Millan.