Unit - 6
Code Generation
Various problems may occur in the code generation phase:
1. Input to the code generator
● The code generator input contains the intermediate representation of the source programme and the symbol table information. The front end creates the source programme.
● The multiple choices have intermediate representation:
- Postfix notation
- Syntax tree
- Three address code
● We assume that the front end generates a low-level intermediate representation, i.e. the system instructions may directly control the values of names in it.
● The code generation stage requires maximum intermediate code that is error-free as required by an input.
2. Target program
The output of the code generator is the target programme. The performance could be:
- Assembly language: It enables the compilation of subroutines separately.
- Relocatable machine language: It makes the code generation process simpler.
- Absolute machine language: It can be stored in memory at a fixed location and can be executed right away.
3. Memory management
● The symbol table entries have to be mapped to individual p addresses during the code generation process and levels have to be mapped to the instruction address.
● The front end and code generator agree with the mapping name in the source programme to address data.
● In the activation record, local variables are stack allocation, while global variables are in the static field
4. Instruction selection
● The design of the target machine's instruction set should be complete and consistent.
● If the performance of the target machine is considered, then the speed of instruction and machine idioms are important considerations.
● Its speed and size will decide the quality of the produced code.
Example:
The Three address code is:
t:= w + x
y:= t + z
Inefficient assembly code is:
MOV w, R0 R0→w
ADD x, R0 R0 x+ R0
MOV R0, t t → R0
MOV t, R0 R0→ t
ADD z, R0 R0 → z + R0
MOV R0, y y → R0
5. Register allocation
The register can be reached more easily than the memory. The instructions for registry operations are shorter and faster than those for memory operations.
When we use registers, the following sub-issues emerge:
- Register allocation: We pick the set of variables in the registry allocation that will reside in the register.
- Register assignment: We choose the register containing a variable in the register assignment
For certain operands and outcomes, certain devices need even-odd pairs of registers.
Example
Consider the form's following division instruction:
D a,b
Where,
a - dividend even register in even/odd register pair
b - divisor
Even register is used to hold the reminder.
Old register is used to hold the quotient.
6. Evaluation order
The effectiveness of the goal code can be influenced by the order in which the calculations are conducted. Some calculation orders require fewer registers than others to carry intermediate data.
Target machine
● For designing a good code generator, familiarity with the target machine and its instruction set is a prerequisite.
● A byte-addressable machine with 4 bytes per word is the target computer.
● It contains n registers for general purposes, R0, R1, . , the Rn-1.
● The form has two address instructions:
op source, destination
Where, op is used as an op-code and the data field is used as source and destination.
● It has the op-codes below :
SUB ( subtract source from destination )
MOV ( move source to destination )
ADD ( add source to destination )
● A combination of registers and memory location with address modes can specify the source and destination of an instruction.
MODE | FORM | ADDRESS | ADDRESS COST |
absolute | M | M | 1 |
register | R | R | 0 |
indexed | c(R) | c+contents(R) | 1 |
indirect register | *R | contents(R) | 0 |
indirect indexed | *c(R) | contents(c+contents(R) ) | 1 |
Example : MOV R0, M, for example, stores Register R0 contents in memory location M.
Instruction costs :
● Instruction cost = 1+ cost for the address modes of source and destination. The duration of the instruction corresponds to this expense.
● The cost of address modes involving registers is zero.
● Address modes that include position or literal memory cost one.
● If space is important, instruction length should be reduced. Doing so often minimises the time taken to fetch the instruction and execute it.
Example : MOV R0, R1, for example, copies the contents of the R0 register to R1. It cost one, because it only occupies one word of memory.
● Via several different instruction sequences, the three-address statement a:= b+c can be implemented:
- MOV b, R0
ADD c, R0 cost = 6 MOV R0,a
b. MOV b, a
ADD c, a cost = 6
c. Assuming that R0, R1 and R2 contain a, b, and c, addresses :
MOV *R1, *R0
ADD *R2, *R0 cost = 2
● We have to use its addressing capabilities effectively to produce good code for the target computer.
Key takeaway :
● The code generator input contains the intermediate representation of the source programme and the symbol table information.
● The code generation stage requires maximum intermediate code that is error-free as required by an input.
● The register can be reached more easily than the memory.
The information needed during a procedure's execution is stored in a storage block called an activation record. The activation record contains storage for local names for the operation.
In the target code, we can define the address using the following methods:
- Static allocation : In static allocation, at compile time, the place of the activation record is fixed in memory.
B. Stack allocation : In stack allocation, a new activation record is moved onto the stack for each execution of a process. Once the activation stops, the record will pop up.
The following three-address statements are correlated with the run-time allocation and deallocation of activation records:
● Call
● Return
● Halt
● Action, a placeholder for other statements
Static allocation
● Implementation of call statement:
The codes needed for static allocation implementation are as follows:
MOV #here + 20, callee.static_area /*It saves return address*/
GOTO callee.code_area /*It transfers control to the target code for the called
procedure */
where,
callee.static_area - Address of the activation record
callee.code_area - Address of the first instruction for called procedure
#here + 20 - Literal return address, which is the address of the following GOTO command.
● Implementation of return statement:
A return from the callee procedure is introduced by: GOTO * callee.static area.
This transfers power to the address that was saved at the start of the activation log.
● Implementation of action statement:
The ACTION instruction is used to execute a declaration of action.
● Implementation of halt statement:
The HALT statement is the final instruction that returns the operating system to power.
Stack allocation
By using relative addresses for storage in activation records, static allocation can become stack allocation. The position of the activation record is stored in the register in the stack allocation, so that words in the activation record can be accessed as offsets from the value in this register.
The codes needed for stack allocation implementation are as follows:
● Initialization of stack:
MOV #stackstart , SP /* initializes stack */
Code for the first procedure
HALT /* terminate execution */
● Implementation of Call statement:
ADD #caller.recordsize, SP /* increment stack pointer */
MOV #here + 16, *SP /*Save return address */
GOTO callee.code_area
Where,
caller.recordsize is the size of the activation record
#here +16 is the address of the instruction following the GOTO
● Implementation of Return statement:
GOTO *0 ( SP ) /*return to the caller */
SUB #caller.recordsize, SP /*decrement SP and restore to previous value */
Key takeaway :
● The information needed during a procedure's execution is stored in a storage block called an activation record.
● The activation record contains storage for local names for the operation.
● In static allocation, at compile time, the place of the activation record is fixed in memory.
● In stack allocation, a new activation record is moved onto the stack for each execution of a process.
The Basic Block includes a declaration sequence. The control flow enters at the beginning of the sentence and leaves without any halt at the end (except may be the last instruction of the block).
A fundamental block is generated by the following sequence of three address statements:
- t1:= x * x
- t2:= x * y
- t3:= 2 * t2
- t4:= t1 + t3
- t5:= y * y
- t6:= t4 + t5
Basic block construction:
Algorithm: Partition into basic blocks
Input : It comprises the series of three sentences of address
Output : It comprises a list of basic blocks in exactly one block with three address statements each.
Method : Identify the leader in the code first. The guidelines are as follows for finding leaders:
● The first statement is a leader.
● Statement L is a leader if the goto statement is conditional or unconditional, such as: if....goto L or goto L
● Instruction L is a leader if a goto or conditional goto sentence like: if goto B or goto B is followed immediately.
The basic block for each leader consists of the leader and all statements up to that. The next leader and the end of the curriculum are not included.
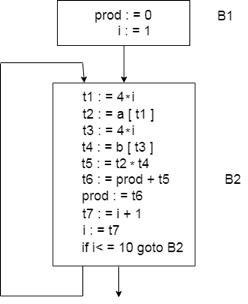
For the dot product of two vectors a and b of length 10, consider the following source code:
begin
prod :=0;
i:=1;
do begin
prod :=prod+ a[i] * b[i];
i :=i+1;
end
while i <= 10
end
The three address codes for the source programme above are given below:
B1
- (1) prod := 0
- (2) i := 1
B2
- (3) t1 := 4* i
- (4) t2 := a[t1]
- (5) t3 := 4* i
- (6) t4 := b[t3]
- (7) t5 := t2*t4
- (8) t6 := prod+t5
- (9) prod := t6
- (10) t7 := i+1
- (11) i := t7
- (12) if i<=10 goto (3)
The basic block B1 contains the declaration (1) to (2)
The basic block B2 contains a declaration (3) to (12)
Flow graph
A directional graph is a flow graph. It contains the control information stream for the basic block collection.
A control flow graph is used to show how the control of the programme between the blocks is parsed. It is helpful in the optimization of the loop.
The vector dot product's flow graph is given as follows:
|
Fig 1: flow graph
● The initial node is block B1. Block B2 follows B1 immediately, so an edge occurs from B2 to B1.
● The jump goal from the last statement of B1 is the first statement of B2, so there is an edge from B1 to B2.
● B2 is a successor to B1 and the precursor to B2 is B1.
Key takeaway :
● The Basic Block includes a declaration sequence.
● A directional graph is a flow graph.
● It contains the control information stream for the basic block collection.
If the name in the register is no longer needed, then the name is deleted from the register and any other names may be stored in the register.
Input: Simple three-address statements block B
Output: We bind to I the liveliness and next-uses of x, y and z at each expression i:x= y op z.
Method: At the last statement of B, we start and search backwards.
● Connect the details currently contained in the symbol table concerning the next-use and liveliness of x, y and z to the statement i.
● Set x to "not live" and "no next use" in the table of symbols.
● Set y to z in the symbol table to "live " and y and z to I in the next use.
Symbol Table |
Names Liveliness Next-use |
X not live no next |
Y live i |
Z live i |
Simple Code Generator
● For a series of three- address statements, a code generator produces target code and uses registers effectively to store statements operands.
● For instance, consider the three-address statement a:= b+c The following sequence of codes can be used:
ADD Rj, Ri Cost = 1
(or)
ADD c, Ri Cost = 2
(or)
MOV c, Rj Cost = 3
ADD Rj, Ri
Register and Address Descriptors :
● To keep track of what is currently in each registry, a registry descriptor is used. The descriptors of the register indicate that all registers are empty initially.
● The address descriptor will store the location where you will find the current value of the name at runtime.
A code-generation algorithm :
● A set of three-address statements constituting a simple block is taken as input by the algorithm. Perform the following behaviour for each three-address declaration of the form x:=y op z:
- Invoke a getreg function to evaluate the position L where the product of the y op z calculation should be stored.
II. To evaluate y ', the present position of y, refer to the address descriptor for y. If the value of y is already both in memory and in a register, choose the register for y '. If the value of y is not already in L, create the MOV command y', L, to put a copy of y in L.
III. Generate the command OP z ', L where z' is the current z position. If z is in both, prefer a register to a memory location. Update the x address descriptor to specify that x is located at position L. Update its descriptor and delete x from all other descriptors if x is in L.
IV. If the current y or z values are no longer used, are not live at the exit of the block and are in registers, change the register descriptor to show that certain registers will no longer contain y or z after execution of x:=y op z.
Generating Code for Assignment Statement :
● The d: = (a-b) + (a-c) + (a-c) assignment can be transformed into the following three-address code sequence,
● In this case, the code sequence is:
t : = a - b
u : = a - c
v : = t + u
d : = v + u
With d live at the end.
Code sequence for the instance is
Statements Code Generated Register descriptor Address descriptor
Register empty
t : = a - b MOV a, R0 R0 contains t t in R0
SUB b, R0
u : = a - c MOV a, R1 R0 contains t t in R0
SUB c, R1 R1 contains u u in R1
v : = t + u ADD R1, R0 R0 contains v u in R1
R1 contains u v in R0
d : = v + u ADD R1, R0 R0 contains d d in R0
MOV R0, d d in R0 and memory
Generating Code for Indexed Statement :
The table displays the generated code sequences for the indexed assignment,
a: = b[ i ] and a[ i ]:= b
Statements Code Generated Cost
a: = b[ i ] MOV b(Ri), R 2
a[ i ]:= b MOV b, a(Ri) 3
Generating Code for Pointer Statement :
The table shows the code sequences generated for the assignments of the pointer,
a : = *p and *p : = a
Statements Code Generated Cost
a : = *p MOV *Rp, a 2
*p : = a MOV a, *Rp 2
Generating Code for Conditional Statement :
if x < 0 goto z ADD z, R0
MOV R0,x
CJ< z
Statement Code
if x < y goto z CMP x, y
CJ < z /* jump to z if condition code is negative*/
x : = y + z MOV y, R0
Key takeaway :
● If the name in the register is no longer needed, then the name is deleted from the register and any other names may be stored in the register.
● For a series of three- address statements, a code generator produces target code and uses registers effectively to store statements operands.
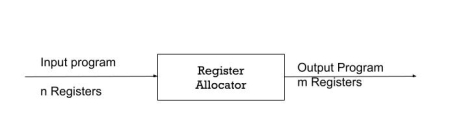
The quickest positions in the hierarchy of memory are registers. But this resource is, unfortunately, small. It falls under the target processor's most restricted tools. Allocation of the register is an NP-complete problem. However, to attain allocation and assignment, this issue can be reduced to graph colouring. An efficient approximate solution to a difficult problem is then determined by a good register allocator.
|
Fig 2: input - output
The allocator of the register specifies the values that will reside in the register and the register that will contain each of those values. It takes a programme with an arbitrary number of registers as its input and generates a programme that can fit into the target machine with a finite register set.
Allocation Vs Assignment
Allocation
Map an infinite namespace to the target machine's register set.
- Register to register model : Digital records are mapped to actual registers, but excess memory spills out.
B. Memory to memory model : Maps any memory location sub-set to a set of names that models the set of physical registers.
Allocation ensures that the code matches the register of the target computer. Put on each instruction.
Assignment
Maps the assigned name set to the target machine physical register set.
● Assumes that the allocation was performed so that the code fits into the physical register set.
● In the registers, no more than 'k' values are specified, where 'k' is the number of physical registers.
Local Register Allocation And Assignment:
Local Reg. is called allocation just inside a simple block. Attribution. Local Reg. Two approaches Allocation: Approach top down and approach bottom up.
The Top Down Approach is a basic 'Frequency Count' approach. Identify the principles that are to be preserved in records and that are to be kept in memory.
Algorithm
- Compute a priority for each virtual register.
- Sort the registers in into priority order.
- Assign registers in priority order.
- Rewrite the code.
Global Register Allocation And Assignment:
- Minimizing the effect of the spill code is the key issue of a register allocator;
● Spill Code execution time.
● Code space for running the spill.
● Data room for values poured out.
II. Global allocation does not guarantee an optimum solution to the spill code execution time.
III. Prime Local and Global Allocation differences:
● Naturally, the composition of a global living range is more complex than that of the local one.
● Within a global live set, a different number of times may be executed for separate references. (When a loop is created by fundamental blocks)
IV. The global allocator mostly uses graph colouring by generating an interference graph to make the decision on allocation and assignments.
V. For that graph, where 'k' is the number of physical registers, the register allocator then attempts to create a k-coloring.
● If the compiler can't create a k-coloring for that graph directly, it modifies the underlying code by pouring some values into memory and then tries again.
● Spilling simply simplifies the graph to ensure that the algorithm stops.
VI. Global Allocator uses various techniques, so we can see top-down and bottom-up strategies for allocation. Subproblems associated with the methods.
● Global Live Ranges Exploration.
● Spilling Expense Estimate.
● Building a Graph of Interference.
Key takeaway :
● There are limited numbers of registers for physical computers
● Typically, preparation and selection presume that infinite registers
● The quickest positions in the hierarchy of memory are registers.
● An efficient approximate solution to a difficult problem is then determined by a good register allocator.
The d:= (a-b) + (a-c) + (a-c) assignment statement can be translated into the following sequence of three address codes:
t:= a-b
u:= a-c
v:= t +u
d:= v+u
Code sequence for the example :
Statement | Code generated | Register descriptor Register empty | Address descriptor |
t:= a - b | MOV a, R0 SUB b, R0 | R0 contains t | t in R0 |
u:= a - c | MOV a, R1 SUB c, R1 | R0 contains t R1 contains u | t in R0 u in R1 |
v:= t + u | ADD R1, R0 | R0 contains v R1 contains u | u in R1 v in R1 |
d:= v + u | ADD R1, R0 MOV R0, d | R0 contains d | d in R0 d in R0 and memory |
Code generation is one of the ideas behind DAG building. Reordering the instructions, marking the nodes with the nodes provide the steps involved.
The number of registers needed to generate the target assembly language code and use this information.
A recursive process on a labelled DAG is used by the code generation algorithm. Based on the labels assigned to the nodes, consider code generation. It uses two stacks, one "rstack" registry stack and one "mstack" memory stack. To assign registers, stack "rstack" is used.
Initially, rstack contains all registers open. The algorithm holds the rstack registers in the same order that it finds them. The standard stack functions, such as push(), pop(), are used to rearrange the rstack, and the algorithm also uses a swap(rstack) function to exchange the rstack's top two registers.
The algorithm considers the generation of code in five separate cases. They are the following:
- Case 0 :This is a simple and terminating situation of the recursive system. If a leaf is 'n' We only generate a load instruction, and the leftmost child of its parent.
2. Case 1 : This is the case where a leaf is the right node and the left node might be a leaf. With sub-tree. In this situation, we generate code to evaluate n1 in register R=top(rstack) followed by the "op name R" command.
3. Case 2 : There are more records needed for the right sub-tree than for the left sub-tree. A sub-tree of the form where n1 can be evaluated without stores, but n2 is more difficult to evaluate than n1 because more records are needed. Swap the top two registers on rsatck for this situation, then evaluate n2 into R=top(rstack). We subtract R from rstack and evaluate n1 into S = top (rstack). We then generate the "op R, S" command that produces the value of "n" in the S register. Another swap call leaves rstack as it was, starting with this generation of call code.
4. Case 3 : It is similar to case 2, except that the left sub-tree is tougher here and is first measured. It is not appropriate to switch registers here.
5. Case 4 : It occurs when r or more registers are needed by both sub-trees to evaluate without the shops. We first evaluate the right subtree into the temporary T, then the left sub-tree, and finally the root, because we have to use a temporary memory spot.
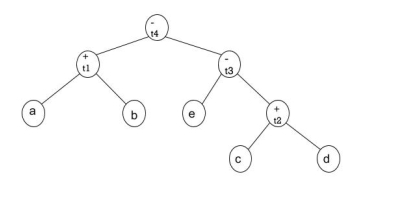
For code generation, consider the DAG given as an example.
|
Fig 3: DAG example
The DAG nodes are labelled with the number of registers needed to be computed. Assume that on the top of the stack there are two registers, R0 and R1, with R0. The root node t4 is used to call the gencode() algorithm. This node's children are t1 and t3. Since t3's label is higher, case 2 is initiated. This calls gencode() recursively with t3 after swapping the Stack of register. This results in a leaf node being its left child and thus comes under case 0. Case 0 is an instruction for loading and the value 'e' is loaded to R1.
It goes to the next one after this call returns the step of the previous call, which uses the pop() command to delete the register R1 from rstack, and the gencode function is called with the correct sub-tree node, t2. This comes under case 1 as the right leaf node mark is 0 and thus the gencode is named again with node 'c'. This comes under case 0 again and initiates a load order into R0 and returns. The next guideline is the
The next step is Case 1 where an operator instruction is issued, followed by the next case 2 instruction where a SUB instruction is issued and the registry is moved and then exchanged.
We get the following code as we continue in a similar way.
Code
gencode(t4) [R1 R0] // case 2
gencode(t3) [R0 R1] // case 3
gencode(e) [R0R1] // case 0
print MOV e, R1
gencode(t2) [R0] // case 1
gencode(c) [R0] // case 0
print MOV c, R0
print ADD d, R0
print SUB R0, R1
gencode(t1) [R0] // case 1
gencode(a) [R0] // case 0
print MOV a, R0
print ADD b, R0
print SUB R1, R0
Key takeaway :
● A recursive process on a labelled DAG is used by the code generation algorithm.
● Based on the labels assigned to the nodes, consider code generation.
● Code generation is one of the ideas behind DAG building.
The Code Generator is used to create the target code for statements with three addresses. It uses registers to store the three address statement operators.
Example : Consider the x:= y + z declaration of three addresses. It can have codes in the following sequence:
MOV x, R0
ADD y, R
Register and Address descriptor :
● A descriptor of a register includes a track of what is in each register at the moment. The descriptors of the register indicate that all the registers are initially empty.
● An address descriptor is used to store the location where you can find the name's current value at runtime.
Generator algorithm
A set of three-address statements is taken as input by the algorithm. The various acts are performed for every three address statements of the form a:= b op c. That are like the following:
- Invoke a getreg function to find out where the output of the b op c calculation should be stored at position L.
II. To decide y ', consult the address definition for y'. If the value of y is currently in memory and both are registered, then the register y' prefers. If the value of y is not already in L, the MOV y ', L command is created to position a copy of y in L.
III. Generate the OP z ', L instruction where z' is used to view the current z position. If z is in both, then a memory location is preferred to a register. Update the x address descriptor to specify that x is located at position L. If x is in L, then the descriptor is modified and x is omitted from all other descriptors.
IV. If the current value of y or z is not used or lives on exit from the block or in the register, change the register descriptor to show that such registers will no longer contain y or z after execution of x:=y op z.
Key takeaway :
● For three-address statements, the code generator is used to generate the target code.
● It uses registers to store the three address statement operands.
● An address descriptor is used to store the location where you can find the name's current value at runtime.
References :
- “Compiler Construction”, Dhamdere, Mc-Millan.
- “Compilers - Principles, Techniques and Tools”, A.V. Aho, R. Shethi and J.D.Ullman, Addison Wesley Publishing Company.
- “Compiler Construction”, Barret, Bates, Couch, Galgotia.