Unit-2
Feedback Characteristics of Control system
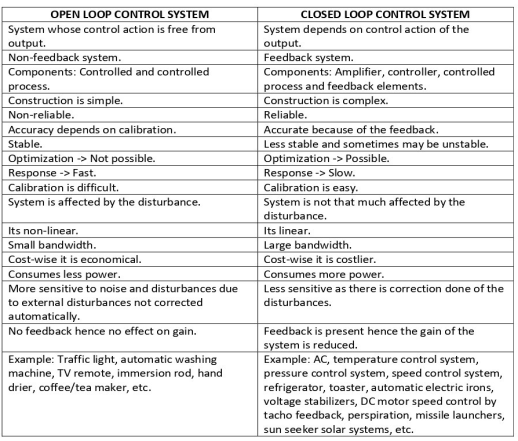
Feedback systems are nothing but closed loop systems and non-feedback systems are open loop systems.
Open loop systems:
This is the loop of control system without any feedback. In this the control action is not dependent on the desired output.
 Fig. 1 open loop control system
Fig. 1 open loop control system
Example of open Loop systems are the traffic signals, Automatic washing machine and in fields control d.c. Motor.
G(s) = c(s)/R(s) -------(1)
Closed loop systems:
This is a type of control system with feedback. In this type of system. The control action is dependent on the desired output.
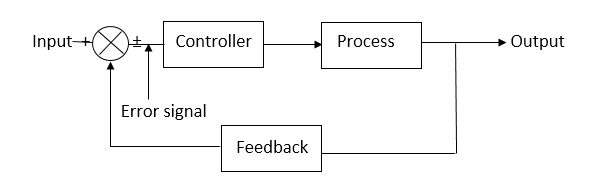 Fig 2 Closed Loop control system
Fig 2 Closed Loop control system
The error signal is again fed to controller to the error and get desired output.
G(s) – forward amplification
H(s) _ Reverse amplification
Above system is with negative feedback.
Positive feedback is used only in oscillators and other use is not known so we discuss only negative feedback systems.
[ R(s) – c(s) H (S) ] G(s) = c(s)
R (s) G(s) = [1+G(s) H(s)] c(s)
C(s)/R(S) = G(S)/1+G(s) H(s)
So, the transfer function of closed Loop system is
C(s)/ R(S) = G(s)/ 1+G(S) H(S) --------(2)
- If numerator of above equation (2) is equalized to zero we get zeros of closed Loop Transfer function [G(S) = 0]
- If dominator of equation (2) is equaled to zero we get polls of the closed loop transfer function [ 1+G(s) H(S) = 0]
1+ G(S) H(s) = 0 [ characteristic Equation]
Stability of the system is determined by the location of its poles.
Key takeaway
The feedback systems are having many advantages over the non-feedback system as we have seen earlier. So, some performance parameters can be controlled through this feedback system such as sensitivity, noise etc. Sensitivity is a parameter which forecasts the effectiveness of feedback in reducing the influence of these variations on system performance. [Reference 4]
The output of the open loop system is given by
C(s) = G(s)R(s)
Now due to variation in parameters G(s) changes to [G(s)+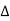 G(s)]. The output will now become
G(s)]. The output will now become
C(s)+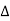 C(s) = [G(s)+
C(s) = [G(s)+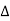 G(s)] R(s)
G(s)] R(s)
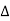 C(s) =
C(s) = 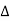 G(s)R(s)
G(s)R(s)
For closed loop system the output is given as
C(s) = 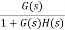 R(s)
R(s)
Now due to variation in parameters it becomes
C(s)+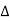 C(s) =
C(s) =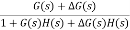 R(s)
R(s)
The above equation shows that if there is variation in parameters then G(s) is reduced by factor of 1+G(s)H(s). The variation in overall transfer function T(s) due to change in G(s) is defined as sensitivity.
Sensitivity = 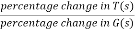
When there is small change in G(s) then sensitivity becomes
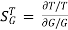
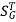 : Sensitivity of T w.r.t G
: Sensitivity of T w.r.t G
For closed loop system the sensitivity will be
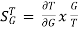 =
= 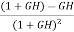 x
x 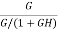 =
= 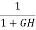
For open loop system
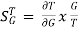 = 1
= 1
As T=G
The sensitivity of T w.r.t H is given as
 =G [
=G [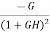 ]
] 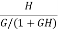 =
= 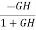
The above equation shows that for large values of GH sensitivity of the feedback system w.r.t H approaches to unity.
Key takeaway
For closed loop system the sensitivity w.r.t G is reduced by a factor of (1+GH) as compared to the open loop system.
The dynamics of the system can be controlled by the feedback by adjusting the location of poles. In this section we will see how the location of poles effect the dynamics of the system.
Let us consider a system which has open loop transfer function of G(s) defined as
G(s) = 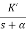 (1)
(1)
Let K = 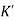 /
/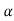
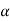 = 1/
= 1/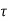
The poles for the above system lie at s= -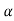 and
and 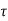 =1/
=1/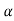 is time constant.
is time constant.
The dc gain of the system is given by G(0) = K = 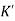 /
/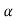
For closed loop system the transfer function is given by
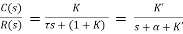 (2)
(2)
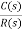 =
= 
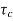 =
=  /(1+K)
/(1+K)
The above equation shows that due to feedback the system pole shifts from -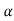 to (–
to (–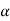 +K’). Due to this change the dynamic response of the system is also affected. For studying the dynamic response, we assume that the input to the system is an impulse.
+K’). Due to this change the dynamic response of the system is also affected. For studying the dynamic response, we assume that the input to the system is an impulse.
r(t) = 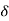 (t)
(t)
And it can also be written as
R(s) = 1
Taking inverse Laplace transform of equation 1 we get
For open loop system
c(t) = K’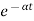
Taking inverse Laplace transform of equation 2 we get
For closed loop system
c(t) = K’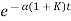
The system dynamic response decays in both the open system as well as closed loop system. The closed loop system time constant is 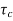 =
= 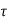 /(1+K) so its response decays faster than open loop system by factor of (1+K).
/(1+K) so its response decays faster than open loop system by factor of (1+K).
Key takeaway
The dynamics of the system can be controlled by the feedback by adjusting the location of poles.
The closed loop system time constant is 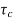 =
= 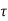 /(1+K) so its response decays faster than open loop system by factor of (1+K).
/(1+K) so its response decays faster than open loop system by factor of (1+K).
The feedback helps to control the disturbances as they generate an error signal. The sfg for closed loop system is given by
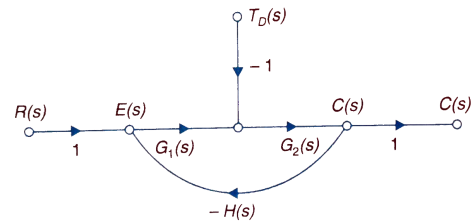
Fig 3 Closed loop system with disturbance signal
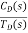 =
= 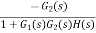
Where:
TD(s) = Disturbance signal.
For |G1G2H(s)|>>1 over the range of s
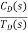 =
=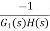
The signal flow graph of a system with noise signal N(s) in the feedback path. The gain is given by
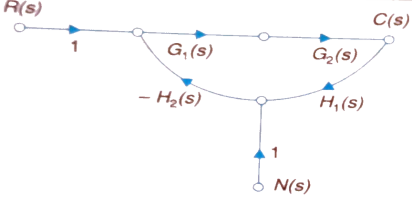
Fig 4 SFG for noise feedback function
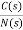 =
= 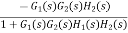
For  >>1
>>1
Cn(s) = 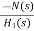
The feedback reduces sensitivity, improves transient response and minimises the effects of disturbance signal in control system.
Concepts of stability
A stable system always gives bounded output for bounded input and the system is known as BIBO stable
A linear time invariant (LTI) system is stable if,
The system is BIBO stable
In absence of the input the output tends towards zero
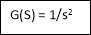
 For system
For system

 1) R(S)
1) R(S)
Fig 5 Control system with G(s) = 1/s2
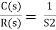
For R(s) = 1
C(S) = 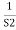
R (t) =  (t) C (t) = t
(t) C (t) = t


 R (t)
R (t) 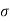 (t)
(t)

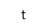
T Bounded Unbounded
Fig 6 Input R(t) Fig 7 Input and output for 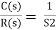
So, system unstable.

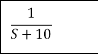

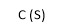 Example 2 R(s)
Example 2 R(s)
[R(s) = 1]
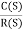 =
= 
C(t) = e-10t C(t)

 t= 0
t= 0
e-10t

e-10t C(t)
 0 t
0 t
1
Fig 8 BIBO stable figure
Routh Hurwitz stability criteria.
It states that the system is stable if and only if all the elements is the first column have the same algebraic sign. If all elements are not of the same sign then the number of sign changes of elements in first column equals the number of roots of the characteristic equation in the right half of S-plane.
Consider the following characteristic equation:
a0 Sn + a1 Sn-1 ………….an = 0 where a0,a1,,,,,,,,,,,,,,,,,,,,an have same sign and are non-zero.
Step1 Arrange coefficients in rows
Row1 ao a2 a4
Row2 a1 a3 a5
Step2 Find third row from above two rows
Row1 a0 a2 a4
Row2 a1 a3 a5
Row3 a1 a3 a5
a1 = 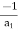
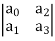 =
= 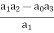
a3 = 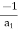
 =
= 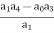
Continue the same procedure to find new rows.
Q1) for the given polynomials below determine the stability of the system
S4+2S3+3S2+4S+5=0
1) Arranging Coefficient in Rows.

S4 | 1 | 3 | 5 |
S3 | 2 | 4 | 0 |
| 1 | 5 | 0 |
| -6 | 0 | 0 |
S0 | 5 | 0 | 0 |
For row S2 first term
S2 = 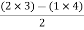 = 1
= 1
For row S2 Second term
S2 = 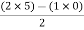 = 5
= 5
For row S1:
S1 = 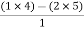 = -6
= -6
For row S0
S0 = 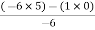 = 5
= 5
As there are two sign change in the first column, So there are two roots or right half of S-plane making system unstable.
Q2. Using Routh criterion determine the stability of the system with characteristic equation S4+8S3+18S2+16S+S = 0
Sol:- Arrange in rows.
| 1 | 18 | 5 |
S3 | 8 | 16 | 0 |
S2 | 16 | 5 |
|
S1 | 13.5 |
|
|
S0 | 5 |
|
|
For row S2 first element
S1 = 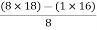 = 16
= 16
Second terms =  = 5
= 5
For S1
First element = 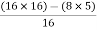 = 13.5
= 13.5
For S0
First element =  = 5
= 5
As there is no sign change for first column so all roots are is left half of S-plane and hence system is stable.
Special Cases of Routh Hurwitz Criterions
- When first element of any row is zero.
In this case the zero is replaced by a very small positive number E and rest of the array is evaluated.
Eg.(1) Consider the following equation
S3+S+2 = 0
| 1 | 1 |
S2 | 0 | 2 |
S1 |
|
|
Replacing 0 by E

S3 | 1 | 1 |
S2 | E | 2 |
S1 | 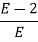 | 0 |
S0 | 2 |
|
Now when E 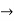 0, values in column 1 becomes
0, values in column 1 becomes
| 1 | 1 |
| E | 2 |
| 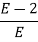 | 0 |
S0 | 2 |
|
Two sign changes hence two roots on right side of S-plans
II) When any one row is having all its terms zero.
When array one row of Routh Hurwitz table is zero, it shown that the X is attests one pair of roots which lies radially opposite to each other in this case the array can be completed by auxiliary polynomial. It is the polynomial row first above row zero.
Consider following example
S3 + 5S2 + 6S + 30
| 1 | 6 |
| 5 |
|
| 0 | 0 |
S0 |
|
|
For forming auxiliary equation, selecting row first above row hang all terms zero.
A(s) = 5S2 e 30
 = 10s e0.
= 10s e0.
Again, forming Routh array
| 1 | 6 |
S2 | 5 | 30 |
S1 | 10 |
|
S0 | 30 |
|
No sign change in column one the roots of Auxiliary equation A(s)=5s2+ 30-0
5s2+30 = 0
S2 α 6= 0
S = ± j 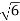
Both lie on imaginary axis so system is marginally stable.
Q3. Determine the stability of the system represent by following characteristic equations using Routh criterion
1) S4 + 3s3 + 8s2 + 4s +3 = 0
2) S4 + 9s3 + 4S2 – 36s -32 = 0
1) S4+3s3+8s2+4s+3=0
S4 | 1 | 8 | 3 |
S3 | 3 | 4 | 0 |
S2 | 6.66 | 3 |
|
S1 | 2.650 | 0 |
|
S0 | 3 |
|
|
No sign change in first column to no rows on right half of S-plane system stable.
S4+9S3+4S2-36S-32 = 0
S4 | 1 | 4 | -32 |
| 9 |
| 0 |
| 8 | -32 |
|
S1 | 0 | 0 |
|
S0 |
|
|
|
Special case II of Routh Hurwitz criterion forming auxiliary equation
A1 (s) = 8S2 – 32 = 0
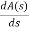 = 16S – 0 =0
= 16S – 0 =0
S4 | 1 | 4 | -32 |
S3 | 9 | -36 | 0 |
S2 | 8 | -32 |
|
| 16 | 0 |
|
S0 | -32 |
|
|
One sign change so, one root lies on right half S-plane hence system is unstable.
Q4. For using feedback open loop transfer function G(s) = 
Find range of k for stability
Soln:- Finding characteristics equation .
CE = 1+G (s) H(s) = 0
H(s) =1 using feedback
CE = 1+ G(s)
1+ 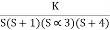 = 0
= 0
S(S+1)(S+3)(S+4)+k = 0
(S2+5)(S2+7Sα12)αK = 0
S4α7S3α1252+S3α7S2α125αK = 0
S4+8S3α19S2+125+k = 0
By Routh Hurwitz Criterion
S4 | 1 | 19 | K |
S3 | 8 | 12 | 0 |
S2 | 17.5 | K |
|
S1 | 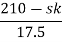 | 0 |
|
S0 | k |
|
|
For system to be stable the range of K is 0< K < 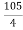 .
.
| 1 | 12 | K |
S3 | 4 | 36 |
|
S2 | 3 | K |
|
S1 |  |
|
|
S0 | K |
|
|
Q5. The characteristic equation for certain feedback control system is given. Find range of K for system to be stable.
Soln
S4+4S3α12S2+36SαK = 0
For stability K>0
 > 0
> 0
K < 27
Range of K will be 0 < K < 27
Relative Stability Criterion:
Routh stability criterion deals about absolute stability of any closed loop system. For relative stability we need to shift the S-plane and the apply the Routh criterion.
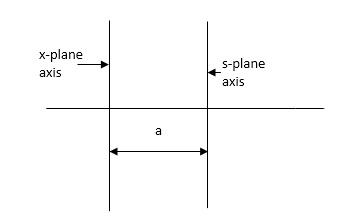
Fig 9 Location of Pole for relative stability
The above fig 9 shows the characteristic equation is modified by shifting the origin of S-plane to S1= -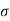 .
.
S = Z-S1
After substituting new valve of S =(Z-S1) applying Routh stability criterion, the number of sign changes in first column is the number of roots on right half of S-plane
Q6. Check if all roots of equation
S3+6S2+25S+38 = 0, have real poll more negative than -1.
Soln:-
S3 | 1 | 25 |
|
S2 | 6 | 38 |
|
S1 | 18.67 |
|
|
S0 | 38 |
|
|

No sign change in first column, hence all roots are in left half of S-plane.
Replacing S = Z-1. In above equation
(Z-1)3+6(Z-1)2+25(Z-1)+38 = 0
Z3+ Z23+16Z+18=0
Z3 | 1 | 16 |
Z2 | 3 | 18 |
Z1 | 10 |
|
Z0 | 18 |
|

No sign change in first column roots lie on left half of Z-plane hence all roots of original equation in S-domain lie to left half of S = -1
Key takeaway
Special Cases of Routh Hurwitz Criterions
- When first element of any row is zero.
In this case the zero is replaced by a very small positive number E and rest of the array is evaluated.
II) When any one row is having all its terms zero.
When array one row of Routh Hurwitz table is zero, it shown that the X is attests one pair of roots which lies radially opposite to each other in this case the array can be completed by auxiliary polynomial. It is the polynomial row first above row zero.
Reference
1 A. Ananadkumar, “Control system Engineering” PHI publication 2nd edition.
2 R. Anandanatarajan, P. Ramesh Babu , “Control Systems Engineering”, Scitech Publications .
3 John R. Hackworth,Fredrick D. Hackworth “ Programmable Logic Controller” Pearson publication.
4 I.J. Nagrath, M.Gopal “Control Systems Engineering”, 5th Edition, New Age International