Unit-5
State Space Analysis
5.1.1 Concept of State
The state of a system is a minimal set of variables known as state variables. The knowledge of these variables at any instance of time together with the knowledge of the inputs for the same instance of time, determines the complete behaviour of the system. The fewer drawbacks in the transfer function method for representing any system led to the use of state variables in analysis of system. Few advantages are listed below:
- The state space can be used for linear or nonlinear, time-variant or time-invariant systems.
- It is easier to apply where Laplace transform cannot be applied.
- The nth order differential equation can be expressed as 'n' equation of first order.
- It is a time domain method.
- As this is time domain method, therefore this method is suitable for digital computer computation.
- On the basis of the given performance index, this system can be designed for an optimal condition.
5.1.2 State Variable and State Model state space representation
The system shown below has ‘m’ inputs, ‘p, outputs and ‘n’ number of state variables. The state equation gives us the relation between the state variables and the inputs.
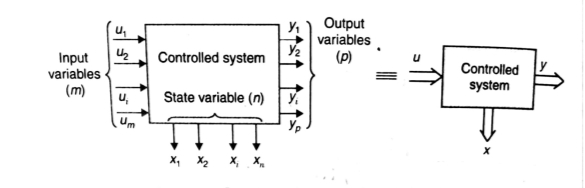
Fig 1 State Variable Representation
So, the above system shown can be described through equations as
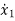 =f1 (x1, x2,…….xn , u1, u2……… ,um)
=f1 (x1, x2,…….xn , u1, u2……… ,um)
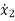 = f2 (x1, x2,…….xn , u1, u2……… ,um)
= f2 (x1, x2,…….xn , u1, u2……… ,um)
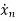 =f1 (x1, x2,…….xn , u1, u2……… ,um) (1)
=f1 (x1, x2,…….xn , u1, u2……… ,um) (1)
The above set of equations can be represented as
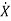 =f(x(t),u(t)) (2)
=f(x(t),u(t)) (2)
As we are concerned for time invariant system, for which the term 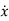 in (1) is linear combination of state variables and input. So,
in (1) is linear combination of state variables and input. So,
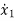 (t)=2tx1+x2+u1+u2 (3)
(t)=2tx1+x2+u1+u2 (3)
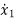 =a11x1(t)+a12x2(t)+…a1nxn(t)+b11u1(t)+b12u2(t)+…….+b1mum(t)
=a11x1(t)+a12x2(t)+…a1nxn(t)+b11u1(t)+b12u2(t)+…….+b1mum(t)
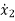 =a21x1(t)+a22x2(t)+…a2nxn(t)+b21u1(t)+b22u2(t)+…….+b2mum(t)
=a21x1(t)+a22x2(t)+…a2nxn(t)+b21u1(t)+b22u2(t)+…….+b2mum(t)
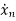 =an1x1(t)+an2x2(t)+…annxn(t)+bn1u1(t)+bn2u2(t)+…….+bnmum(t)
=an1x1(t)+an2x2(t)+…annxn(t)+bn1u1(t)+bn2u2(t)+…….+bnmum(t)
The above equation can be represented in matrix form as given below
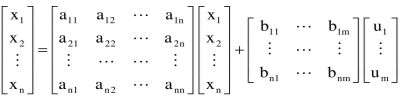 (4)
(4)
The above coefficients aij and bji in equation (4) can be written in vector matrix form as
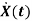 =Ax(t)+Bu(t) (5)
=Ax(t)+Bu(t) (5)
The output of the system can be represented by linear combination of state variables and inputs.
y1=c11x1(t)+c12x2(t)+…….+c1nxn+d11u1+………..+d1mum
y2=c21x1(t)+c22x2(t)+…….+c2nxn+d21u1+………..+d2mum
yr=cr1x1(t)+cr2x2(t)+…….+crnxn+dr1u1+………..+drmum (6)
The equation (6) can be represented in matrix form as 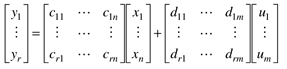 (7)
(7)
Where coefficients cij and dji are constants. The output equation is given as
Y=CX+DU (8)
Key takeaway
The output equation is given as
Y=CX+DU
The state variables in matrix form can be represented as
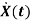 =Ax(t)+Bu(t)
=Ax(t)+Bu(t)
Let the output equation for a state variable be
y(t)=Cx(t)+Du(t)
x(t)=Ax(t)+Bu(t)
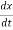 -Ax(t)=Bu(t)
-Ax(t)=Bu(t)
Taking Laplace transform of above equation we get
SX(s)-X(0)-AX(s)=BU(s)
SX(s)-AX(s)=BU(s)+ X (0)
[SI-A]X(s)=X (0) +BU(s)
X(s)=[SI-A]-1[X (0) +BU(s)]
X(s)=[SI-A]-1X (0) +[SI-A]-1BU(s) (9)
This is solution of state differential equation
L-1X(s)= L-1{[SI-A]-1X (0) +[SI-A]-1BU(s)}
x(t)= [SI-A]-1x (0) + [SI-A]-1Bu(t) (10)
From above x(t) we can find output equation by replacing x(t) in output equation by its value from above equation (10)
For the given system below

Fig 2 System with input R(s) and output C(s)
TF=c(t)/r(t)
This c(t) is output of present system, which is not equal to above y(t), as their initial conditions are not considered.
If initial conditions are zero than both y(t) and c(t) will be equal to
L-1[SI-A]-1=φ(t)…….. State transition matrix
Φ(s)=[SI-A]-1
From equation (9)
x(t)=φ(t)x(0)+L-1[φ(s)* BU(s)] (11)
State transition matrix satisfies the solution of state equation when input is zero. [u(t)=0]
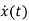 =Ax(t)+Bu(t)
=Ax(t)+Bu(t)
As u(t)=0
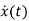 =Ax(t)
=Ax(t)
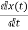 -Ax(t)=0
-Ax(t)=0
Solution to above equation is
y(t)=Ke-Pt+e-Pt∫ ePt Q d(t)
But 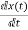 -Ax(t)=0
-Ax(t)=0
Hence above equation becomes
X(t)=AeAt
Substitute t=0
x(0)=ke0
x(0)=k
x(t)=x(0)eAt (zero input response)
Properties of state transition matrix:
From equation (31) when u(t)=0
x(t)=φ(t) x(0)
And from zero input response we have
φ(t)=eAt
Property 1:
φ(0)= [I]
Property 2:
Φ-1(t)= [φ(t)]-1=e-At=eA(-t)
Φ-1(t)= Φ(-t)
Property 3:
ΦK(t)= [Φ(t)]K
ΦK(t)=[eAt]K=eA(tK)
ΦK(t)= Φ(Kt)
Property 4:
Φ(t1+t2)=eA(t1+t2)
=e(At1+At2)=eAt1 * eAt2
Φ(t1+t2)= Φ(t1)Φ(t2)
Property 5:
Φ(t2-t1) * φ(t1-t0)=eA(t2-t1) * eA(t1-t0)
=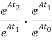
=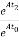 =eA(t2-t0)
=eA(t2-t0)
Φ(t2-t1) * φ(t1-t0)= Φ(t2-t0)
Key takeaway
State transition matrix is given by L-1[SI-A]-1=φ(t)
Zero input response is given by x(t)=x(0)eAt
Practice Problems
Question: A=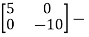 . Find the state transition matrix?
. Find the state transition matrix?
Solution: The state transition matrix is given by L-1[SI-A]-1=φ(t)
[SI-A]=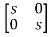
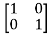 -
-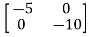
=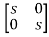 -
-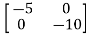
=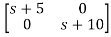
Taking inverse Laplace of above, we get
[SI-A]-1=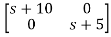 /(S+5)(S+10)
/(S+5)(S+10)
=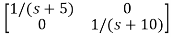
Hence φ(t)=L-1[SI-A]-1=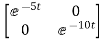
Question: Find state transition matrix if A=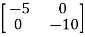
Solution: The state transition matrix is given by L-1[SI-A]-1=φ(t)
[SI-A]=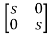 -
-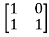
=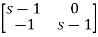
[SI-A]-1=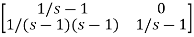
Hence φ(t)=L-1[SI-A]-1=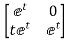
Question: For A=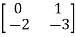 . Calculate characteristic equation and stability?
. Calculate characteristic equation and stability?
Sol: The characteristic equation is given as [SI-A]=0
S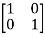 -
- 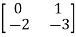 =0
=0
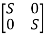 -
-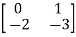 = 0
= 0
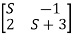 =0
=0
S(S+3)-(-1)*2=0
Hence, the characteristic equation is
S2+3S+2=0
(S+1)(S+2)=0
S=-1,-2
Both roots on left-half of s-plane, real and different, system absolutely stable.
Question: A= 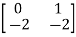 Find the characteristic equation and comment on stability?
Find the characteristic equation and comment on stability?
Sol: The characteristic equation is given by [SI-A] =0
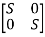 -
-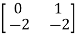 =0
=0
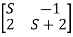 =0
=0
S(S+2)+2=0
S2+2S+2=0
S=-1±j
Roots on left-half of s-plane, complex conjugate, system absolutely stable.
Question: Find f(A)=eAt for A=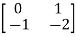
SOL: The characteristic equation is
q(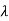 )=|
)=|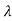 I-A|=
I-A|=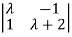 =(
=(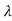 +1)2=0
+1)2=0
The eigen values of A are 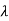 1,
1,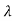 2=-1
2=-1
Since, A is of second order, R(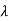 ) will be
) will be
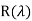 =
=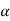 0+
0+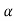 1
1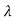
Then 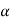 0 and
0 and 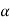 1
1
f(A)=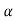 0+
0+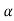 1
1
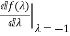 =te-t
=te-t
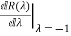 =
=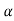 1
1
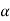 0=(1+t)e-t
0=(1+t)e-t
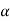 1=te-t
1=te-t
f(A)=eAt=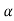 0I+
0I+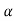 1
1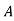
=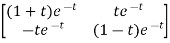
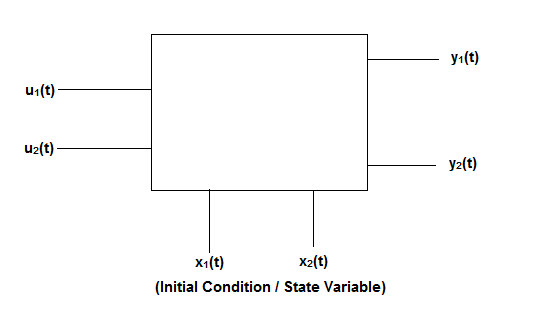
Fig 3: State model
The above figure shows the state model of a system with two inputs u1(t) and u2(t), and having outputs y1(t) and y2(t). As discussed in above section 5.1, we know that the output equation is given as
Y(t)=Cx(t)+Du(t) (12)
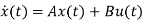 (13)
(13)
Taking L.T of equation (12)
Y(s)=CX(s)+DU(s) (14)
Taking L.T of equation (13)
SX(s)=AX(s)+BU(s) (15)
X(s)=[SI-A]-1BU(s) (16)
Y(s)=CX(s)+DU(s)
Y(s)=C{[SI-A]-1BU(s)} + DU(s)
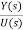 = C{[SI-A]-1B} + D (17)
= C{[SI-A]-1B} + D (17)
[SI-A]-1=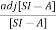
The denominator of equation (17) is the characteristic equation
[SI-A]=0
Key takeaway
The characteristic equation is [SI-A] =0. This equation describes the system stability.
A control system is said to be completely controllable if it’s possible to transfer the state of system from initial state to any other required state.
[S]= [B AB AB2 AB3 ------------------- An-1B]
Kalman’s Test: A system is said to be completely controllable if determinant of matrix is not equal to zero, or the rank of the following matrix should be to ‘n’.
n---- order of the matrix.
If 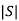 ≠0 then completely controllable
≠0 then completely controllable
If 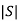 =0 then not controllable
=0 then not controllable
Question: A system is represented by following state model A= 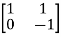 B=
B=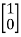 find whether it is controllable or not?
find whether it is controllable or not?
Solution: A= 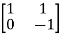 B=
B=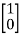
So order of matrix is n=2
[S]=[B AB]
= 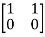
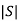 =0 hence, system is not controllable.
=0 hence, system is not controllable.
A system is said to be completely observable if it is possible to determine the initial state of system by observing the output for finite interval of time.
Calman’s Test: A system is said to be completely observable within the determinant of following matrix is not equal to zero, or, the matrix rank should be equal to 1.
[Q]= [CT ATCT (AT)2CT ----------(AT)n-1CT]
If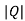 ≠0 then completely observable
≠0 then completely observable
=0 then not observable
Question: A system is represented by following state model A= 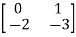 B=
B=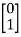 , C=[1 1] test whether the system is observable or not?
, C=[1 1] test whether the system is observable or not?
Solution: AT= 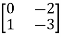 CT=
CT=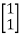
[Q]=[CT ATCT]
=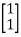
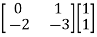
=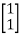
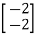
=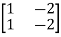
=0
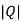 =0 hence not observable.
=0 hence not observable.
Practice Problems
Q1) A system is described by 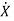 =
=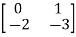 B=
B=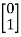 C=[1 0] . Y = [1 0]. Check the controllability of the system?
C=[1 0] . Y = [1 0]. Check the controllability of the system?
Sol: [s] =[B AB]
= 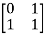
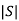 ≠ 0 hence system is controllable.
≠ 0 hence system is controllable.
Q2) A system is described by 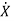 =
=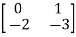 B=
B=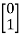 C=[1 0] . Y = [1 0]. Check the observability of the system?
C=[1 0] . Y = [1 0]. Check the observability of the system?
Sol: AT= 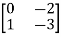 CT=
CT=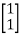
[Q]=[CT ATCT]
=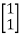
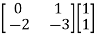
=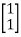
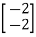
=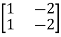
=0
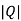 =0 hence not observable.
=0 hence not observable.
Q3) The state equation of the system is given below 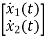 =
= 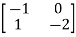
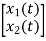 +
+ 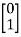 u(t) . Y = [1 2]
u(t) . Y = [1 2]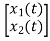 Comment on controllability?
Comment on controllability?
Sol: A= 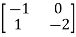 B=
B= 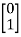
Order of matrix n=2
[S] = [B AB]
=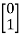
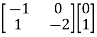
= 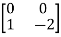
|S|= 0. Hence, system is not controllable.
Q4) The state space representation of a second order 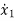 = -x1+u and
= -x1+u and 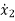 = x1-2x2+u. State whether the system is controllable or not?
= x1-2x2+u. State whether the system is controllable or not?
Sol: 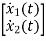 =
= 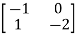
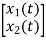 +
+  u(t)
u(t)
Order of matrix is n=2
[S] = [B AB]
=
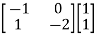
= 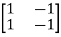
|S|= 0. Hence, system is not controllable.
Q5) A linear second order single input continuous time system is described as 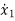 = -2x1(t)+4x2(t) and
= -2x1(t)+4x2(t) and 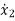 = 2x1(t)-x2(t)+u(t). Comment on controllability?
= 2x1(t)-x2(t)+u(t). Comment on controllability?
Sol: 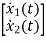 =
= 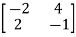
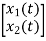 +
+ 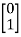 u(t)
u(t)
Order of matrix is n=2
[S] = [B AB]
=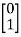
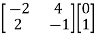
= 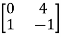
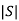 ≠ 0 hence system is controllable.
≠ 0 hence system is controllable.
Reference:
1 A. Ananadkumar, “Control system Engineering” PHI publication 2nd edition.
2 R. Anandanatarajan, P. Ramesh Babu , “Control Systems Engineering”, Scitech Publications .
3 John R. Hackworth,Fredrick D. Hackworth “ Programmable Logic Controller” Pearson publication.
4 I.J. Nagrath, M.Gopal “Control Systems Engineering”, 5th Edition, New Age International