3.1 Introduction linked lists its representation Traversing searching a linked list

Back to Study material

UNIT-3

Linked Lists

3.1 Introduction, linked lists & its representation, Traversing & searching a linked list

Linked List

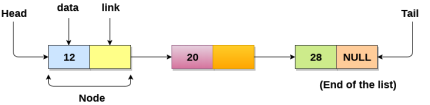
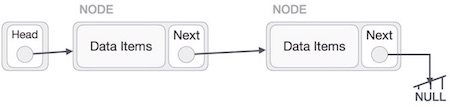
Linked List can be defined as collection of objects called nodes that are randomly stored in the memory.
A node contains two fields i.e. data stored at that particular address and the pointer which contains the address of the next node in the memory.
The last node of the list contains pointer to the null.

DS Linked List

Fig 1 – Linked list

Uses of Linked List

The list is not required to be contiguously present in the memory. The node can reside any where in the memory and linked together to make a list. This achieves optimized utilization of space.
list size is limited to the memory size and doesn't need to be declared in advance.
Empty node can not be present in the linked list.
We can store values of primitive types or objects in the singly linked list.

Why use linked list over array?

Till now, we were using array data structure to organize the group of elements that are to be stored individually in the memory. However, Array has several advantages and disadvantages which must be known in order to decide the data structure which will be used throughout the program.

Array contains following limitations:

The size of array must be known in advance before using it in the program.
Increasing size of the array is a time taking process. It is almost impossible to expand the size of the array at run time.
All the elements in the array need to be contiguously stored in the memory. Inserting any element in the array needs shifting of all its predecessors.

Linked list is the data structure which can overcome all the limitations of an array. Using linked list is useful because,

It allocates the memory dynamically. All the nodes of linked list are non-contiguously stored in the memory and linked together with the help of pointers.
Sizing is no longer a problem since we do not need to define its size at the time of declaration. List grows as per the program's demand and limited to the available memory space.

Singly linked list or One way chain

Singly linked list can be defined as the collection of ordered set of elements. The number of elements may vary according to need of the program. A node in the singly linked list consist of two parts: data part and link part. Data part of the node stores actual information that is to be represented by the node while the link part of the node stores the address of its immediate successor.

One way chain or singly linked list can be traversed only in one direction. In other words, we can say that each node contains only next pointer, therefore we can not traverse the list in the reverse direction.

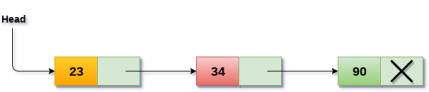
Consider an example where the marks obtained by the student in three subjects are stored in a linked list as shown in the figure.

DS Singly Linked List

Fig 2 - Example

In the above figure, the arrow represents the links. The data part of every node contains the marks obtained by the student in the different subject. The last node in the list is identified by the null pointer which is present in the address part of the last node. We can have as many elements we require, in the data part of the list.

Complexity

Data Structure	Time Complexity								Space Compleity
	Average				Worst				Worst
	Access	Search	Insertion	Deletion	Access	Search	Insertion	Deletion
Singly Linked List	θ(n)	θ(n)	θ(1)	θ(1)	O(n)	O(n)	O(1)	O(1)	O(n)

Operations on Singly Linked List

There are various operations which can be performed on singly linked list. A list of all such operations is given below.

Node Creation

struct node
{
int data;
struct node *next;
};
struct node *head, *ptr;
ptr = (struct node *)malloc(sizeof(struct node *));

Insertion

The insertion into a singly linked list can be performed at different positions. Based on the position of the new node being inserted, the insertion is categorized into the following categories.

SN	Operation	Description
1	Insertion at beginning	It involves inserting any element at the front of the list. We just need to a few link adjustments to make the new node as the head of the list.
2	Insertion at end of the list	It involves insertion at the last of the linked list. The new node can be inserted as the only node in the list or it can be inserted as the last one. Different logics are implemented in each scenario.
3	Insertion after specified node	It involves insertion after the specified node of the linked list. We need to skip the desired number of nodes in order to reach the node after which the new node will be inserted. .

Deletion and Traversing

The Deletion of a node from a singly linked list can be performed at different positions. Based on the position of the node being deleted, the operation is categorized into the following categories.

SN	Operation	Description
1	Deletion at beginning	It involves deletion of a node from the beginning of the list. This is the simplest operation among all. It just need a few adjustments in the node pointers.
2	Deletion at the end of the list	It involves deleting the last node of the list. The list can either be empty or full. Different logic is implemented for the different scenarios.
3	Deletion after specified node	It involves deleting the node after the specified node in the list. we need to skip the desired number of nodes to reach the node after which the node will be deleted. This requires traversing through the list.
4	Traversing	In traversing, we simply visit each node of the list at least once in order to perform some specific operation on it, for example, printing data part of each node present in the list.
5	Searching	In searching, we match each element of the list with the given element. If the element is found on any of the location then location of that element is returned otherwise null is returned. .

Linked List in C: Menu Driven Program

#include<stdio.h>
#include<stdlib.h>
struct node
{
int data;
struct node *next;
};
struct node *head;
void beginsert ();
void lastinsert ();
void randominsert();
void begin_delete();
void last_delete();
void random_delete();
void display();
void search();
void main ()
{
int choice =0;
while(choice != 9)
{
printf("\n\n*********Main Menu*********\n");
printf("\nChoose one option from the following list ...\n");
printf("\n===============================================\n");
printf("\n1.Insert in begining\n2.Insert at last\n3.Insert at any random location\n4.Delete from Beginning\n
5.Delete from last\n6.Delete node after specified location\n7.Search for an element\n8.Show\n9.Exit\n");
printf("\nEnter your choice?\n");
scanf("\n%d",&choice);
switch(choice)
{
case 1:
beginsert();
break;
case 2:
lastinsert();
break;
case 3:
randominsert();
break;
case 4:
begin_delete();
break;
case 5:
last_delete();
break;
case 6:
random_delete();
break;
case 7:
search();
break;
case 8:
display();
break;
case 9:
exit(0);
break;
default:
printf("Please enter valid choice..");
}
}
}
void beginsert()
{
struct node *ptr;
int item;
ptr = (struct node *) malloc(sizeof(struct node *));
if(ptr == NULL)
{
printf("\nOVERFLOW");
}
else
{
printf("\nEnter value\n");
scanf("%d",&item);
ptr->data = item;
ptr->next = head;
head = ptr;
printf("\nNode inserted");
}
}
void lastinsert()
{
struct node *ptr,*temp;
int item;
ptr = (struct node*)malloc(sizeof(struct node));
if(ptr == NULL)
{
printf("\nOVERFLOW");
}
else
{
printf("\nEnter value?\n");
scanf("%d",&item);
ptr->data = item;
if(head == NULL)
{
ptr -> next = NULL;
head = ptr;
printf("\nNode inserted");
}
else
{
temp = head;
while (temp -> next != NULL)
{
temp = temp -> next;
}
temp->next = ptr;
ptr->next = NULL;
printf("\nNode inserted");
}
}
}
void randominsert()
{
int i,loc,item;
struct node *ptr, *temp;
ptr = (struct node *) malloc (sizeof(struct node));
if(ptr == NULL)
{
printf("\nOVERFLOW");
}
else
{
printf("\nEnter element value");
scanf("%d",&item);
ptr->data = item;
printf("\nEnter the location after which you want to insert ");
scanf("\n%d",&loc);
temp=head;
for(i=0;i<loc;i++)
{
temp = temp->next;
if(temp == NULL)
{
printf("\ncan't insert\n");
return;
}
}
ptr ->next = temp ->next;
temp ->next = ptr;
printf("\nNode inserted");
}
}
void begin_delete()
{
struct node *ptr;
if(head == NULL)
{
printf("\nList is empty\n");
}
else
{
ptr = head;
head = ptr->next;
free(ptr);
printf("\nNode deleted from the begining ...\n");
}
}
void last_delete()
{
struct node *ptr,*ptr1;
if(head == NULL)
{
printf("\nlist is empty");
}
else if(head -> next == NULL)
{
head = NULL;
free(head);
printf("\nOnly node of the list deleted ...\n");
}
else
{
ptr = head;
while(ptr->next != NULL)
{
ptr1 = ptr;
ptr = ptr ->next;
}
ptr1->next = NULL;
free(ptr);
printf("\nDeleted Node from the last ...\n");
}
}
void random_delete()
{
struct node *ptr,*ptr1;
int loc,i;
printf("\n Enter the location of the node after which you want to perform deletion \n");
scanf("%d",&loc);
ptr=head;
for(i=0;i<loc;i++)
{
ptr1 = ptr;
ptr = ptr->next;
if(ptr == NULL)
{
printf("\nCan't delete");
return;
}
}
ptr1 ->next = ptr ->next;
free(ptr);
printf("\nDeleted node %d ",loc+1);
}
void search()
{
struct node *ptr;
int item,i=0,flag;
ptr = head;
if(ptr == NULL)
{
printf("\nEmpty List\n");
}
else
{
printf("\nEnter item which you want to search?\n");
scanf("%d",&item);
while (ptr!=NULL)
{
if(ptr->data == item)
{
printf("item found at location %d ",i+1);
flag=0;
}
else
{
flag=1;
}
i++;
ptr = ptr -> next;
}
if(flag==1)
{
printf("Item not found\n");
}
}
}
void display()
{
struct node *ptr;
ptr = head;
if(ptr == NULL)
{
printf("Nothing to print");
}
else
{
printf("\nprinting values . . . . .\n");
while (ptr!=NULL)
{
printf("\n%d",ptr->data);
ptr = ptr -> next;
}
}
}

Output:

*********Main Menu*********

Choose one option from the following list ...

===============================================

1.Insert in begining

2.Insert at last

3.Insert at any random location

4.Delete from Beginning

5.Delete from last

6.Delete node after specified location

7.Search for an element

8.Show

9.Exit

Enter your choice?

Enter value

Node inserted

*********Main Menu*********

Choose one option from the following list ...

===============================================

1.Insert in begining

2.Insert at last

3.Insert at any random location

4.Delete from Beginning

5.Delete from last

6.Delete node after specified location

7.Search for an element

8.Show

9.Exit

Enter your choice?

Enter value?

Node inserted

*********Main Menu*********

Choose one option from the following list ...

===============================================

1.Insert in begining

2.Insert at last

3.Insert at any random location

4.Delete from Beginning

5.Delete from last

6.Delete node after specified location

7.Search for an element

8.Show

9.Exit

Enter your choice?

Enter element value1

Enter the location after which you want to insert 1

Node inserted

*********Main Menu*********

Choose one option from the following list ...

===============================================

1.Insert in begining

2.Insert at last

3.Insert at any random location

4.Delete from Beginning

5.Delete from last

6.Delete node after specified location

7.Search for an element

8.Show

9.Exit

Enter your choice?

printing values . . . . .

*********Main Menu*********

Choose one option from the following list ...

===============================================

1.Insert in begining

2.Insert at last

3.Insert at any random location

4.Delete from Beginning

5.Delete from last

6.Delete node after specified location

7.Search for an element

8.Show

9.Exit

Enter your choice?

Enter value?

123

Node inserted

*********Main Menu*********

Choose one option from the following list ...

===============================================

1.Insert in begining

2.Insert at last

3.Insert at any random location

4.Delete from Beginning

5.Delete from last

6.Delete node after specified location

7.Search for an element

8.Show

9.Exit

Enter your choice?

Enter value

1234

Node inserted

*********Main Menu*********

Choose one option from the following list ...

===============================================

1.Insert in begining

2.Insert at last

3.Insert at any random location

4.Delete from Beginning

5.Delete from last

6.Delete node after specified location

7.Search for an element

8.Show

9.Exit

Enter your choice?

Node deleted from the begining ...

*********Main Menu*********

Choose one option from the following list ...

===============================================

1.Insert in begining

2.Insert at last

3.Insert at any random location

4.Delete from Beginning

5.Delete from last

6.Delete node after specified location

7.Search for an element

8.Show

9.Exit

Enter your choice?

Deleted Node from the last ...

*********Main Menu*********

Choose one option from the following list ...

===============================================

1.Insert in begining

2.Insert at last

3.Insert at any random location

4.Delete from Beginning

5.Delete from last

6.Delete node after specified location

7.Search for an element

8.Show

9.Exit

Enter your choice?

Enter the location of the node after which you want to perform deletion

Deleted node 2

*********Main Menu*********

Choose one option from the following list ...

===============================================

1.Insert in begining

2.Insert at last

3.Insert at any random location

4.Delete from Beginning

5.Delete from last

6.Delete node after specified location

7.Search for an element

8.Show

9.Exit

Enter your choice?

printing values . . . . .

*********Main Menu*********

Choose one option from the following list ...

===============================================

1.Insert in begining

2.Insert at last

3.Insert at any random location

4.Delete from Beginning

5.Delete from last

6.Delete node after specified location

7.Search for an element

8.Show

9.Exit

Enter your choice?

Enter item which you want to search?

item found at location 1

item found at location 2

*********Main Menu*********

Choose one option from the following list ...

===============================================

1.Insert in begining

2.Insert at last

3.Insert at any random location

4.Delete from Beginning

5.Delete from last

6.Delete node after specified location

7.Search for an element

8.Show

9.Exit

Enter your choice?

Searching

Searching is performed in order to find the location of a particular element in the list. Searching any element in the list needs traversing through the list and make the comparison of every element of the list with the specified element. If the element is matched with any of the list element then the location of the element is returned from the function.

Algorithm

Step 1: SET PTR = HEAD
Step 2: Set I = 0
STEP 3: IF PTR = NULL

WRITE "EMPTY LIST"
GOTO STEP 8
END OF IF

STEP 4: REPEAT STEP 5 TO 7 UNTIL PTR != NULL
STEP 5: if ptr → data = item

write i+1
End of IF

STEP 6: I = I + 1
STEP 7: PTR = PTR → NEXT

[END OF LOOP]

STEP 8: EXIT

C function

#include<stdio.h>
#include<stdlib.h>
void create(int);
void search();
struct node
{
int data;
struct node *next;
};
struct node *head;
void main ()
{
int choice,item,loc;
do
{
printf("\n1.Create\n2.Search\n3.Exit\n4.Enter your choice?");
scanf("%d",&choice);
switch(choice)
{
case 1:
printf("\nEnter the item\n");
scanf("%d",&item);
create(item);
break;
case 2:
search();
case 3:
exit(0);
break;
default:
printf("\nPlease enter valid choice\n");
}
}while(choice != 3);
}
void create(int item)
{
struct node *ptr = (struct node *)malloc(sizeof(struct node *));
if(ptr == NULL)
{
printf("\nOVERFLOW\n");
}
else
{
ptr->data = item;
ptr->next = head;
head = ptr;
printf("\nNode inserted\n");
}
}
void search()
{
struct node *ptr;
int item,i=0,flag;
ptr = head;
if(ptr == NULL)
{
printf("\nEmpty List\n");
}
else
{
printf("\nEnter item which you want to search?\n");
scanf("%d",&item);
while (ptr!=NULL)
{
if(ptr->data == item)
{
printf("item found at location %d ",i+1);
flag=0;
}
else
{
flag=1;
}
i++;
ptr = ptr -> next;
}
if(flag==1)
{
printf("Item not found\n");
}
}
}

Output

1.Create

2.Search

3.Exit

4.Enter your choice?1

Enter the item

Node inserted

1.Create

2.Search

3.Exit

4.Enter your choice?1

Enter the item

Node inserted

1.Create

2.Search

3.Exit

4.Enter your choice?2

Enter item which you want to search?

item found at location 1

Key takeaway

Linked List can be defined as collection of objects called nodes that are randomly stored in the memory.
A node contains two fields i.e. data stored at that particular address and the pointer which contains the address of the next node in the memory.
The last node of the list contains pointer to the null.

3.2 Memory allocation

How Memory Management works?

When you declare a variable using a basic data type, the C compiler automatically allocates memory space for the variable in a pool of memory called the stack.

For example, a float variable takes typically 4 bytes (according to the platform) when it is declared. We can verify this information using the sizeof operator as shown in below example

#include <stdio.h>

int main() { float x; printf("The size of float is %d bytes", sizeof(x)); return 0;}

The output will be:

The size of float is 4 bytes

Also, an array with a specified size is allocated in contiguous blocks of memory, each block has the size for one element:

#include <stdio.h>

int main() { float arr[10];

printf("The size of the float array with 10 element is %d", sizeof(arr)); return 0;}

The result is:

The size of the float array with 10 element is 40

As learned so far, when declaring a basic data type or an array, the memory is automatically managed. However, there is a process for allocating memory in C which will permit you to implement a program in which the array size is undecided until you run your program (runtime). This process is called "Dynamic memory allocation."

Dynamic Memory Allocation

Dynamic Memory Allocation is manual allocation and freeing of memory according to your programming needs. Dynamic memory is managed and served with pointers that point to the newly allocated memory space in an area which we call the heap.

Now you can create and destroy an array of elements dynamically at runtime without any problems. To sum up, the automatic memory management uses the stack, and the C Dynamic Memory Allocation uses the heap.

The <stdlib.h> library has functions responsible for Dynamic Memory Management.

Function	Purpose
malloc()	Allocates the memory of requested size and returns the pointer to the first byte of allocated space.
calloc()	Allocates the space for elements of an array. Initializes the elements to zero and returns a pointer to the memory.
realloc()	It is used to modify the size of previously allocated memory space.
Free()	Frees or empties the previously allocated memory space.

Let's discuss the above functions with their application

malloc() Function

The C malloc() function stands for memory allocation. It is a function which is used to allocate a block of memory dynamically. It reserves memory space of specified size and returns the null pointer pointing to the memory location. The pointer returned is usually of type void. It means that we can assign C malloc() function to any pointer.

Syntax of malloc() Function:

ptr = (cast_type *) malloc (byte_size);

Here,

ptr is a pointer of cast_type.
The C malloc() function returns a pointer to the allocated memory of byte_size.

Example of malloc():

Example: ptr = (int *) malloc (50)

When this statement is successfully executed, a memory space of 50 bytes is reserved. The address of the first byte of reserved space is assigned to the pointer ptr of type int.

Consider another example:

#include <stdlib.h>

int main(){

int *ptr;

ptr = malloc(15 * sizeof(*ptr)); /* a block of 15 integers */

if (ptr != NULL) {

*(ptr + 5) = 480; /* assign 480 to sixth integer */

printf("Value of the 6th integer is %d",*(ptr + 5));

}

Output:

Value of the 6th integer is 480

Notice that sizeof(*ptr) was used instead of sizeof(int) in order to make the code more robust when *ptr declaration is typecasted to a different data type later.
The allocation may fail if the memory is not sufficient. In this case, it returns a NULL pointer. So, you should include code to check for a NULL pointer.
Keep in mind that the allocated memory is contiguous and it can be treated as an array. We can use pointer arithmetic to access the array elements rather than using brackets [ ]. We advise to use + to refer to array elements because using incrementation ++ or += changes the address stored by the pointer.

Malloc() function can also be used with the character data type as well as complex data types such as structures.

The free() Function

The memory for variables is automatically deallocated at compile time. In dynamic memory allocation, you have to deallocate memory explicitly. If not done, you may encounter out of memory error.

The free() function is called to release/deallocate memory in C. By freeing memory in your program, you make more available for use later.

For example:

#include <stdio.h>

int main() {

int* ptr = malloc(10 * sizeof(*ptr));

if (ptr != NULL){

*(ptr + 2) = 50;

printf("Value of the 2nd integer is %d",*(ptr + 2));

}

free(ptr);

}

Output

Value of the 2nd integer is 50

calloc() Function

The C calloc() function stands for contiguous allocation. This function is used to allocate multiple blocks of memory. It is a dynamic memory allocation function which is used to allocate the memory to complex data structures such as arrays and structures.

Malloc() function is used to allocate a single block of memory space while the calloc() in C is used to allocate multiple blocks of memory space. Each block allocated by the calloc() function is of the same size.

Syntax of calloc() Function:

ptr = (cast_type *) calloc (n, size);

The above statement is used to allocate n memory blocks of the same size.
After the memory space is allocated, then all the bytes are initialized to zero.
The pointer which is currently at the first byte of the allocated memory space is returned.

Whenever there is an error allocating memory space such as the shortage of memory, then a null pointer is returned.

Example of calloc():

The program below calculates the sum of an arithmetic sequence.

#include <stdio.h>

int main() {

int i, * ptr, sum = 0;

ptr = calloc(10, sizeof(int));

if (ptr == NULL) {

printf("Error! memory not allocated.");

exit(0);

}

printf("Building and calculating the sequence sum of the first 10 terms \ n ");

for (i = 0; i < 10; ++i) { * (ptr + i) = i;

sum += * (ptr + i);

}

printf("Sum = %d", sum);

free(ptr);

return 0;

}

Result:

Building and calculating the sequence sum of the first 10 terms

Sum = 45

calloc() vs. malloc(): Key Differences

Following is the key difference between malloc() Vs calloc() in C:

The calloc() function is generally more suitable and efficient than that of the malloc() function. While both the functions are used to allocate memory space, calloc() can allocate multiple blocks at a single time. You don't have to request for a memory block every time. The calloc() function is used in complex data structures which require larger memory space.

The memory block allocated by a calloc() in C is always initialized to zero while in function malloc() in C, it always contains a garbage value.

realloc() Function

Using the C realloc() function, you can add more memory size to already allocated memory. It expands the current block while leaving the original content as it is. realloc() in C stands for reallocation of memory.

realloc() can also be used to reduce the size of the previously allocated memory.

Syntax of realloc() Function:

ptr = realloc (ptr,newsize);

The above statement allocates a new memory space with a specified size in the variable newsize. After executing the function, the pointer will be returned to the first byte of the memory block. The new size can be larger or smaller than the previous memory. We cannot be sure that if the newly allocated block will point to the same location as that of the previous memory block. This function will copy all the previous data in the new region. It makes sure that data will remain safe.

Example of realloc():

#include <stdio.h>

int main () {

char *ptr;

ptr = (char *) malloc(10);

strcpy(ptr, "Programming");

printf(" %s, Address = %u\n", ptr, ptr);

ptr = (char *) realloc(ptr, 20); //ptr is reallocated with new size

strcat(ptr, " In 'C'");

printf(" %s, Address = %u\n", ptr, ptr);

free(ptr);

return 0;

}

Whenever the realloc() in C results in an unsuccessful operation, it returns a null pointer, and the previous data is also freed.

Dynamic Arrays

A Dynamic array in C allows the number of elements to grow as needed. C Dynamic array are widely used in Computer science algorithms.

In the following program, we have created and resized a Dynamic array in C

#include <stdio.h>

int main() {

int * arr_dynamic = NULL;

int elements = 2, i;

arr_dynamic = calloc(elements, sizeof(int)); //Array with 2 integer blocks

for (i = 0; i < elements; i++) arr_dynamic[i] = i;

for (i = 0; i < elements; i++) printf("arr_dynamic[%d]=%d\n", i, arr_dynamic[i]);

elements = 4;

arr_dynamic = realloc(arr_dynamic, elements * sizeof(int)); //reallocate 4 elements

printf("After realloc\n");

for (i = 2; i < elements; i++) arr_dynamic[i] = i;

for (i = 0; i < elements; i++) printf("arr_dynamic[%d]=%d\n", i, arr_dynamic[i]);

free(arr_dynamic);

}

Result of C Dynamic array program at the screen:

arr_dynamic[0]=0

arr_dynamic[1]=1

After realloc

arr_dynamic[0]=0

arr_dynamic[1]=1

arr_dynamic[2]=2

arr_dynamic[3]=3

Summary

We can dynamically manage memory by creating memory blocks as needed in the heap
In C Dynamic Memory Allocation, memory is allocated at a run time.
Dynamic memory allocation permits to manipulate strings and arrays whose size is flexible and can be changed anytime in your program.
It is required when you have no idea how much memory a particular structure is going to occupy.
Malloc() in C is a dynamic memory allocation function which stands for memory allocation that blocks of memory with the specific size initialized to a garbage value
Calloc() in C is a contiguous memory allocation function that allocates multiple memory blocks at a time initialized to 0
Realloc() in C is used to reallocate memory according to the specified size.
Free() function is used to clear the dynamically allocated memory.

Key takeaway

When you declare a variable using a basic data type, the C compiler automatically allocates memory space for the variable in a pool of memory called the stack.

For example, a float variable takes typically 4 bytes (according to the platform) when it is declared.

3.3 Garbage collection

All the objects which are created dynamically (using new in C++ and Java) are allocated memory in the heap. If we go on creating objects we might get Out Of Memory error, since it is not possible to allocate heap memory to objects. So we need to clear heap memory by releasing memory for all those objects which are no longer referenced by the program (or the unreachable objects) so that the space is made available for subsequent new objects. This memory can be released by the programmer itself but it seems to be an overhead for the programmer, here garbage collection comes to our rescue, and it automatically releases the heap memory for all the unreferenced objects.
There are many garbage collection algorithms which run in the background. One of them is mark and sweep.

Mark and Sweep Algorithm

Any garbage collection algorithm must perform 2 basic operations. One, it should be able to detect all the unreachable objects and secondly, it must reclaim the heap space used by the garbage objects and make the space available again to the program.
The above operations are performed by Mark and Sweep Algorithm in two phases:
1) Mark phase

2) Sweep phase

Mark Phase

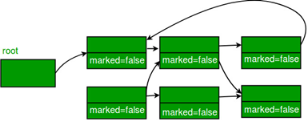
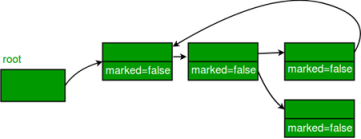
When an object is created, its mark bit is set to 0(false). In the Mark phase, we set the marked bit for all the reachable objects (or the objects which a user can refer to) to 1(true). Now to perform this operation we simply need to do a graph traversal, a DFS approach would work for us. Here we can consider every object as a node and then all the nodes (objects) that are reachable from this node (object) are visited and it goes on till we have visited all the reachable nodes.

Root is a variable that refer to an object and is directly accessible by local variable. We will assume that we have one root only.
We can access the mark bit for an object by: markedBit(obj).

Algorithm -Mark phase:

Mark(root)

If markedBit(root) = false then

markedBit(root) = true

For each v referenced by root

Mark(v)

Note: If we have more than one root, then we simply have to call Mark() for all the root variables.

Sweep Phase

As the name suggests it “sweeps” the unreachable objects i.e. it clears the heap memory for all the unreachable objects. All those objects whose marked value is set to false are cleared from the heap memory, for all other objects (reachable objects) the marked bit is set to true.
Now the mark value for all the reachable objects is set to false, since we will run the algorithm (if required) and again we will go through the mark phase to mark all the reachable objects.

Algorithm – Sweep Phase

Sweep()

For each object p in heap

If markedBit(p) = true then

markedBit(p) = false

else

heap.release(p)

The mark-and-sweep algorithm is called a tracing garbage collector because it traces out the entire collection of objects that are directly or indirectly accessible by the program.

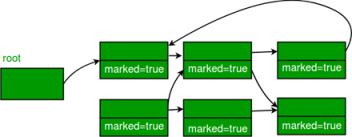
Example:

a) All the objects have their marked bits set to false.

b) Reachable objects are marked true

c) Non reachable objects are cleared from the heap.

Advantages of Mark and Sweep Algorithm

It handles the case with cyclic references, even in case of a cycle, this algorithm never ends up in an infinite loop.
There are no additional overheads incurred during the execution of the algorithm.

Disadvantages of Mark and Sweep Algorithm

The main disadvantage of the mark-and-sweep approach is the fact that that normal program execution is suspended while the garbage collection algorithm runs.
Other disadvantage is that, after the Mark and Sweep Algorithm is run several times on a program, reachable objects end up being separated by many, small unused memory regions. Look at the below figure for better understanding.
Figure:

Fig 3 – Heap Memory

Here white blocks denote the free memory, while the grey blocks denote the memory taken by all the reachable objects.
Now the free segments (which are denoted by white color) are of varying size let’s say the 5 free segments are of size 1, 1, 2, 3, 5 (size in units).
Now we need to create an object which takes 10 units of memory, now assuming that memory can be allocated only in contiguous form of blocks, the creation of object isn’t possible although we have an available memory space of 12 units and it will cause OutOfMemory error. This problem is termed as “Fragmentation”. We have memory available in “fragments” but we are unable to utilize that memory space.
We can reduce the fragmentation by compaction; we shuffle the memory content to place all the free memory blocks together to form one large block. Now consider the above example, after compaction we have a continuous block of free memory of size 12 units so now we can allocate memory to an object of size 10 units.

Key takeaway

3.4 Insertion & deletion of nodes of linked list

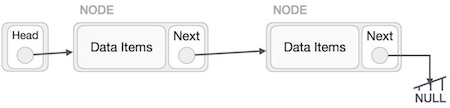
A linked list is a sequence of data structures, which are connected together via links.

Linked List is a sequence of links which contains items. Each link contains a connection to another link. Linked list is the second most-used data structure after array. Following are the important terms to understand the concept of Linked List.

Link − Each link of a linked list can store a data called an element.
Next − Each link of a linked list contains a link to the next link called Next.
LinkedList − A Linked List contains the connection link to the first link called First.

Linked List Representation

Linked list can be visualized as a chain of nodes, where every node points to the next node.

Linked List

Fig 4 - Linked List Representation

As per the above illustration, following are the important points to be considered.

Linked List contains a link element called first.
Each link carries a data field(s) and a link field called next.
Each link is linked with its next link using its next link.
Last link carries a link as null to mark the end of the list.

Types of Linked List

Following are the various types of linked list.

Simple Linked List − Item navigation is forward only.
Doubly Linked List − Items can be navigated forward and backward.
Circular Linked List − Last item contains link of the first element as next and the first element has a link to the last element as previous.

Basic Operations

Following are the basic operations supported by a list.

Insertion − Adds an element at the beginning of the list.
Deletion − Deletes an element at the beginning of the list.
Display − Displays the complete list.
Search − Searches an element using the given key.
Delete − Deletes an element using the given key.

Insertion Operation

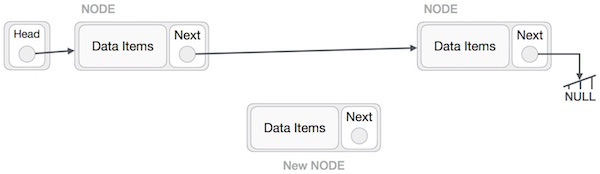
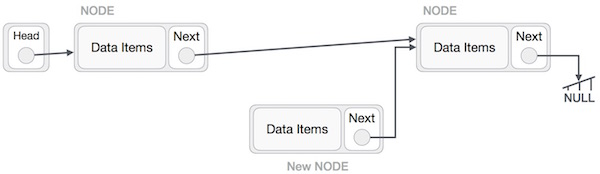
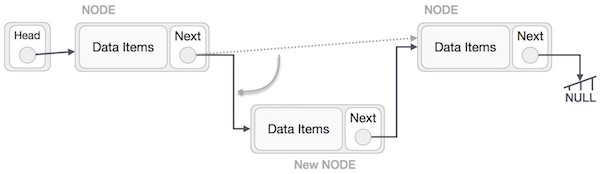
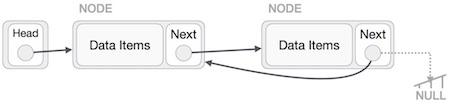
Adding a new node in linked list is a more than one step activity. We shall learn this with diagrams here. First, create a node using the same structure and find the location where it has to be inserted.

Linked List Insertion

Imagine that we are inserting a node B (NewNode), between A (LeftNode) and C (RightNode). Then point B.next to C −

NewNode.next −> RightNode;

It should look like this −

Linked List Insertion

Now, the next node at the left should point to the new node.

LeftNode.next −> NewNode;

Linked List Insertion

This will put the new node in the middle of the two. The new list should look like this −

Linked List Insertion

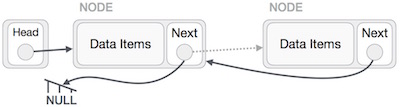
Similar steps should be taken if the node is being inserted at the beginning of the list. While inserting it at the end, the second last node of the list should point to the new node and the new node will point to NULL.

Deletion Operation

Deletion is also a more than one step process. We shall learn with pictorial representation. First, locate the target node to be removed, by using searching algorithms.

Linked List Deletion

The left (previous) node of the target node now should point to the next node of the target node −

LeftNode.next −> TargetNode.next;

Linked List Deletion

This will remove the link that was pointing to the target node. Now, using the following code, we will remove what the target node is pointing at.

TargetNode.next −> NULL;

Linked List Deletion

We need to use the deleted node. We can keep that in memory otherwise we can simply deallocate memory and wipe off the target node completely.

Linked List Deletion

Reverse Operation

This operation is a thorough one. We need to make the last node to be pointed by the head node and reverse the whole linked list.

Linked List Reverse Operation

First, we traverse to the end of the list. It should be pointing to NULL. Now, we shall make it point to its previous node −

Linked List Reverse Operation

We have to make sure that the last node is not the last node. So we'll have some temp node, which looks like the head node pointing to the last node. Now, we shall make all left side nodes point to their previous nodes one by one.

Linked List Reverse Operation

Except the node (first node) pointed by the head node, all nodes should point to their predecessor, making them their new successor. The first node will point to NULL.

Linked List Reverse Operation

We'll make the head node point to the new first node by using the temp node.

Linked List Reverse Operation

A linked list is a sequence of data structures, which are connected together via links. Linked List is a sequence of links which contains items. Each link contains a connection to another link. Linked list is the second most-used data structure after array.

Implementation in C

#include <stdio.h>

#include <string.h>

#include <stdlib.h>

#include <stdbool.h>

struct node {

int data;

int key;

struct node *next;

};

struct node *head = NULL;

struct node *current = NULL;

//display the list

void printList() {

struct node *ptr = head;

printf("\n[ ");

//start from the beginning

while(ptr != NULL) {

printf("(%d,%d) ",ptr->key,ptr->data);

ptr = ptr->next;

}

printf(" ]");

}

//insert link at the first location

void insertFirst(int key, int data) {

//create a link

struct node *link = (struct node*) malloc(sizeof(struct node));

link->key = key;

link->data = data;

//point it to old first node

link->next = head;

//point first to new first node

head = link;

}

//delete first item

struct node* deleteFirst() {

//save reference to first link

struct node *tempLink = head;

//mark next to first link as first

head = head->next;

//return the deleted link

return tempLink;

}

//is list empty

bool isEmpty() {

return head == NULL;

}

int length() {

int length = 0;

struct node *current;

for(current = head; current != NULL; current = current->next) {

length++;

}

return length;

}

//find a link with given key

struct node* find(int key) {

//start from the first link

struct node* current = head;

//if list is empty

if(head == NULL) {

return NULL;

}

//navigate through list

while(current->key != key) {

//if it is last node

if(current->next == NULL) {

return NULL;

} else {

//go to next link

current = current->next;

}

//if data found, return the current Link

return current;

}

//delete a link with given key

struct node* delete(int key) {

//start from the first link

struct node* current = head;

struct node* previous = NULL;

//if list is empty

if(head == NULL) {

return NULL;

}

//navigate through list

while(current->key != key) {

//if it is last node

if(current->next == NULL) {

return NULL;

} else {

//store reference to current link

previous = current;

//move to next link

current = current->next;

}

//found a match, update the link

if(current == head) {

//change first to point to next link

head = head->next;

} else {

//bypass the current link

previous->next = current->next;

}

return current;

}

void sort() {

int i, j, k, tempKey, tempData;

struct node *current;

struct node *next;

int size = length();

k = size ;

for ( i = 0 ; i < size - 1 ; i++, k-- ) {

current = head;

next = head->next;

for ( j = 1 ; j < k ; j++ ) {

if ( current->data > next->data ) {

tempData = current->data;

current->data = next->data;

next->data = tempData;

tempKey = current->key;

current->key = next->key;

next->key = tempKey;

}

current = current->next;

next = next->next;

}

void reverse(struct node** head_ref) {

struct node* prev = NULL;

struct node* current = *head_ref;

struct node* next;

while (current != NULL) {

next = current->next;

current->next = prev;

prev = current;

current = next;

}

*head_ref = prev;

}

void main() {

insertFirst(1,10);

insertFirst(2,20);

insertFirst(3,30);

insertFirst(4,1);

insertFirst(5,40);

insertFirst(6,56);

printf("Original List: ");

//print list

printList();

while(!isEmpty()) {

struct node *temp = deleteFirst();

printf("\nDeleted value:");

printf("(%d,%d) ",temp->key,temp->data);

}

printf("\nList after deleting all items: ");

printList();

insertFirst(1,10);

insertFirst(2,20);

insertFirst(3,30);

insertFirst(4,1);

insertFirst(5,40);

insertFirst(6,56);

printf("\nRestored List: ");

printList();

printf("\n");

struct node *foundLink = find(4);

if(foundLink != NULL) {

printf("Element found: ");

printf("(%d,%d) ",foundLink->key,foundLink->data);

printf("\n");

} else {

printf("Element not found.");

}

delete(4);

printf("List after deleting an item: ");

printList();

printf("\n");

foundLink = find(4);

if(foundLink != NULL) {

printf("Element found: ");

printf("(%d,%d) ",foundLink->key,foundLink->data);

printf("\n");

} else {

printf("Element not found.");

}

printf("\n");

sort();

printf("List after sorting the data: ");

printList();

reverse(&head);

printf("\nList after reversing the data: ");

printList();

}

If we compile and run the above program, it will produce the following result −

Output

Original List:

[ (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) ]

Deleted value:(6,56)

Deleted value:(5,40)

Deleted value:(4,1)

Deleted value:(3,30)

Deleted value:(2,20)

Deleted value:(1,10)

List after deleting all items:

[ ]

Restored List:

[ (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) ]

Element found: (4,1)

List after deleting an item:

[ (6,56) (5,40) (3,30) (2,20) (1,10) ]

Element not found.

List after sorting the data:

[ (1,10) (2,20) (3,30) (5,40) (6,56) ]

List after reversing the data:

[ (6,56) (5,40) (3,30) (2,20) (1,10) ]

Key takeaway

A linked list is a sequence of data structures, which are connected together via links.

Link − Each link of a linked list can store a data called an element.
Next − Each link of a linked list contains a link to the next link called Next.
LinkedList − A Linked List contains the connection link to the first link called First.

3.5 Header linked list

A header node is a special node that is found at the beginning of the list. A list that contains this type of node, is called the header-linked list. This type of list is useful when information other than that found in each node is needed.
For example, suppose there is an application in which the number of items in a list is often calculated. Usually, a list is always traversed to find the length of the list. However, if the current length is maintained in an additional header node that information can be easily obtained.

Types of Header Linked List

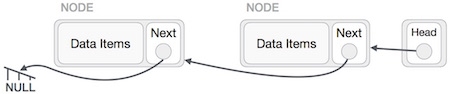
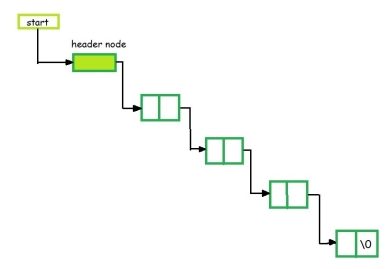
Grounded Header Linked List

It is a list whose last node contains the NULL pointer. In the header linked list the start pointer always points to the header node. start -> next = NULL indicates that the grounded header linked list is empty. The operations that are possible on this type of linked list are Insertion, Deletion, and Traversing.

Fig 5 – Grounded header linked list

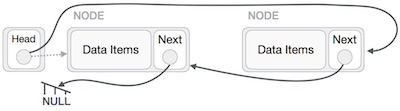
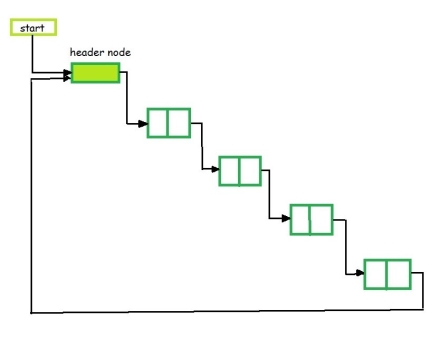
2. Circular Header Linked List

A list in which last node points back to the header node is called circular linked list. The chains do not indicate first or last nodes. In this case, external pointers provide a frame of reference because last node of a circular linked list does not contain the NULL pointer. The possible operations on this type of linked list are Insertion, Deletion and Traversing.

Fig 6 – Circular Header linked list

// C program for a Header Linked List

#include <malloc.h>

#include <stdio.h>

// Structure of the list

struct link {

int info;

struct link* next;

};

// Empty List

struct link* start = NULL;

// Function to create a header linked list

struct link* create_header_list(int data)

{

// Create a new node

struct link *new_node, *node;

new_node = (struct link*)

malloc(sizeof(struct link));

new_node->info = data;

new_node->next = NULL;

// If it is the first node

if (start == NULL) {

// Initialize the start

start = (struct link*)

malloc(sizeof(struct link));

start->next = new_node;

}

else {

// Insert the node in the end

node = start;

while (node->next != NULL) {

node = node->next;

}

node->next = new_node;

}

return start;

}

// Function to display the

// header linked list

struct link* display()

{

struct link* node;

node = start;

node = node->next;

while (node != NULL) {

printf("%d ", node->info);

node = node->next;

}

printf("\n");

return start;

}

// Driver code

int main()

{

// Create the list

create_header_list(11);

create_header_list(12);

create_header_list(13);

// Print the list

display();

create_header_list(14);

create_header_list(15);

// Print the list

display();

return 0;

}

Output:

11 12 13

11 12 13 14 15

Applications of Header Linked List

Polynomials

The header linked lists are frequently used to maintain the polynomials in memory. The header node is used to represent the zero polynomial.
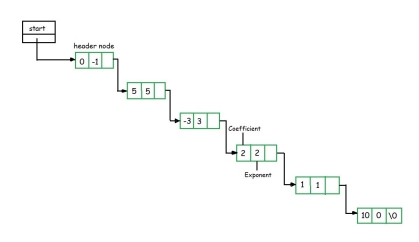
Suppose we have
F(x) = 5x5 – 3x3 + 2x2 + x1 +10x0
From the polynomial represented by F(x) it is clear that this polynomial has two parts, coefficient and exponent, where, x is formal parameter. Hence, we can say that a polynomial is sum of terms, each of which consists of a coefficient and an exponent.
The computer implementation requires implementing polynomials as a list of pair of coefficient and exponent. Each of these pairs will constitute a structure, so a polynomial will be represented as a list of structures.
If one wants to represent F(x) with help of linked list then the list will contain 5 nodes. When we link each node we get a linked list structure that represents polynomial F(x).

Addition of polynomials

To add two polynomials, we need to scan them once.
If we find terms with the same exponent in the two polynomials, then we add the coefficients, otherwise, we copy the term of larger exponent into the sum and go on.
When we reach at the end of one of the polynomial, then remaining part of the other is copied into the sum.
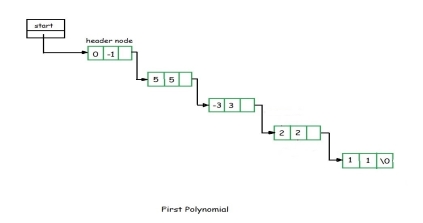
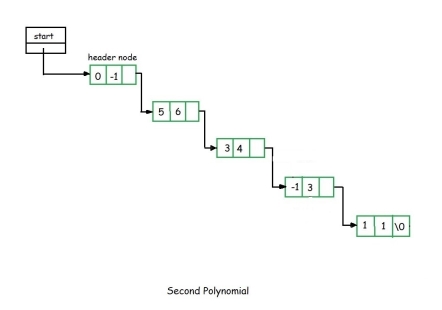
Suppose we have two polynomials as illustrated and we have to perform addition of these polynomials.

5. When we scan first node of the two polynomials, we find that exponential power of first node in the second polynomial is greater than that of first node of the first polynomial.

6. Here the exponent of the first node of the second polynomial is greater hence we have to copy first node of the second polynomial into the sum.

7. Then we consider the first node of the first polynomial and once again first node value of first polynomial is compared with the second node value of the second polynomial.

8. Here the first node exponent value of the first polynomial is greater than the second node exponent value of the second polynomial. We copy the first node of the first polynomial into the sum.

9. Now consider the second node of the first polynomial and compare it with the second node of the second polynomial.

10. Here the exponent value of the second node of the second polynomial is greater than the second node of the first polynomial, hence we copy the second node of the second list into the sum.

11. Now we consider the third node exponent of the second polynomial and compare it with second node exponent value of the first polynomial. We find that both are equal, hence perform addition of their coefficient and copy in to the sum.

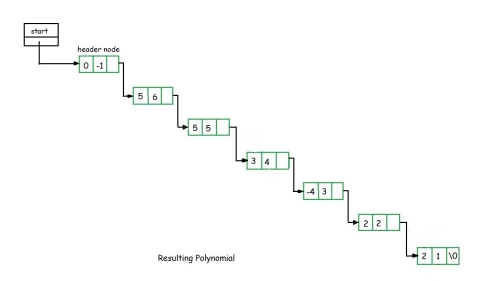
12. This process continues till all the nodes of both the polynomial are exhausted. For example after adding the above two polynomials, we get the following resultant polynomial as shown.

Key takeaway

3.6 Two-way lists

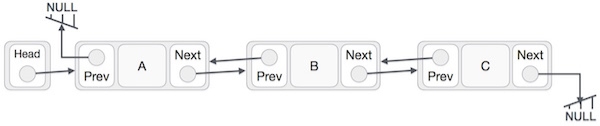
Doubly Linked List is a variation of Linked list in which navigation is possible in both ways, either forward and backward easily as compared to Single Linked List. Following are the important terms to understand the concept of doubly linked list.

Link − Each link of a linked list can store a data called an element.
Next − Each link of a linked list contains a link to the next link called Next.
Prev − Each link of a linked list contains a link to the previous link called Prev.
LinkedList − A Linked List contains the connection link to the first link called First and to the last link called Last.

Fig 7 - Doubly Linked List Representation

Doubly Linked List

As per the above illustration, following are the important points to be considered.

Doubly Linked List contains a link element called first and last.
Each link carries a data field(s) and two link fields called next and prev.
Each link is linked with its next link using its next link.
Each link is linked with its previous link using its previous link.
The last link carries a link as null to mark the end of the list.

Basic Operations

Following are the basic operations supported by a list.

Insertion − Adds an element at the beginning of the list.
Deletion − Deletes an element at the beginning of the list.
Insert Last − Adds an element at the end of the list.
Delete Last − Deletes an element from the end of the list.
Insert After − Adds an element after an item of the list.
Delete − Deletes an element from the list using the key.
Display forward − Displays the complete list in a forward manner.
Display backward − Displays the complete list in a backward manner.

Insertion Operation

Following code demonstrates the insertion operation at the beginning of a doubly linked list.

Example

//insert link at the first location

void insertFirst(int key, int data) {

//create a link

struct node *link = (struct node*) malloc(sizeof(struct node));

link->key = key;

link->data = data;

if(isEmpty()) {

//make it the last link

last = link;

} else {

//update first prev link

head->prev = link;

}

//point it to old first link

link->next = head;

//point first to new first link

head = link;

}

Deletion Operation

Following code demonstrates the deletion operation at the beginning of a doubly linked list.

Example

//delete first item

struct node* deleteFirst() {

//save reference to first link

struct node *tempLink = head;

//if only one link

if(head->next == NULL) {

last = NULL;

} else {

head->next->prev = NULL;

}

head = head->next;

//return the deleted link

return tempLink;

}

Insertion at the End of an Operation

Following code demonstrates the insertion operation at the last position of a doubly linked list.

Example

//insert link at the last location

void insertLast(int key, int data) {

//create a link

struct node *link = (struct node*) malloc(sizeof(struct node));

link->key = key;

link->data = data;

if(isEmpty()) {

//make it the last link

last = link;

} else {

//make link a new last link

last->next = link;

//mark old last node as prev of new link

link->prev = last;

}

//point last to new last node

last = link;

}

Doubly Linked List is a variation of Linked list in which navigation is possible in both ways, either forward and backward easily as compared to Single Linked List.

Implementation in C

#include <stdio.h>

#include <string.h>

#include <stdlib.h>

#include <stdbool.h>

struct node {

int data;

int key;

struct node *next;

struct node *prev;

};

//this link always point to first Link

struct node *head = NULL;

//this link always point to last Link

struct node *last = NULL;

struct node *current = NULL;

//is list empty

bool isEmpty() {

return head == NULL;

}

int length() {

int length = 0;

struct node *current;

for(current = head; current != NULL; current = current->next){

length++;

}

return length;

}

//display the list in from first to last

void displayForward() {

//start from the beginning

struct node *ptr = head;

//navigate till the end of the list

printf("\n[ ");

while(ptr != NULL) {

printf("(%d,%d) ",ptr->key,ptr->data);

ptr = ptr->next;

}

printf(" ]");

}

//display the list from last to first

void displayBackward() {

//start from the last

struct node *ptr = last;

//navigate till the start of the list

printf("\n[ ");

while(ptr != NULL) {

//print data

printf("(%d,%d) ",ptr->key,ptr->data);

//move to next item

ptr = ptr ->prev;

}

//insert link at the first location

void insertFirst(int key, int data) {

//create a link

struct node *link = (struct node*) malloc(sizeof(struct node));

link->key = key;

link->data = data;

if(isEmpty()) {

//make it the last link

last = link;

} else {

//update first prev link

head->prev = link;

}

//point it to old first link

link->next = head;

//point first to new first link

head = link;

}

//insert link at the last location

void insertLast(int key, int data) {

//create a link

struct node *link = (struct node*) malloc(sizeof(struct node));

link->key = key;

link->data = data;

if(isEmpty()) {

//make it the last link

last = link;

} else {

//make link a new last link

last->next = link;

//mark old last node as prev of new link

link->prev = last;

}

//point last to new last node

last = link;

}

//delete first item

struct node* deleteFirst() {

//save reference to first link

struct node *tempLink = head;

//if only one link

if(head->next == NULL){

last = NULL;

} else {

head->next->prev = NULL;

}

head = head->next;

//return the deleted link

return tempLink;

}

//delete link at the last location

struct node* deleteLast() {

//save reference to last link

struct node *tempLink = last;

//if only one link

if(head->next == NULL) {

head = NULL;

} else {

last->prev->next = NULL;

}

last = last->prev;

//return the deleted link

return tempLink;

}

//delete a link with given key

struct node* delete(int key) {

//start from the first link

struct node* current = head;

struct node* previous = NULL;

//if list is empty

if(head == NULL) {

return NULL;

}

//navigate through list

while(current->key != key) {

//if it is last node

if(current->next == NULL) {

return NULL;

} else {

//store reference to current link

previous = current;

//move to next link

current = current->next;

}

//found a match, update the link

if(current == head) {

//change first to point to next link

head = head->next;

} else {

//bypass the current link

current->prev->next = current->next;

}

if(current == last) {

//change last to point to prev link

last = current->prev;

} else {

current->next->prev = current->prev;

}

return current;

}

bool insertAfter(int key, int newKey, int data) {

//start from the first link

struct node *current = head;

//if list is empty

if(head == NULL) {

return false;

}

//navigate through list

while(current->key != key) {

//if it is last node

if(current->next == NULL) {

return false;

} else {

//move to next link

current = current->next;

}

//create a link

struct node *newLink = (struct node*) malloc(sizeof(struct node));

newLink->key = newKey;

newLink->data = data;

if(current == last) {

newLink->next = NULL;

last = newLink;

} else {

newLink->next = current->next;

current->next->prev = newLink;

}

newLink->prev = current;

current->next = newLink;

return true;

}

void main() {

insertFirst(1,10);

insertFirst(2,20);

insertFirst(3,30);

insertFirst(4,1);

insertFirst(5,40);

insertFirst(6,56);

printf("\nList (First to Last): ");

displayForward();

printf("\n");

printf("\nList (Last to first): ");

displayBackward();

printf("\nList , after deleting first record: ");

deleteFirst();

displayForward();

printf("\nList , after deleting last record: ");

deleteLast();

displayForward();

printf("\nList , insert after key(4) : ");

insertAfter(4,7, 13);

displayForward();

printf("\nList , after delete key(4) : ");

delete(4);

displayForward();

}

If we compile and run the above program, it will produce the following result −

Output

List (First to Last):

[ (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) ]

List (Last to first):

[ (1,10) (2,20) (3,30) (4,1) (5,40) (6,56) ]

List , after deleting first record:

[ (5,40) (4,1) (3,30) (2,20) (1,10) ]

List , after deleting last record:

[ (5,40) (4,1) (3,30) (2,20) ]

List , insert after key(4) :

[ (5,40) (4,1) (7,13) (3,30) (2,20) ]

List , after delete key(4) :

[ (5,40) (4,13) (3,30) (2,20) ]

Key takeaway

Link − Each link of a linked list can store a data called an element.
Next − Each link of a linked list contains a link to the next link called Next.
Prev − Each link of a linked list contains a link to the previous link called Prev.
LinkedList − A Linked List contains the connection link to the first link called First and to the last link called Last.

Reference:

1 Data structure & algorithm analysis in C by Mark Allen Weiss published by Pearson Education (LPE)

2 Introduction to Data structure in C by A.N. Kathie published by Pearson Education (LPE)

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined