4.1 Introduction to stacks | unit 4 stacks queues

UNIT- 4

Stacks & Queues

4.1 Introduction to stacks

A Stack is a linear data structure that follows the LIFO (Last-In-First-Out) principle. Stack has one end, whereas the Queue has two ends (front and rear). It contains only one pointer top pointer pointing to the topmost element of the stack. Whenever an element is added in the stack, it is added on the top of the stack, and the element can be deleted only from the stack. In other words, a stack can be defined as a container in which insertion and deletion can be done from the one end known as the top of the stack.

Some key points related to stack

It is called as stack because it behaves like a real-world stack, piles of books, etc.
A Stack is an abstract data type with a pre-defined capacity, which means that it can store the elements of a limited size.
It is a data structure that follows some order to insert and delete the elements, and that order can be LIFO or FILO.

Working of Stack

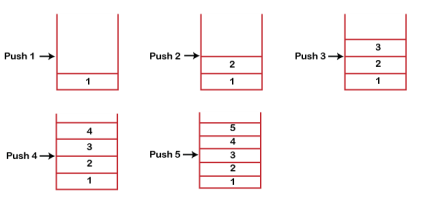
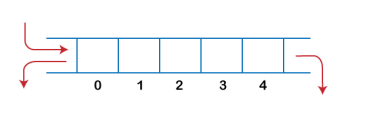
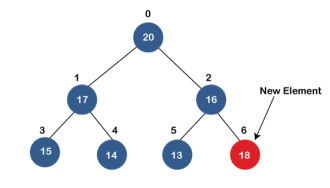
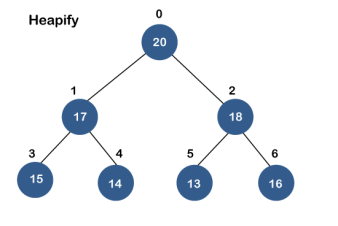
Stack works on the LIFO pattern. As we can observe in the below figure there are five memory blocks in the stack; therefore, the size of the stack is 5.

Suppose we want to store the elements in a stack and let's assume that stack is empty. We have taken the stack of size 5 as shown below in which we are pushing the elements one by one until the stack becomes full.

DS Stack Introduction

Fig 1 – Working of stack

Since our stack is full as the size of the stack is 5. In the above cases, we can observe that it goes from the top to the bottom when we were entering the new element in the stack. The stack gets filled up from the bottom to the top.

When we perform the delete operation on the stack, there is only one way for entry and exit as the other end is closed. It follows the LIFO pattern, which means that the value entered first will be removed last. In the above case, the value 5 is entered first, so it will be removed only after the deletion of all the other elements.

Standard Stack Operations

The following are some common operations implemented on the stack:

push(): When we insert an element in a stack then the operation is known as a push. If the stack is full then the overflow condition occurs.
pop(): When we delete an element from the stack, the operation is known as a pop. If the stack is empty means that no element exists in the stack, this state is known as an underflow state.
isEmpty(): It determines whether the stack is empty or not.
isFull(): It determines whether the stack is full or not.'
peek(): It returns the element at the given position.
count(): It returns the total number of elements available in a stack.
change(): It changes the element at the given position.
display(): It prints all the elements available in the stack.

PUSH operation

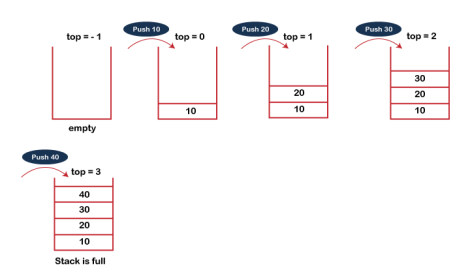
The steps involved in the PUSH operation is given below:

Before inserting an element in a stack, we check whether the stack is full.
If we try to insert the element in a stack, and the stack is full, then the overflow condition occurs.
When we initialize a stack, we set the value of top as -1 to check that the stack is empty.
When the new element is pushed in a stack, first, the value of the top gets incremented, i.e., top=top+1, and the element will be placed at the new position of the top.
The elements will be inserted until we reach the max size of the stack.

DS Stack Introduction

Fig 2 – Push Operation Example

POP operation

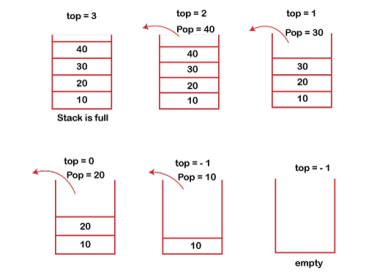
The steps involved in the POP operation is given below:

Before deleting the element from the stack, we check whether the stack is empty.
If we try to delete the element from the empty stack, then the underflow condition occurs.
If the stack is not empty, we first access the element which is pointed by the top
Once the pop operation is performed, the top is decremented by 1, i.e., top=top-1.

DS Stack Introduction

Fig 3 – Pop Operation example

Applications of Stack

The following are the applications of the stack:

Balancing of symbols: Stack is used for balancing a symbol. For example, we have the following program:

int main()
{
cout<<"Hello";
cout<<"javaTpoint";
}

As we know, each program has an opening and closing braces; when the opening braces come, we push the braces in a stack, and when the closing braces appear, we pop the opening braces from the stack. Therefore, the net value comes out to be zero. If any symbol is left in the stack, it means that some syntax occurs in a program.

String reversal: Stack is also used for reversing a string. For example, we want to reverse a "javaTpoint" string, so we can achieve this with the help of a stack.
First, we push all the characters of the string in a stack until we reach the null character.
After pushing all the characters, we start taking out the character one by one until we reach the bottom of the stack.
UNDO/REDO: It can also be used for performing UNDO/REDO operations. For example, we have an editor in which we write 'a', then 'b', and then 'c'; therefore, the text written in an editor is abc. So, there are three states, a, ab, and abc, which are stored in a stack. There would be two stacks in which one stack shows UNDO state, and the other shows REDO state.
If we want to perform UNDO operation, and want to achieve 'ab' state, then we implement pop operation.
Recursion: The recursion means that the function is calling itself again. To maintain the previous states, the compiler creates a system stack in which all the previous records of the function are maintained.
DFS(Depth First Search): This search is implemented on a Graph, and Graph uses the stack data structure.
Backtracking: Suppose we have to create a path to solve a maze problem. If we are moving in a particular path, and we realize that we come on the wrong way. In order to come at the beginning of the path to create a new path, we have to use the stack data structure.
Expression conversion: Stack can also be used for expression conversion. This is one of the most important applications of stack. The list of the expression conversion is given below:
Infix to prefix
Infix to postfix
Prefix to infix
Prefix to postfix

Postfix to infix

Memory management: The stack manages the memory. The memory is assigned in the contiguous memory blocks. The memory is known as stack memory as all the variables are assigned in a function call stack memory. The memory size assigned to the program is known to the compiler. When the function is created, all its variables are assigned in the stack memory. When the function completed its execution, all the variables assigned in the stack are released.

Key takeaway

4.2 Stack as an Abstract Data type

The abstract datatype is special kind of datatype, whose behavior is defined by a set of values and set of operations. The keyword “Abstract” is used as we can use these datatypes, we can perform different operations. But how those operations are working that is totally hidden from the user. The ADT is made of with primitive datatypes, but operation logics are hidden.

Here we will see the stack ADT. These are few operations or functions of the Stack ADT.

isFull(), This is used to check whether stack is full or not
isEmpry(), This is used to check whether stack is empty or not
push(x), This is used to push x into the stack
pop(), This is used to delete one element from top of the stack
peek(), This is used to get the top most element of the stack
size(), this function is used to get number of elements present into the stack

Example

#include<iostream>

#include<stack>

using namespace std;

main(){

stack<int> stk;

if(stk.empty()){

cout << "Stack is empty" << endl;

} else {

cout << "Stack is not empty" << endl;

}

//insert elements into stack

stk.push(10);

stk.push(20);

stk.push(30);

stk.push(40);

stk.push(50);

cout << "Size of the stack: " << stk.size() << endl;

//pop and dispay elements

while(!stk.empty()){

int item = stk.top(); // same as peek operation

stk.pop();

cout << item << " ";

}

Output

Stack is empty

Size of the stack: 5

50 40 30 20 10

Key takeaway

4.3 Representation through Arrays & linked lists

Array implementation of Stack

In array implementation, the stack is formed by using the array. All the operations regarding the stack are performed using arrays. Lets see how each operation can be implemented on the stack using array data structure.

Adding an element onto the stack (push operation)

Adding an element into the top of the stack is referred to as push operation. Push operation involves following two steps.

Increment the variable Top so that it can now refere to the next memory location.
Add element at the position of incremented top. This is referred to as adding new element at the top of the stack.

Stack is overflown when we try to insert an element into a completely filled stack therefore, our main function must always avoid stack overflow condition.

Algorithm:

begin
if top = n then stack full
top = top + 1
stack (top) : = item;
end

Time Complexity : o(1)

implementation of push algorithm in C language

void push (int val,int n) //n is size of the stack
{
if (top == n )
printf("\n Overflow");
else
{
top = top +1;
stack[top] = val;
}
}

Deletion of an element from a stack (Pop operation)

Deletion of an element from the top of the stack is called pop operation. The value of the variable top will be incremented by 1 whenever an item is deleted from the stack. The top most element of the stack is stored in an another variable and then the top is decremented by 1. the operation returns the deleted value that was stored in another variable as the result.

The underflow condition occurs when we try to delete an element from an already empty stack.

Algorithm :

begin
if top = 0 then stack empty;
item := stack(top);
top = top - 1;
end;

Time Complexity : o(1)

Implementation of POP algorithm using C language

int pop ()
{
if(top == -1)
{
printf("Underflow");
return 0;
}
else
{
return stack[top - - ];
}
}

Visiting each element of the stack (Peek operation)

Peek operation involves returning the element which is present at the top of the stack without deleting it. Underflow condition can occur if we try to return the top element in an already empty stack.

Algorithm :

PEEK (STACK, TOP)

Begin
if top = -1 then stack empty
item = stack[top]
return item
End

Time complexity: o(n)

Implementation of Peek algorithm in C language

int peek()
{
if (top == -1)
{
printf("Underflow");
return 0;
}
else
{
return stack [top];
}
}

C program

#include <stdio.h>
int stack[100],i,j,choice=0,n,top=-1;
void push();
void pop();
void show();
void main ()
{
printf("Enter the number of elements in the stack ");
scanf("%d",&n);
printf("*********Stack operations using array*********");
printf("\n----------------------------------------------\n");
while(choice != 4)
{
printf("Chose one from the below options...\n");
printf("\n1.Push\n2.Pop\n3.Show\n4.Exit");
printf("\n Enter your choice \n");
scanf("%d",&choice);
switch(choice)
{
case 1:
{
push();
break;
}
case 2:
{
pop();
break;
}
case 3:
{
show();
break;
}
case 4:
{
printf("Exiting....");
break;
}
default:
{
printf("Please Enter valid choice ");
}
};
}
}
void push ()
{
int val;
if (top == n )
printf("\n Overflow");
else
{
printf("Enter the value?");
scanf("%d",&val);
top = top +1;
stack[top] = val;
}
}
void pop ()
{
if(top == -1)
printf("Underflow");
else
top = top -1;
}
void show()
{
for (i=top;i>=0;i--)
{
printf("%d\n",stack[i]);
}
if(top == -1)
{
printf("Stack is empty");
}
}

Java Program

import java.util.Scanner;
class Stack
{
int top;
int maxsize = 10;
int[] arr = new int[maxsize];
boolean isEmpty()
{
return (top < 0);
}
Stack()
{
top = -1;
}
boolean push (Scanner sc)
{
if(top == maxsize-1)
{
System.out.println("Overflow !!");
return false;
}
else
{
System.out.println("Enter Value");
int val = sc.nextInt();
top++;
arr[top]=val;
System.out.println("Item pushed");
return true;
}
}
boolean pop ()
{
if (top == -1)
{
System.out.println("Underflow !!");
return false;
}
else
{
top --;
System.out.println("Item popped");
return true;
}
}
void display ()
{
System.out.println("Printing stack elements .....");
for(int i = top; i>=0;i--)
{
System.out.println(arr[i]);
}
}
}
public class Stack_Operations {
public static void main(String[] args) {
int choice=0;
Scanner sc = new Scanner(System.in);
Stack s = new Stack();
System.out.println("*********Stack operations using array*********\n");
System.out.println("\n------------------------------------------------\n");
while(choice != 4)
{
System.out.println("\nChose one from the below options...\n");
System.out.println("\n1.Push\n2.Pop\n3.Show\n4.Exit");
System.out.println("\n Enter your choice \n");
choice = sc.nextInt();
switch(choice)
{
case 1:
{
s.push(sc);
break;
}
case 2:
{
s.pop();
break;
}
case 3:
{
s.display();
break;
}
case 4:
{
System.out.println("Exiting....");
System.exit(0);
break;
}
default:
{
System.out.println("Please Enter valid choice ");
}
};
}
}
}

C# Program

using System;
public class Stack
{
int top;
int maxsize=10;
int[] arr = new int[10];
public static void Main()
{
Stack st = new Stack();
st.top=-1;
int choice=0;
Console.WriteLine("*********Stack operations using array*********");
Console.WriteLine("\n----------------------------------------------\n");
while(choice != 4)
{
Console.WriteLine("Chose one from the below options...\n");
Console.WriteLine("\n1.Push\n2.Pop\n3.Show\n4.Exit");
Console.WriteLine("\n Enter your choice \n");
choice = Convert.ToInt32(Console.ReadLine());
switch(choice)
{
case 1:
{
st.push();
break;
}
case 2:
{
st.pop();
break;
}
case 3:
{
st.show();
break;
}
case 4:
{
Console.WriteLine("Exiting....");
break;
}
default:
{
Console.WriteLine("Please Enter valid choice ");
break;
}
};
}
}
Boolean push ()
{
int val;
if(top == maxsize-1)
{
Console.WriteLine("\n Overflow");
return false;
}
else
{
Console.WriteLine("Enter the value?");
val = Convert.ToInt32(Console.ReadLine());
top = top +1;
arr[top] = val;
Console.WriteLine("Item pushed");
return true;
}
}
Boolean pop ()
{
if (top == -1)
{
Console.WriteLine("Underflow");
return false;
}
else
{
top = top -1;
Console.WriteLine("Item popped");
return true;
}
}
void show()
{
for (int i=top;i>=0;i--)
{
Console.WriteLine(arr[i]);
}
if(top == -1)
{
Console.WriteLine("Stack is empty");
}
}
}

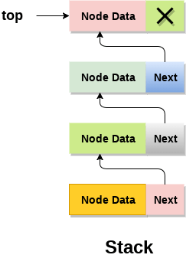
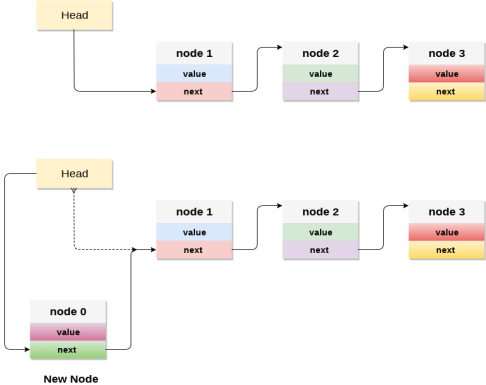
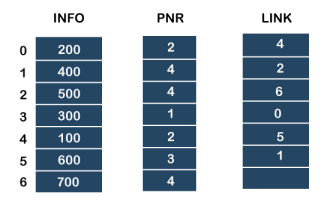
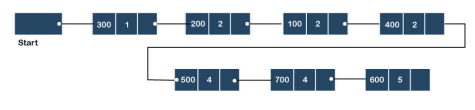
Linked list implementation of stack

Instead of using array, we can also use linked list to implement stack. Linked list allocates the memory dynamically. However, time complexity in both the scenario is same for all the operations i.e. push, pop and peek.

In linked list implementation of stack, the nodes are maintained non-contiguously in the memory. Each node contains a pointer to its immediate successor node in the stack. Stack is said to be overflown if the space left in the memory heap is not enough to create a node.

DS Linked list implementation stack

Fig 4 - Stack

The top most node in the stack always contains null in its address field. Lets discuss the way in which, each operation is performed in linked list implementation of stack.

Adding a node to the stack (Push operation)

Adding a node to the stack is referred to as push operation. Pushing an element to a stack in linked list implementation is different from that of an array implementation. In order to push an element onto the stack, the following steps are involved.

Create a node first and allocate memory to it.
If the list is empty then the item is to be pushed as the start node of the list. This includes assigning value to the data part of the node and assign null to the address part of the node.
If there are some nodes in the list already, then we have to add the new element in the beginning of the list (to not violate the property of the stack). For this purpose, assign the address of the starting element to the address field of the new node and make the new node, the starting node of the list.

Time Complexity : o(1)

DS Linked list implementation stack

Fig 5 – Time complexity

C implementation:

void push ()
{
int val;
struct node *ptr =(struct node*)malloc(sizeof(struct node));
if(ptr == NULL)
{
printf("not able to push the element");
}
else
{
printf("Enter the value");
scanf("%d",&val);
if(head==NULL)
{
ptr->val = val;
ptr -> next = NULL;
head=ptr;
}
else
{
ptr->val = val;
ptr->next = head;
head=ptr;
}
printf("Item pushed");
}
}

Deleting a node from the stack (POP operation)

Deleting a node from the top of stack is referred to as pop operation. Deleting a node from the linked list implementation of stack is different from that in the array implementation. In order to pop an element from the stack, we need to follow the following steps :

30. Check for the underflow condition: The underflow condition occurs when we try to pop from an already empty stack. The stack will be empty if the head pointer of the list points to null.

31. Adjust the head pointer accordingly: In stack, the elements are popped only from one end, therefore, the value stored in the head pointer must be deleted and the node must be freed. The next node of the head node now becomes the head node.

Time Complexity : o(n)

C implementation

32. void pop()

33. {

34. int item;

35. struct node *ptr;

36. if (head == NULL)

37. {

38. printf("Underflow");

39. }

40. else

41. {

42. item = head->val;

43. ptr = head;

44. head = head->next;

45. free(ptr);

46. printf("Item popped");

47.

48. }

49. }

Display the nodes (Traversing)

Displaying all the nodes of a stack needs traversing all the nodes of the linked list organized in the form of stack. For this purpose, we need to follow the following steps.

50. Copy the head pointer into a temporary pointer.

51. Move the temporary pointer through all the nodes of the list and print the value field attached to every node.

Time Complexity : o(n)

C Implementation

52. void display()

53. {

54. int i;

55. struct node *ptr;

56. ptr=head;

57. if(ptr == NULL)

58. {

59. printf("Stack is empty\n");

60. }

61. else

62. {

63. printf("Printing Stack elements \n");

64. while(ptr!=NULL)

65. {

66. printf("%d\n",ptr->val);

67. ptr = ptr->next;

68. }

69. }

70. }

Menu Driven program in C implementing all the stack operations using linked list :

71. #include <stdio.h>

72. #include <stdlib.h>

73. void push();

74. void pop();

75. void display();

76. struct node

77. {

78. int val;

79. struct node *next;

80. };

81. struct node *head;

82.

83. void main ()

84. {

85. int choice=0;

86. printf("\n*********Stack operations using linked list*********\n");

87. printf("\n----------------------------------------------\n");

88. while(choice != 4)

89. {

90. printf("\n\nChose one from the below options...\n");

91. printf("\n1.Push\n2.Pop\n3.Show\n4.Exit");

92. printf("\n Enter your choice \n");

93. scanf("%d",&choice);

94. switch(choice)

95. {

96. case 1:

97. {

98. push();

99. break;

100. }

101. case 2:

102. {

103. pop();

104. break;

105. }

106. case 3:

107. {

108. display();

109. break;

110. }

111. case 4:

112. {

113. printf("Exiting....");

114. break;

115. }

116. default:

117. {

118. printf("Please Enter valid choice ");

119. }

120. };

121. }

122. }

123. void push ()

124. {

125. int val;

126. struct node *ptr = (struct node*)malloc(sizeof(struct node));

127. if(ptr == NULL)

128. {

129. printf("not able to push the element");

130. }

131. else

132. {

133. printf("Enter the value");

134. scanf("%d",&val);

135. if(head==NULL)

136. {

137. ptr->val = val;

138. ptr -> next = NULL;

139. head=ptr;

140. }

141. else

142. {

143. ptr->val = val;

144. ptr->next = head;

145. head=ptr;

146.

147. }

148. printf("Item pushed");

149.

150. }

151. }

152.

153. void pop()

154. {

155. int item;

156. struct node *ptr;

157. if (head == NULL)

158. {

159. printf("Underflow");

160. }

161. else

162. {

163. item = head->val;

164. ptr = head;

165. head = head->next;

166. free(ptr);

167. printf("Item popped");

168.

169. }

170. }

171. void display()

172. {

173. int i;

174. struct node *ptr;

175. ptr=head;

176. if(ptr == NULL)

177. {

178. printf("Stack is empty\n");

179. }

180. else

181. {

182. printf("Printing Stack elements \n");

183. while(ptr!=NULL)

184. {

185. printf("%d\n",ptr->val);

186. ptr = ptr->next;

187. }

188. }

189. }

Key takeaway

4.4 Arithmetic expressions, Polish notation

The way to write arithmetic expression is known as a notation. An arithmetic expression can be written in three different but equivalent notations, i.e., without changing the essence or output of an expression. These notations are −

Infix Notation
Prefix (Polish) Notation
Postfix (Reverse-Polish) Notation

These notations are named as how they use operator in expression. We shall learn the same here in this chapter.

Infix Notation

We write expression in infix notation, e.g. a - b + c, where operators are used in-between operands. It is easy for us humans to read, write, and speak in infix notation but the same does not go well with computing devices. An algorithm to process infix notation could be difficult and costly in terms of time and space consumption.

Prefix Notation

In this notation, operator is prefixed to operands, i.e. operator is written ahead of operands. For example, +ab. This is equivalent to its infix notation a + b. Prefix notation is also known as Polish Notation.

Postfix Notation

This notation style is known as Reversed Polish Notation. In this notation style, the operator is postfixed to the operands i.e., the operator is written after the operands. For example, ab+. This is equivalent to its infix notation a + b.

The following table briefly tries to show the difference in all three notations −

Sr.No.	Infix Notation	Prefix Notation	Postfix Notation
1	a + b	+ a b	a b +
2	(a + b) ∗ c	∗ + a b c	a b + c ∗
3	a ∗ (b + c)	∗ a + b c	a b c + ∗
4	a / b + c / d	+ / a b / c d	a b / c d / +
5	(a + b) ∗ (c + d)	∗ + a b + c d	a b + c d + ∗
6	((a + b) ∗ c) - d	- ∗ + a b c d	a b + c ∗ d -

Parsing Expressions

As we have discussed, it is not a very efficient way to design an algorithm or program to parse infix notations. Instead, these infix notations are first converted into either postfix or prefix notations and then computed.

To parse any arithmetic expression, we need to take care of operator precedence and associativity also.

Precedence

When an operand is in between two different operators, which operator will take the operand first, is decided by the precedence of an operator over others. For example −

Operator Precendence

As multiplication operation has precedence over addition, b * c will be evaluated first. A table of operator precedence is provided later.

Associativity

Associativity describes the rule where operators with the same precedence appear in an expression. For example, in expression a + b − c, both + and – have the same precedence, then which part of the expression will be evaluated first, is determined by associativity of those operators. Here, both + and − are left associative, so the expression will be evaluated as (a + b) − c.

Precedence and associativity determines the order of evaluation of an expression. Following is an operator precedence and associativity table (highest to lowest) −

Sr.No.	Operator	Precedence	Associativity
1	Exponentiation ^	Highest	Right Associative
2	Multiplication ( ∗ ) & Division ( / )	Second Highest	Left Associative
3	Addition ( + ) & Subtraction ( − )	Lowest	Left Associative

The above table shows the default behavior of operators. At any point of time in expression evaluation, the order can be altered by using parenthesis. For example −

In a + b*c, the expression part b*c will be evaluated first, with multiplication as precedence over addition. We here use parenthesis for a + b to be evaluated first, like (a + b)*c.

Postfix Evaluation Algorithm

We shall now look at the algorithm on how to evaluate postfix notation −

Step 1 − scan the expression from left to right

Step 2 − if it is an operand push it to stack

Step 3 − if it is an operator pull operand from stack and perform operation

Step 4 − store the output of step 3, back to stack

Step 5 − scan the expression until all operands are consumed

Step 6 − pop the stack and perform operation

Infix notation is easier for humans to read and understand whereas for electronic machines like computers, postfix is the best form of expression to parse. We shall see here a program to convert and evaluate infix notation to postfix notation −

Example

#include<stdio.h>

#include<string.h>

//char stack

char stack[25];

int top = -1;

void push(char item) {

stack[++top] = item;

}

char pop() {

return stack[top--];

}

//returns precedence of operators

int precedence(char symbol) {

switch(symbol) {

case '+':

case '-':

return 2;

break;

case '*':

case '/':

return 3;

break;

case '^':

return 4;

break;

case '(':

case ')':

case '#':

return 1;

break;

}

//check whether the symbol is operator?

int isOperator(char symbol) {

switch(symbol) {

case '+':

case '-':

case '*':

case '/':

case '^':

case '(':

case ')':

return 1;

break;

default:

return 0;

}

//converts infix expression to postfix

void convert(char infix[],char postfix[]) {

int i,symbol,j = 0;

stack[++top] = '#';

for(i = 0;i<strlen(infix);i++) {

symbol = infix[i];

if(isOperator(symbol) == 0) {

postfix[j] = symbol;

j++;

} else {

if(symbol == '(') {

push(symbol);

} else {

if(symbol == ')') {

while(stack[top] != '(') {

postfix[j] = pop();

j++;

}

pop(); //pop out (.

} else {

if(precedence(symbol)>precedence(stack[top])) {

push(symbol);

} else {

while(precedence(symbol)<=precedence(stack[top])) {

postfix[j] = pop();

j++;

}

push(symbol);

}

while(stack[top] != '#') {

postfix[j] = pop();

j++;

}

postfix[j]='\0'; //null terminate string.

}

//int stack

int stack_int[25];

int top_int = -1;

void push_int(int item) {

stack_int[++top_int] = item;

}

char pop_int() {

return stack_int[top_int--];

}

//evaluates postfix expression

int evaluate(char *postfix){

char ch;

int i = 0,operand1,operand2;

while( (ch = postfix[i++]) != '\0') {

if(isdigit(ch)) {

push_int(ch-'0'); // Push the operand

} else {

//Operator,pop two operands

operand2 = pop_int();

operand1 = pop_int();

switch(ch) {

case '+':

push_int(operand1+operand2);

break;

case '-':

push_int(operand1-operand2);

break;

case '*':

push_int(operand1*operand2);

break;

case '/':

push_int(operand1/operand2);

break;

}

return stack_int[top_int];

}

void main() {

char infix[25] = "1*(2+3)",postfix[25];

convert(infix,postfix);

printf("Infix expression is: %s\n" , infix);

printf("Postfix expression is: %s\n" , postfix);

printf("Evaluated expression is: %d\n" , evaluate(postfix));

}

If we compile and run the above program, it will produce the following result −

Output

Infix expression is: 1*(2+3)

Postfix expression is: 123+*

Result is: 5

Key takeaway

Infix Notation
Prefix (Polish) Notation
Postfix (Reverse-Polish) Notation

4.5 Applications of stacks

The Stack is Last In First Out (LIFO) data structure. This data structure has some important applications in different aspect. These are like below −

Expression Handling −
- Infix to Postfix or Infix to Prefix Conversion −

The stack can be used to convert some infix expression into its postfix equivalent, or prefix equivalent. These postfix or prefix notations are used in computers to express some expressions. These expressions are not so much familiar to the infix expression, but they have some great advantages also. We do not need to maintain operator ordering, and parenthesis.

Postfix or Prefix Evaluation −

After converting into prefix or postfix notations, we have to evaluate the expression to get the result. For that purpose, also we need the help of stack data structure.

Backtracking Procedure −

Backtracking is one of the algorithm designing technique. For that purpose, we dive into some way, if that way is not efficient, we come back to the previous state and go into some other paths. To get back from current state, we need to store the previous state. For that purpose, we need stack. Some examples of backtracking is finding the solution for Knight Tour problem or N-Queen Problem etc.

Another great use of stack is during the function call and return process. When we call a function from one other function, that function call statement may not be the first statement. After calling the function, we also have to come back from the function area to the place, where we have left our control. So we want to resume our task, not restart. For that reason, we store the address of the program counter into the stack, then go to the function body to execute it. After completion of the execution, it pops out the address from stack and assign it into the program counter to resume the task again.

Key takeaway

4.6 Stacks & Recursion

Some computer programming languages allow a module or function to call itself. This technique is known as recursion. In recursion, a function α either calls itself directly or calls a function β that in turn calls the original function α. The function α is called recursive function.

Example − a function calling itself.

int function(int value) {

if(value < 1)

return;

function(value - 1);

printf("%d ",value);

}

Example − a function that calls another function which in turn calls it again.

int function1(int value1) {

if(value1 < 1)

return;

function2(value1 - 1);

printf("%d ",value1);

}

int function2(int value2) {

function1(value2);

}

Properties

A recursive function can go infinite like a loop. To avoid infinite running of recursive function, there are two properties that a recursive function must have −

Base criteria − There must be at least one base criteria or condition, such that, when this condition is met the function stops calling itself recursively.
Progressive approach − The recursive calls should progress in such a way that each time a recursive call is made it comes closer to the base criteria.

Implementation

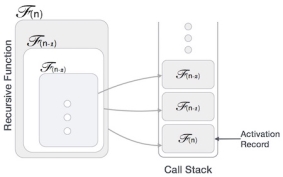
Many programming languages implement recursion by means of stacks. Generally, whenever a function (caller) calls another function (callee) or itself as callee, the caller function transfers execution control to the callee. This transfer process may also involve some data to be passed from the caller to the callee.

This implies, the caller function has to suspend its execution temporarily and resume later when the execution control returns from the callee function. Here, the caller function needs to start exactly from the point of execution where it puts itself on hold. It also needs the exact same data values it was working on. For this purpose, an activation record (or stack frame) is created for the caller function.

Activation Records

Fig 6 – Call stack

This activation record keeps the information about local variables, formal parameters, return address and all information passed to the caller function.

Analysis of Recursion

One may argue why to use recursion, as the same task can be done with iteration. The first reason is, recursion makes a program more readable and because of latest enhanced CPU systems, recursion is more efficient than iterations.

Time Complexity

In case of iterations, we take number of iterations to count the time complexity. Likewise, in case of recursion, assuming everything is constant, we try to figure out the number of times a recursive call is being made. A call made to a function is Ο(1), hence the (n) number of times a recursive call is made makes the recursive function Ο(n).

Space Complexity

Space complexity is counted as what amount of extra space is required for a module to execute. In case of iterations, the compiler hardly requires any extra space. The compiler keeps updating the values of variables used in the iterations. But in case of recursion, the system needs to store activation record each time a recursive call is made. Hence, it is considered that space complexity of recursive function may go higher than that of a function with iteration.

Key takeaway

4.7 Queue

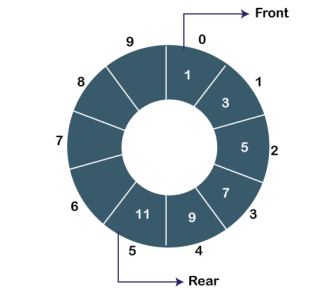
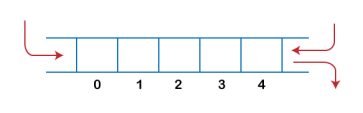
1. A queue can be defined as an ordered list which enables insert operations to be performed at one end called REAR and delete operations to be performed at another end called FRONT.

2. Queue is referred to be as First In First Out list.

3. For example, people waiting in line for a rail ticket form a queue.

ds Queue

Fig 7 - Queue

Applications of Queue

Due to the fact that queue performs actions on first in first out basis which is quite fair for the ordering of actions. There are various applications of queues discussed as below.

Queues are widely used as waiting lists for a single shared resource like printer, disk, CPU.
Queues are used in asynchronous transfer of data (where data is not being transferred at the same rate between two processes) for eg. pipes, file IO, sockets.
Queues are used as buffers in most of the applications like MP3 media player, CD player, etc.
Queue are used to maintain the play list in media players in order to add and remove the songs from the play-list.
Queues are used in operating systems for handling interrupts.

Complexity

Data Structure	Time Complexity								Space Compleity
	Average				Worst				Worst
	Access	Search	Insertion	Deletion	Access	Search	Insertion	Deletion
Queue	θ(n)	θ(n)	θ(1)	θ(1)	O(n)	O(n)	O(1)	O(1)	O(n)

Types of Queues

Before understanding the types of queues, we first look at 'what is Queue'.

What is the Queue?

A queue in the data structure can be considered similar to the queue in the real-world. A queue is a data structure in which whatever comes first will go out first. It follows the FIFO (First-In-First-Out) policy. In Queue, the insertion is done from one end known as the rear end or the tail of the queue, whereas the deletion is done from another end known as the front end or the head of the queue. In other words, it can be defined as a list or a collection with a constraint that the insertion can be performed at one end called as the rear end or tail of the queue and deletion is performed on another end called as the front end or the head of the queue.

Types of Queues

Fig 8 - Dequeue

Operations on Queue

There are two fundamental operations performed on a Queue:

Enqueue: The enqueue operation is used to insert the element at the rear end of the queue. It returns void.
Dequeue: The dequeue operation performs the deletion from the front-end of the queue. It also returns the element which has been removed from the front-end. It returns an integer value. The dequeue operation can also be designed to void.
Peek: This is the third operation that returns the element, which is pointed by the front pointer in the queue but does not delete it.
Queue overflow (isfull): When the Queue is completely full, then it shows the overflow condition.
Queue underflow (isempty): When the Queue is empty, i.e., no elements are in the Queue then it throws the underflow condition.

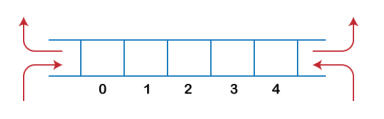
A Queue can be represented as a container opened from both the sides in which the element can be enqueued from one side and dequeued from another side as shown in the below figure:

Implementation of Queue

There are two ways of implementing the Queue:

Sequential allocation: The sequential allocation in a Queue can be implemented using an array.

Linked list allocation: The linked list allocation in a Queue can be implemented using a linked list.

What are the use cases of Queue?

Here, we will see the real-world scenarios where we can use the Queue data structure. The Queue data structure is mainly used where there is a shared resource that has to serve the multiple requests but can serve a single request at a time. In such cases, we need to use the Queue data structure for queuing up the requests. The request that arrives first in the queue will be served first. The following are the real-world scenarios in which the Queue concept is used:

Suppose we have a printer shared between various machines in a network, and any machine or computer in a network can send a print request to the printer. But, the printer can serve a single request at a time, i.e., a printer can print a single document at a time. When any print request comes from the network, and if the printer is busy, the printer's program will put the print request in a queue.
. If the requests are available in the Queue, the printer takes a request from the front of the queue, and serves it.
The processor in a computer is also used as a shared resource. There are multiple requests that the processor must execute, but the processor can serve a single request or execute a single process at a time. Therefore, the processes are kept in a Queue for execution.

Types of Queue

There are four types of Queues:

Linear Queue

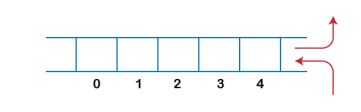
In Linear Queue, an insertion takes place from one end while the deletion occurs from another end. The end at which the insertion takes place is known as the rear end, and the end at which the deletion takes place is known as front end. It strictly follows the FIFO rule. The linear Queue can be represented, as shown in the below figure:

Types of Queues

Fig 9 – Linear queue

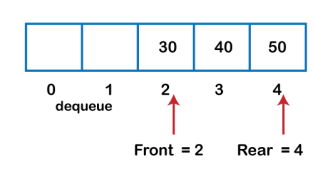
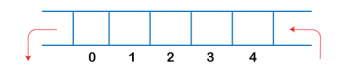
The above figure shows that the elements are inserted from the rear end, and if we insert more elements in a Queue, then the rear value gets incremented on every insertion. If we want to show the deletion, then it can be represented as:

Types of Queues

Fig 10 - Example

In the above figure, we can observe that the front pointer points to the next element, and the element which was previously pointed by the front pointer was deleted.

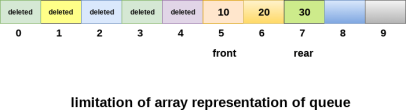
The major drawback of using a linear Queue is that insertion is done only from the rear end. If the first three elements are deleted from the Queue, we cannot insert more elements even though the space is available in a Linear Queue. In this case, the linear Queue shows the overflow condition as the rear is pointing to the last element of the Queue.

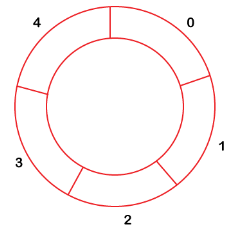
Circular Queue

In Circular Queue, all the nodes are represented as circular. It is similar to the linear Queue except that the last element of the queue is connected to the first element. It is also known as Ring Buffer as all the ends are connected to another end. The circular queue can be represented as:

Types of Queues

Fig 11 – Circular queue

The drawback that occurs in a linear queue is overcome by using the circular queue. If the empty space is available in a circular queue, the new element can be added in an empty space by simply incrementing the value of rear.

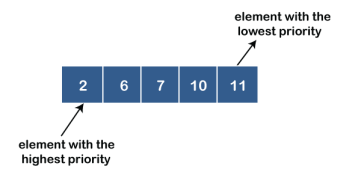
Priority Queue

A priority queue is another special type of Queue data structure in which each element has some priority associated with it. Based on the priority of the element, the elements are arranged in a priority queue. If the elements occur with the same priority, then they are served according to the FIFO principle.

In priority Queue, the insertion takes place based on the arrival while the deletion occurs based on the priority. The priority Queue can be shown as:

The above figure shows that the highest priority element comes first and the elements of the same priority are arranged based on FIFO structure.

Deque

Both the Linear Queue and Deque are different as the linear queue follows the FIFO principle whereas, deque does not follow the FIFO principle. In Deque, the insertion and deletion can occur from both ends.

Key takeaway

1. A queue can be defined as an ordered list which enables insert operations to be performed at one end called REAR and delete operations to be performed at another end called FRONT.

2. Queue is referred to be as First In First Out list.

3. For example, people waiting in line for a rail ticket form a queue.

4.8 Representation of queue as an array and as a linked list

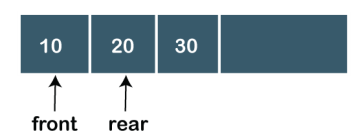
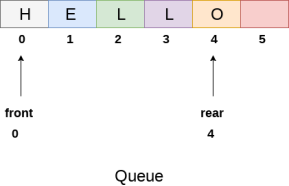
Array representation of Queue

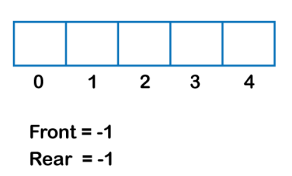
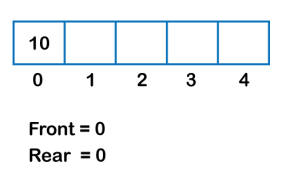
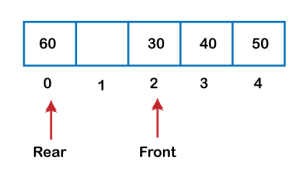
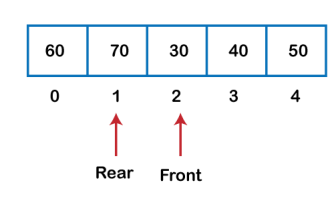
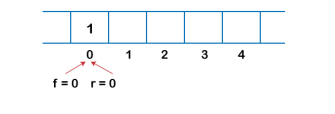
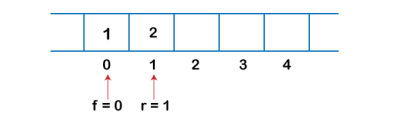
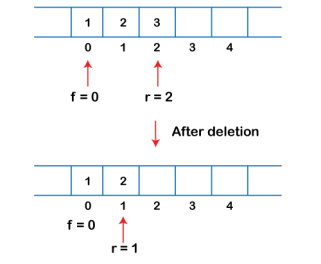
We can easily represent queue by using linear arrays. There are two variables i.e. front and rear, that are implemented in the case of every queue. Front and rear variables point to the position from where insertions and deletions are performed in a queue. Initially, the value of front and queue is -1 which represents an empty queue. Array representation of a queue containing 5 elements along with the respective values of front and rear, is shown in the following figure.

Array representation of Queue

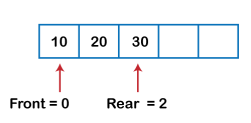
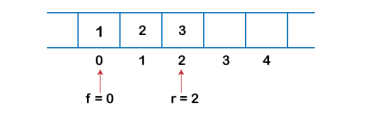
Fig 12 – Queue Example

The above figure shows the queue of characters forming the English word "HELLO". Since, No deletion is performed in the queue till now, therefore the value of front remains -1 . However, the value of rear increases by one every time an insertion is performed in the queue. After inserting an element into the queue shown in the above figure, the queue will look something like following. The value of rear will become 5 while the value of front remains same.

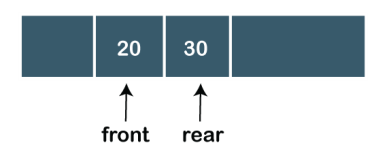
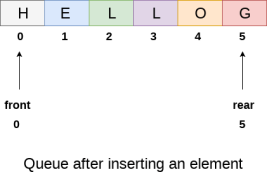
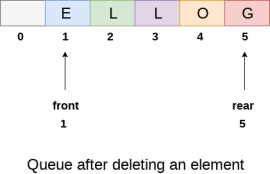
Array representation of Queue

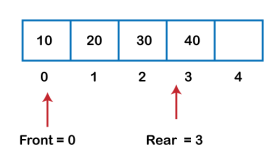
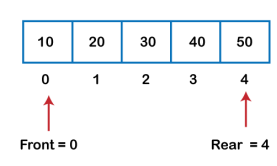
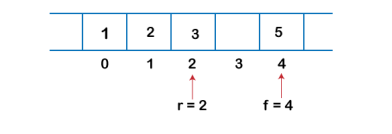
Fig 13 – Insertion Example

After deleting an element, the value of front will increase from -1 to 0. however, the queue will look something like following.

Array representation of Queue

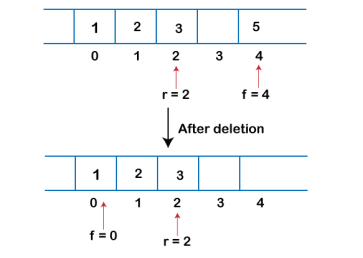
Fig 14 – Deletion Example

Algorithm to insert any element in a queue

Check if the queue is already full by comparing rear to max - 1. if so, then return an overflow error.

If the item is to be inserted as the first element in the list, in that case set the value of front and rear to 0 and insert the element at the rear end.

Otherwise keep increasing the value of rear and insert each element one by one having rear as the index.

Algorithm

Step 1: IF REAR = MAX - 1
Write OVERFLOW
Go to step
[END OF IF]
Step 2: IF FRONT = -1 and REAR = -1
SET FRONT = REAR = 0
ELSE
SET REAR = REAR + 1
[END OF IF]
Step 3: Set QUEUE[REAR] = NUM
Step 4: EXIT

C Function

void insert (int queue[], int max, int front, int rear, int item)
{
if (rear + 1 == max)
{
printf("overflow");
}
else
{
if(front == -1 && rear == -1)
{
front = 0;
rear = 0;
}
else
{
rear = rear + 1;
}
queue[rear]=item;
}
}

Algorithm to delete an element from the queue

If, the value of front is -1 or value of front is greater than rear , write an underflow message and exit.

Otherwise, keep increasing the value of front and return the item stored at the front end of the queue at each time.

Algorithm

Step 1: IF FRONT = -1 or FRONT > REAR
Write UNDERFLOW
ELSE
SET VAL = QUEUE[FRONT]
SET FRONT = FRONT + 1
[END OF IF]
Step 2: EXIT

C Function

int delete (int queue[], int max, int front, int rear)
{
int y;
if (front == -1 || front > rear)
{
printf("underflow");
}
else
{
y = queue[front];
if(front == rear)
{
front = rear = -1;
else
front = front + 1;
}
return y;
}
}

Menu driven program to implement queue using array

#include<stdio.h>
#include<stdlib.h>
#define maxsize 5
void insert();
void delete();
void display();
int front = -1, rear = -1;
int queue[maxsize];
void main ()
{
int choice;
while(choice != 4)
{
printf("\n*************************Main Menu*****************************\n");
printf("\n=================================================================\n");
printf("\n1.insert an element\n2.Delete an element\n3.Display the queue\n4.Exit\n");
printf("\nEnter your choice ?");
scanf("%d",&choice);
switch(choice)
{
case 1:
insert();
break;
case 2:
delete();
break;
case 3:
display();
break;
case 4:
exit(0);
break;
default:
printf("\nEnter valid choice??\n");
}
}
}
void insert()
{
int item;
printf("\nEnter the element\n");
scanf("\n%d",&item);
if(rear == maxsize-1)
{
printf("\nOVERFLOW\n");
return;
}
if(front == -1 && rear == -1)
{
front = 0;
rear = 0;
}
else
{
rear = rear+1;
}
queue[rear] = item;
printf("\nValue inserted ");
}
void delete()
{
int item;
if (front == -1 || front > rear)
{
printf("\nUNDERFLOW\n");
return;
}
else
{
item = queue[front];
if(front == rear)
{
front = -1;
rear = -1 ;
}
else
{
front = front + 1;
}
printf("\nvalue deleted ");
}
}
void display()
{
int i;
if(rear == -1)
{
printf("\nEmpty queue\n");
}
else
{ printf("\nprinting values .....\n");
for(i=front;i<=rear;i++)
{
printf("\n%d\n",queue[i]);
}
}
}

Output:

*************Main Menu**************

==============================================

1.insert an element

2.Delete an element

3.Display the queue

4.Exit

Enter your choice ?1

Enter the element

123

Value inserted

*************Main Menu**************

==============================================

1.insert an element

2.Delete an element

3.Display the queue

4.Exit

Enter your choice ?1

Enter the element

Value inserted

*************Main Menu**************

===================================

1.insert an element

2.Delete an element

3.Display the queue

4.Exit

Enter your choice ?2

value deleted

*************Main Menu**************

==============================================

1.insert an element

2.Delete an element

3.Display the queue

4.Exit

Enter your choice ?3

printing values .....

*************Main Menu**************

==============================================

1.insert an element

2.Delete an element

3.Display the queue

4.Exit

Enter your choice ?4

Drawback of array implementation

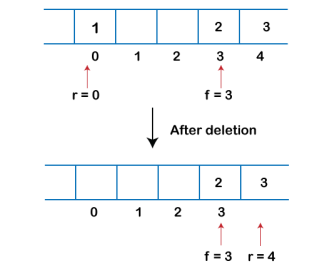
Although, the technique of creating a queue is easy, but there are some drawbacks of using this technique to implement a queue.

Memory wastage : The space of the array, which is used to store queue elements, can never be reused to store the elements of that queue because the elements can only be inserted at front end and the value of front might be so high so that, all the space before that, can never be filled.

Array representation of Queue

Fig 15 – Array representation of queue

The above figure shows how the memory space is wasted in the array representation of queue. In the above figure, a queue of size 10 having 3 elements, is shown. The value of the front variable is 5, therefore, we can not reinsert the values in the place of already deleted element before the position of front. That much space of the array is wasted and can not be used in the future (for this queue).

Deciding the array size

On of the most common problem with array implementation is the size of the array which requires to be declared in advance. Due to the fact that, the queue can be extended at runtime depending upon the problem, the extension in the array size is a time taking process and almost impossible to be performed at runtime since a lot of reallocations take place. Due to this reason, we can declare the array large enough so that we can store queue elements as enough as possible but the main problem with this declaration is that, most of the array slots (nearly half) can never be reused. It will again lead to memory wastage.

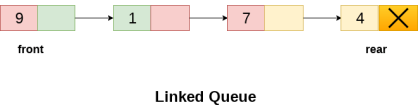
Linked List implementation of Queue

Due to the drawbacks discussed in the previous section of this tutorial, the array implementation can not be used for the large scale applications where the queues are implemented. One of the alternative of array implementation is linked list implementation of queue.

The storage requirement of linked representation of a queue with n elements is o(n) while the time requirement for operations is o(1).

In a linked queue, each node of the queue consists of two parts i.e. data part and the link part. Each element of the queue points to its immediate next element in the memory.

In the linked queue, there are two pointers maintained in the memory i.e. front pointer and rear pointer. The front pointer contains the address of the starting element of the queue while the rear pointer contains the address of the last element of the queue.

Insertion and deletions are performed at rear and front end respectively. If front and rear both are NULL, it indicates that the queue is empty.

The linked representation of queue is shown in the following figure.

Linked List implementation of Queue

Fig 16 – Linked queue

Operation on Linked Queue

There are two basic operations which can be implemented on the linked queues. The operations are Insertion and Deletion.

Insert operation

The insert operation append the queue by adding an element to the end of the queue. The new element will be the last element of the queue.

Firstly, allocate the memory for the new node ptr by using the following statement.

Ptr = (struct node *) malloc (sizeof(struct node));

There can be the two scenario of inserting this new node ptr into the linked queue.

In the first scenario, we insert element into an empty queue. In this case, the condition front = NULL becomes true. Now, the new element will be added as the only element of the queue and the next pointer of front and rear pointer both, will point to NULL.

ptr -> data = item;
if(front == NULL)
{
front = ptr;
rear = ptr;
front -> next = NULL;
rear -> next = NULL;
}

In the second case, the queue contains more than one element. The condition front = NULL becomes false. In this scenario, we need to update the end pointer rear so that the next pointer of rear will point to the new node ptr. Since, this is a linked queue, hence we also need to make the rear pointer point to the newly added node ptr. We also need to make the next pointer of rear point to NULL.

rear -> next = ptr;
rear = ptr;
rear->next = NULL;

In this way, the element is inserted into the queue. The algorithm and the C implementation is given as follows.

Algorithm

Step 1: Allocate the space for the new node PTR
Step 2: SET PTR -> DATA = VAL
Step 3: IF FRONT = NULL
SET FRONT = REAR = PTR
SET FRONT -> NEXT = REAR -> NEXT = NULL
ELSE
SET REAR -> NEXT = PTR
SET REAR = PTR
SET REAR -> NEXT = NULL
[END OF IF]
Step 4: END

C Function

void insert(struct node *ptr, int item; )
{
ptr = (struct node *) malloc (sizeof(struct node));
if(ptr == NULL)
{
printf("\nOVERFLOW\n");
return;
}
else
{
ptr -> data = item;
if(front == NULL)
{
front = ptr;
rear = ptr;
front -> next = NULL;
rear -> next = NULL;
}
else
{
rear -> next = ptr;
rear = ptr;
rear->next = NULL;
}
}
}

Deletion

Deletion operation removes the element that is first inserted among all the queue elements. Firstly, we need to check either the list is empty or not. The condition front == NULL becomes true if the list is empty, in this case , we simply write underflow on the console and make exit.

Otherwise, we will delete the element that is pointed by the pointer front. For this purpose, copy the node pointed by the front pointer into the pointer ptr. Now, shift the front pointer, point to its next node and free the node pointed by the node ptr. This is done by using the following statements.

ptr = front;
front = front -> next;
free(ptr);

The algorithm and C function is given as follows.

Algorithm

Step 1: IF FRONT = NULL
Write " Underflow "
Go to Step 5
[END OF IF]
Step 2: SET PTR = FRONT
Step 3: SET FRONT = FRONT -> NEXT
Step 4: FREE PTR
Step 5: END

C Function

void delete (struct node *ptr)
{
if(front == NULL)
{
printf("\nUNDERFLOW\n");
return;
}
else
{
ptr = front;
front = front -> next;
free(ptr);
}
}

Menu-Driven Program implementing all the operations on Linked Queue

#include<stdio.h>
#include<stdlib.h>
struct node
{
int data;
struct node *next;
};
struct node *front;
struct node *rear;
void insert();
void delete();
void display();
void main ()
{
int choice;
while(choice != 4)
{
printf("\n*************************Main Menu*****************************\n");
printf("\n=================================================================\n");
printf("\n1.insert an element\n2.Delete an element\n3.Display the queue\n4.Exit\n");
printf("\nEnter your choice ?");
scanf("%d",& choice);
switch(choice)
{
case 1:
insert();
break;
case 2:
delete();
break;
case 3:
display();
break;
case 4:
exit(0);
break;
default:
printf("\nEnter valid choice??\n");
}
}
}
void insert()
{
struct node *ptr;
int item;
ptr = (struct node *) malloc (sizeof(struct node));
if(ptr == NULL)
{
printf("\nOVERFLOW\n");
return;
}
else
{
printf("\nEnter value?\n");
scanf("%d",&item);
ptr -> data = item;
if(front == NULL)
{
front = ptr;
rear = ptr;
front -> next = NULL;
rear -> next = NULL;
}
else
{
rear -> next = ptr;
rear = ptr;
rear->next = NULL;
}
}
}
void delete ()
{
struct node *ptr;
if(front == NULL)
{
printf("\nUNDERFLOW\n");
return;
}
else
{
ptr = front;
front = front -> next;
free(ptr);
}
}
void display()
{
struct node *ptr;
ptr = front;
if(front == NULL)
{
printf("\nEmpty queue\n");
}
else
{ printf("\nprinting values .....\n");
while(ptr != NULL)
{
printf("\n%d\n",ptr -> data);
ptr = ptr -> next;
}
}
}

Output:

***********Main Menu**********

==============================

1.insert an element

2.Delete an element

3.Display the queue

4.Exit

Enter your choice ?1

Enter value?

123

***********Main Menu**********

==============================

1.insert an element

2.Delete an element

3.Display the queue

4.Exit

Enter your choice ?1

Enter value?

***********Main Menu**********

==============================

1.insert an element

2.Delete an element

3.Display the queue

4.Exit

Enter your choice ?3

printing values .....

123

***********Main Menu**********

==============================

1.insert an element

2.Delete an element

3.Display the queue

4.Exit

Enter your choice ?2

***********Main Menu**********

==============================

1.insert an element

2.Delete an element

3.Display the queue

4.Exit

Enter your choice ?3

printing values .....

***********Main Menu**********

==============================

1.insert an element

2.Delete an element

3.Display the queue

4.Exit

Enter your choice ?4

Key takeaway

4.9 Circular, double ended, priority, application of queues

Circular Queue

Why was the concept of the circular queue introduced?

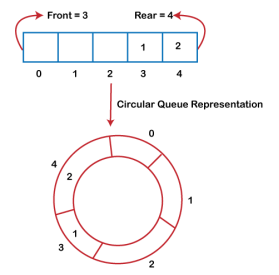
There was one limitation in the array implementation of Queue. If the rear reaches to the end position of the Queue then there might be possibility that some vacant spaces are left in the beginning which cannot be utilized. So, to overcome such limitations, the concept of the circular queue was introduced.

Circular Queue

Fig 17 – Circular queue

As we can see in the above image, the rear is at the last position of the Queue and front is pointing somewhere rather than the 0th position. In the above array, there are only two elements and other three positions are empty. The rear is at the last position of the Queue; if we try to insert the element then it will show that there are no empty spaces in the Queue. There is one solution to avoid such wastage of memory space by shifting both the elements at the left and adjust the front and rear end accordingly. It is not a practically good approach because shifting all the elements will consume lots of time. The efficient approach to avoid the wastage of the memory is to use the circular queue data structure.

What is a Circular Queue?

A circular queue is similar to a linear queue as it is also based on the FIFO (First In First Out) principle except that the last position is connected to the first position in a circular queue that forms a circle. It is also known as a Ring Buffer.

Operations on Circular Queue

The following are the operations that can be performed on a circular queue:

Front: It is used to get the front element from the Queue.
Rear: It is used to get the rear element from the Queue.
enQueue(value): This function is used to insert the new value in the Queue. The new element is always inserted from the rear end.
deQueue(): This function deletes an element from the Queue. The deletion in a Queue always takes place from the front end.

Applications of Circular Queue

The circular Queue can be used in the following scenarios:

Memory management: The circular queue provides memory management. As we have already seen that in linear queue, the memory is not managed very efficiently. But in case of a circular queue, the memory is managed efficiently by placing the elements in a location which is unused.
CPU Scheduling: The operating system also uses the circular queue to insert the processes and then execute them.
Traffic system: In a computer-control traffic system, traffic light is one of the best examples of the circular queue. Each light of traffic light gets ON one by one after every jinterval of time. Like red light gets ON for one minute then yellow light for one minute and then green light. After green light, the red light gets ON.

Enqueue operation

The steps of enqueue operation are given below:

First, we will check whether the Queue is full or not.
Initially the front and rear are set to -1. When we insert the first element in a Queue, front and rear both are set to 0.
When we insert a new element, the rear gets incremented, i.e., rear=rear+1.

Scenarios for inserting an element

There are two scenarios in which queue is not full:

If rear != max - 1, then rear will be incremented to mod(maxsize) and the new value will be inserted at the rear end of the queue.
If front != 0 and rear = max - 1, it means that queue is not full, then set the value of rear to 0 and insert the new element there.

There are two cases in which the element cannot be inserted:

When front ==0 && rear = max-1, which means that front is at the first position of the Queue and rear is at the last position of the Queue.
front== rear + 1;

Algorithm to insert an element in a circular queue

Step 1: IF (REAR+1)%MAX = FRONT
Write " OVERFLOW "
Goto step 4
[End OF IF]

Step 2: IF FRONT = -1 and REAR = -1
SET FRONT = REAR = 0
ELSE IF REAR = MAX - 1 and FRONT ! = 0
SET REAR = 0
ELSE
SET REAR = (REAR + 1) % MAX
[END OF IF]

Step 3: SET QUEUE[REAR] = VAL

Step 4: EXIT

Dequeue Operation

The steps of dequeue operation are given below:

First, we check whether the Queue is empty or not. If the queue is empty, we cannot perform the dequeue operation.
When the element is deleted, the value of front gets decremented by 1.
If there is only one element left which is to be deleted, then the front and rear are reset to -1.

Algorithm to delete an element from the circular queue

Step 1: IF FRONT = -1
Write " UNDERFLOW "
Goto Step 4
[END of IF]

Step 2: SET VAL = QUEUE[FRONT]

Step 3: IF FRONT = REAR
SET FRONT = REAR = -1
ELSE
IF FRONT = MAX -1
SET FRONT = 0
ELSE
SET FRONT = FRONT + 1
[END of IF]
[END OF IF]

Step 4: EXIT

Let's understand the enqueue and dequeue operation through the diagrammatic representation.

Implementation of circular queue using Array

#include <stdio.h>
# define max 6
int queue[max]; // array declaration
int front=-1;
int rear=-1;
// function to insert an element in a circular queue
void enqueue(int element)
{
if(front==-1 && rear==-1) // condition to check queue is empty
{
front=0;
rear=0;
queue[rear]=element;
}
else if((rear+1)%max==front) // condition to check queue is full
{
printf("Queue is overflow..");
}
else
{
rear=(rear+1)%max; // rear is incremented
queue[rear]=element; // assigning a value to the queue at the rear position.
}
}
// function to delete the element from the queue
int dequeue()
{
if((front==-1) && (rear==-1)) // condition to check queue is empty
{
printf("\nQueue is underflow..");
}
else if(front==rear)
{
printf("\nThe dequeued element is %d", queue[front]);
front=-1;
rear=-1;
}
else
{
printf("\nThe dequeued element is %d", queue[front]);
front=(front+1)%max;
}
}
// function to display the elements of a queue
void display()
{
int i=front;
if(front==-1 && rear==-1)
{
printf("\n Queue is empty..");
}
else
{
printf("\nElements in a Queue are :");
while(i<=rear)
{
printf("%d,", queue[i]);
i=(i+1)%max;
}
}
}
int main()
{
int choice=1,x; // variables declaration
while(choice<4 && choice!=0) // while loop
{
printf("\n Press 1: Insert an element");
printf("\nPress 2: Delete an element");
printf("\nPress 3: Display the element");
printf("\nEnter your choice");
scanf("%d", &choice);
switch(choice)
{
case 1:
printf("Enter the element which is to be inserted");
scanf("%d", &x);
enqueue(x);
break;
case 2:
dequeue();
break;
case 3:
display();
}}
return 0;
}

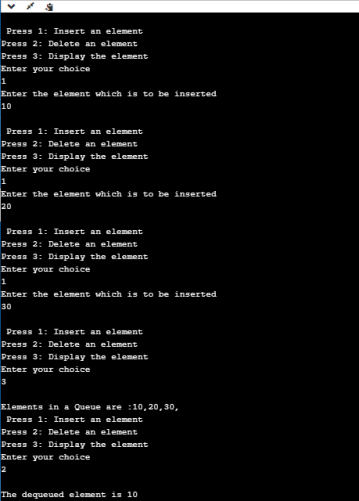
Output:

Circular Queue

Implementation of circular queue using linked list

As we know that linked list is a linear data structure that stores two parts, i.e., data part and the address part where address part contains the address of the next node. Here, linked list is used to implement the circular queue; therefore, the linked list follows the properties of the Queue. When we are implementing the circular queue using linked list then both the enqueue and dequeue operations take O(1) time.

#include <stdio.h>
// Declaration of struct type node
struct node
{
int data;
struct node *next;
};
struct node *front=-1;
struct node *rear=-1;
// function to insert the element in the Queue
void enqueue(int x)
{
struct node *newnode; // declaration of pointer of struct node type.
newnode=(struct node *)malloc(sizeof(struct node)); // allocating the memory to the newnode
newnode->data=x;
newnode->next=0;
if(rear==-1) // checking whether the Queue is empty or not.
{
front=rear=newnode;
rear->next=front;
}
else
{
rear->next=newnode;
rear=newnode;
rear->next=front;
}
}
// function to delete the element from the queue
void dequeue()
{
struct node *temp; // declaration of pointer of node type
temp=front;
if((front==-1)&&(rear==-1)) // checking whether the queue is empty or not
{
printf("\nQueue is empty");
}
else if(front==rear) // checking whether the single element is left in the queue
{
front=rear=-1;
free(temp);
}
else
{
front=front->next;
rear->next=front;
free(temp);
}
}
// function to get the front of the queue
int peek()
{
if((front==-1) &&(rear==-1))
{
printf("\nQueue is empty");
}
else
{
printf("\nThe front element is %d", front->data);
}
}
// function to display all the elements of the queue
void display()
{
struct node *temp;
temp=front;
printf("\n The elements in a Queue are : ");
if((front==-1) && (rear==-1))
{
printf("Queue is empty");
}
else
{
while(temp->next!=front)
{
printf("%d,", temp->data);
temp=temp->next;
}
printf("%d", temp->data);
}
}
void main()
{
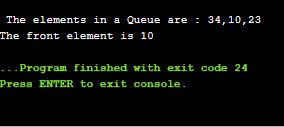
enqueue(34);
enqueue(10);
enqueue(23);
display();
dequeue();
peek();
}

Output:

Circular Queue

Deque

The dequeue stands for Double Ended Queue. In the queue, the insertion takes place from one end while the deletion takes place from another end. The end at which the insertion occurs is known as the rear end whereas the end at which the deletion occurs is known as front end.

Deque

Deque is a linear data structure in which the insertion and deletion operations are performed from both ends. We can say that deque is a generalized version of the queue.

Let's look at some properties of deque.

Deque can be used both as stack and queue as it allows the insertion and deletion operations on both ends.

In deque, the insertion and deletion operation can be performed from one side. The stack follows the LIFO rule in which both the insertion and deletion can be performed only from one end; therefore, we conclude that deque can be considered as a stack.
In deque, the insertion can be performed on one end, and the deletion can be done on another end. The queue follows the FIFO rule in which the element is inserted on one end and deleted from another end. Therefore, we conclude that the deque can also be considered as the queue.

There are two types of Queues, Input-restricted queue, and output-restricted queue.

Input-restricted queue: The input-restricted queue means that some restrictions are applied to the insertion. In input-restricted queue, the insertion is applied to one end while the deletion is applied from both the ends.

Deque

2. Output-restricted queue: The output-restricted queue means that some restrictions are applied to the deletion operation. In an output-restricted queue, the deletion can be applied only from one end, whereas the insertion is possible from both ends.

Deque

Operations on Deque

The following are the operations applied on deque:

Insert at front
Delete from end
insert at rear
delete from rear

Other than insertion and deletion, we can also perform peek operation in deque. Through peek operation, we can get the front and the rear element of the dequeue.

We can perform two more operations on dequeue:

isFull(): This function returns a true value if the stack is full; otherwise, it returns a false value.
isEmpty(): This function returns a true value if the stack is empty; otherwise it returns a false value.

Memory Representation

The deque can be implemented using two data structures, i.e., circular array, and doubly linked list. To implement the deque using circular array, we first should know what is circular array.

What is a circular array?

An array is said to be circular if the last element of the array is connected to the first element of the array. Suppose the size of the array is 4, and the array is full but the first location of the array is empty. If we want to insert the array element, it will not show any overflow condition as the last element is connected to the first element. The value which we want to insert will be added in the first location of the array.

Deque

Fig 18 – Dequeue Example

Applications of Deque

The deque can be used as a stack and queue; therefore, it can perform both redo and undo operations.
It can be used as a palindrome checker means that if we read the string from both ends, then the string would be the same.
It can be used for multiprocessor scheduling. Suppose we have two processors, and each processor has one process to execute. Each processor is assigned with a process or a job, and each process contains multiple threads. Each processor maintains a deque that contains threads that are ready to execute. The processor executes a process, and if a process creates a child process then that process will be inserted at the front of the deque of the parent process. Suppose the processor P2 has completed the execution of all its threads then it steals the thread from the rear end of the processor P1 and adds to the front end of the processor P2. The processor P2 will take the thread from the front end; therefore, the deletion takes from both the ends, i.e., front and rear end. This is known as the A-steal algorithm for scheduling.

Implementation of Deque using a circular array

The following are the steps to perform the operations on the Deque:

Enqueue operation

Initially, we are considering that the deque is empty, so both front and rear are set to -1, i.e., f = -1 and r = -1.
As the deque is empty, so inserting an element either from the front or rear end would be the same thing. Suppose we have inserted element 1, then front is equal to 0, and the rear is also equal to 0.

Deque

3. Suppose we want to insert the next element from the rear. To insert the element from the rear end, we first need to increment the rear, i.e., rear=rear+1. Now, the rear is pointing to the second element, and the front is pointing to the first element.

Deque

4. Suppose we are again inserting the element from the rear end. To insert the element, we will first increment the rear, and now rear points to the third element.

Deque

5. If we want to insert the element from the front end, and insert an element from the front, we have to decrement the value of front by 1. If we decrement the front by 1, then the front points to -1 location, which is not any valid location in an array. So, we set the front as (n -1), which is equal to 4 as n is 5. Once the front is set, we will insert the value as shown in the below figure:

Deque

Dequeue Operation

If the front is pointing to the last element of the array, and we want to perform the delete operation from the front. To delete any element from the front, we need to set front=front+1. Currently, the value of the front is equal to 4, and if we increment the value of front, it becomes 5 which is not a valid index. Therefore, we conclude that if front points to the last element, then front is set to 0 in case of delete operation.

Deque

2. If we want to delete the element from rear end then we need to decrement the rear value by 1, i.e., rear=rear-1 as shown in the below figure:

Deque

3. If the rear is pointing to the first element, and we want to delete the element from the rear end then we have to set rear=n-1 where n is the size of the array as shown in the below figure:

Deque

Let's create a program of deque.

The following are the six functions that we have used in the below program:

enqueue_front(): It is used to insert the element from the front end.
enqueue_rear(): It is used to insert the element from the rear end.
dequeue_front(): It is used to delete the element from the front end.
dequeue_rear(): It is used to delete the element from the rear end.
getfront(): It is used to return the front element of the deque.
getrear(): It is used to return the rear element of the deque.

#define size 5
#include <stdio.h>
int deque[size];
int f=-1, r=-1;
// enqueue_front function will insert the value from the front
void enqueue_front(int x)
{
if((f==0 && r==size-1) || (f==r+1))
{
printf("deque is full");
}
else if((f==-1) && (r==-1))
{
f=r=0;
deque[f]=x;
}
else if(f==0)
{
f=size-1;
deque[f]=x;
}
else
{
f=f-1;
deque[f]=x;
}
}
// enqueue_rear function will insert the value from the rear
void enqueue_rear(int x)
{
if((f==0 && r==size-1) || (f==r+1))
{
printf("deque is full");
}
else if((f==-1) && (r==-1))
{
r=0;
deque[r]=x;
}
else if(r==size-1)
{
r=0;
deque[r]=x;
}
else
{
r++;
deque[r]=x;
}
}
// display function prints all the value of deque.
void display()
{
int i=f;
printf("\n Elements in a deque : ");
while(i!=r)
{
printf("%d ",deque[i]);
i=(i+1)%size;
}
printf("%d",deque[r]);
}
// getfront function retrieves the first value of the deque.
void getfront()
{
if((f==-1) && (r==-1))
{
printf("Deque is empty");
}
else
{
printf("\nThe value of the front is: %d", deque[f]);
}
}
// getrear function retrieves the last value of the deque.
void getrear()
{
if((f==-1) && (r==-1))
{
printf("Deque is empty");
}
else
{
printf("\nThe value of the rear is: %d", deque[r]);
}
}
// dequeue_front() function deletes the element from the front
void dequeue_front()
{
if((f==-1) && (r==-1))
{
printf("Deque is empty");
}
else if(f==r)
{
printf("\nThe deleted element is %d", deque[f]);
f=-1;
r=-1;
}
else if(f==(size-1))
{
printf("\nThe deleted element is %d", deque[f]);
f=0;
}
else
{
printf("\nThe deleted element is %d", deque[f]);
f=f+1;
}
}
// dequeue_rear() function deletes the element from the rear
void dequeue_rear()
{
if((f==-1) && (r==-1))
{
printf("Deque is empty");
}
else if(f==r)
{
printf("\nThe deleted element is %d", deque[r]);
f=-1;
r=-1;
}
else if(r==0)
{
printf("\nThe deleted element is %d", deque[r]);
r=size-1;
}
else
{
printf("\nThe deleted element is %d", deque[r]);
r=r-1;
}
}
int main()
{
// inserting a value from the front.
enqueue_front(2);
// inserting a value from the front.
enqueue_front(1);
// inserting a value from the rear.
enqueue_rear(3);
// inserting a value from the rear.
enqueue_rear(5);
// inserting a value from the rear.
enqueue_rear(8);
// Calling the display function to retrieve the values of deque
display();
// Retrieve the front value
getfront();
// Retrieve the rear value.
getrear();
// deleting a value from the front
dequeue_front();
//deleting a value from the rear
dequeue_rear();
// Calling the display function to retrieve the values of deque
display();
return 0;
}

Output:

Deque

What is a priority queue?

A priority queue is an abstract data type that behaves similarly to the normal queue except that each element has some priority, i.e., the element with the highest priority would come first in a priority queue. The priority of the elements in a priority queue will determine the order in which elements are removed from the priority queue.

The priority queue supports only comparable elements, which means that the elements are either arranged in an ascending or descending order.

For example, suppose we have some values like 1, 3, 4, 8, 14, 22 inserted in a priority queue with an ordering imposed on the values is from least to the greatest. Therefore, the 1 number would be having the highest priority while 22 will be having the lowest priority.

Characteristics of a Priority queue

A priority queue is an extension of a queue that contains the following characteristics:

Every element in a priority queue has some priority associated with it.
An element with the higher priority will be deleted before the deletion of the lesser priority.
If two elements in a priority queue have the same priority, they will be arranged using the FIFO principle.

Let's understand the priority queue through an example.

We have a priority queue that contains the following values:

1, 3, 4, 8, 14, 22

All the values are arranged in ascending order. Now, we will observe how the priority queue will look after performing the following operations:

poll(): This function will remove the highest priority element from the priority queue. In the above priority queue, the '1' element has the highest priority, so it will be removed from the priority queue.
add(2): This function will insert '2' element in a priority queue. As 2 is the smallest element among all the numbers so it will obtain the highest priority.
poll(): It will remove '2' element from the priority queue as it has the highest priority queue.
add(5): It will insert 5 element after 4 as 5 is larger than 4 and lesser than 8, so it will obtain the third highest priority in a priority queue.

Types of Priority Queue

There are two types of priority queue:

Ascending order priority queue: In ascending order priority queue, a lower priority number is given as a higher priority in a priority. For example, we take the numbers from 1 to 5 arranged in an ascending order like 1,2,3,4,5; therefore, the smallest number, i.e., 1 is given as the highest priority in a priority queue.

Priority Queue

Descending order priority queue: In descending order priority queue, a higher priority number is given as a higher priority in a priority. For example, we take the numbers from 1 to 5 arranged in descending order like 5, 4, 3, 2, 1; therefore, the largest number, i.e., 5 is given as the highest priority in a priority queue.

Priority Queue

Representation of priority queue

Now, we will see how to represent the priority queue through a one-way list.

We will create the priority queue by using the list given below in which INFO list contains the data elements, PRN list contains the priority numbers of each data element available in the INFO list, and LINK basically contains the address of the next node.

Priority Queue

Let's create the priority queue step by step.

In the case of priority queue, lower priority number is considered the higher priority, i.e., lower priority number = higher priority.

Step 1: In the list, lower priority number is 1, whose data value is 333, so it will be inserted in the list as shown in the below diagram:

Step 2: After inserting 333, priority number 2 is having a higher priority, and data values associated with this priority are 222 and 111. So, this data will be inserted based on the FIFO principle; therefore 222 will be added first and then 111.

Step 3: After inserting the elements of priority 2, the next higher priority number is 4 and data elements associated with 4 priority numbers are 444, 555, 777. In this case, elements would be inserted based on the FIFO principle; therefore, 444 will be added first, then 555, and then 777.

Step 4: After inserting the elements of priority 4, the next higher priority number is 5, and the value associated with priority 5 is 666, so it will be inserted at the end of the queue.

Priority Queue

Implementation of Priority Queue

The priority queue can be implemented in four ways that include arrays, linked list, heap data structure and binary search tree. The heap data structure is the most efficient way of implementing the priority queue, so we will implement the priority queue using a heap data structure in this topic. Now, first we understand the reason why heap is the most efficient way among all the other data structures.

Analysis of complexities using different implementations

Implementation	Add	Remove	peek
Linked list	O(1)	O(n)	O(n)
Binary heap	O(logn)	O(logn)	O(1)
Binary search tree	O(logn)	O(logn)	O(1)

What is Heap?

A heap is a tree-based data structure that forms a complete binary tree, and satisfies the heap property. If A is a parent node of B, then A is ordered with respect to the node B for all nodes A and B in a heap. It means that the value of the parent node could be more than or equal to the value of the child node, or the value of the parent node could be less than or equal to the value of the child node. Therefore, we can say that there are two types of heaps:

Max heap: The max heap is a heap in which the value of the parent node is greater than the value of the child nodes.

Priority Queue

Min heap: The min heap is a heap in which the value of the parent node is less than the value of the child nodes.

Priority Queue

Both the heaps are the binary heap, as each has exactly two child nodes.

Priority Queue Operations

The common operations that we can perform on a priority queue are insertion, deletion and peek. Let's see how we can maintain the heap data structure.

Inserting the element in a priority queue (max heap)

If we insert an element in a priority queue, it will move to the empty slot by looking from top to bottom and left to right.

If the element is not in a correct place then it is compared with the parent node; if it is found out of order, elements are swapped. This process continues until the element is placed in a correct position.

Priority Queue

Removing the minimum element from the priority queue

As we know that in a max heap, the maximum element is the root node. When we remove the root node, it creates an empty slot. The last inserted element will be added in this empty slot. Then, this element is compared with the child nodes, i.e., left-child and right child, and swap with the smaller of the two. It keeps moving down the tree until the heap property is restored.

Applications of Priority queue

The following are the applications of the priority queue:

It is used in the Dijkstra's shortest path algorithm.
It is used in prim's algorithm
It is used in data compression techniques like Huffman code.
It is used in heap sort.
It is also used in operating system like priority scheduling, load balancing and interrupt handling.

Program to create the priority queue using the binary max heap.

#include <stdio.h>
#include <stdio.h>
int heap[40];
int size=-1;
// retrieving the parent node of the child node
int parent(int i)
{
return (i - 1) / 2;
}
// retrieving the left child of the parent node.
int left_child(int i)
{
return i+1;
}
// retrieving the right child of the parent
int right_child(int i)
{
return i+2;
}
// Returning the element having the highest priority
int get_Max()
{
return heap[0];
}
//Returning the element having the minimum priority
int get_Min()
{
return heap[size];
}
// function to move the node up the tree in order to restore the heap property.
void moveUp(int i)
{
while (i > 0)
{
// swapping parent node with a child node
if(heap[parent(i)] < heap[i]) {
int temp;
temp=heap[parent(i)];
heap[parent(i)]=heap[i];
heap[i]=temp;
}
// updating the value of i to i/2
i=i/2;
}
}
//function to move the node down the tree in order to restore the heap property.
void moveDown(int k)
{
int index = k;
// getting the location of the Left Child
int left = left_child(k);
if (left <= size && heap[left] > heap[index]) {
index = left;
}
// getting the location of the Right Child
int right = right_child(k);
if (right <= size && heap[right] > heap[index]) {
index = right;
}
// If k is not equal to index
if (k != index) {
int temp;
temp=heap[index];
heap[index]=heap[k];
heap[k]=temp;
moveDown(index);
}
}
// Removing the element of maximum priority
void removeMax()
{
int r= heap[0];
heap[0]=heap[size];
size=size-1;
moveDown(0);
}
//inserting the element in a priority queue
void insert(int p)
{
size = size + 1;
heap[size] = p;
// move Up to maintain heap property
moveUp(size);
}
//Removing the element from the priority queue at a given index i.
void delete(int i)
{
heap[i] = heap[0] + 1;
// move the node stored at ith location is shifted to the root node
moveUp(i);
// Removing the node having maximum priority
removeMax();
}
int main()
{
// Inserting the elements in a priority queue
insert(20);
insert(19);
insert(21);
insert(18);
insert(12);
insert(17);
insert(15);
insert(16);
insert(14);
int i=0;
printf("Elements in a priority queue are : ");
for(int i=0;i<=size;i++)
{
printf("%d ",heap[i]);
}
delete(2); // deleting the element whose index is 2.
printf("\nElements in a priority queue after deleting the element are : ");
for(int i=0;i<=size;i++)
{
printf("%d ",heap[i]);
}
int max=get_Max();
printf("\nThe element which is having the highest priority is %d: ",max);
int min=get_Min();
printf("\nThe element which is having the minimum priority is : %d",min);
return 0;
}

In the above program, we have created the following functions:

int parent(int i): This function returns the index of the parent node of a child node, i.e., i.
int left_child(int i): This function returns the index of the left child of a given index, i.e., i.
int right_child(int i): This function returns the index of the right child of a given index, i.e., i.
void moveUp(int i): This function will keep moving the node up the tree until the heap property is restored.
void moveDown(int i): This function will keep moving the node down the tree until the heap property is restored.
void removeMax(): This function removes the element which is having the highest priority.
void insert(int p): It inserts the element in a priority queue which is passed as an argument in a function.
void delete(int i): It deletes the element from a priority queue at a given index.
int get_Max(): It returns the element which is having the highest priority, and we know that in max heap, the root node contains the element which has the largest value, and highest priority.
int get_Min(): It returns the element which is having the minimum priority, and we know that in max heap, the last node contains the element which has the smallest value, and lowest priority.

Output

Priority Queue

Key takeaway

Reference

1 Data structure & algorithm analysis in C by Mark Allen Weiss published by Pearson Education (LPE)

2 Introduction to Data structure in C by A.N. Kathie published by Pearson Education (LPE)

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined