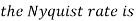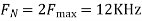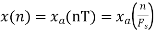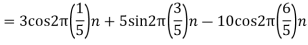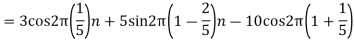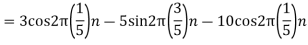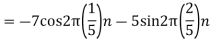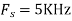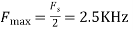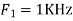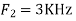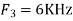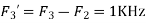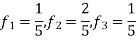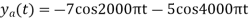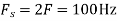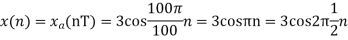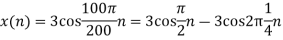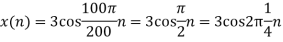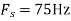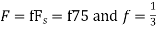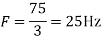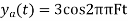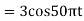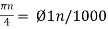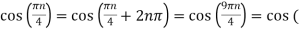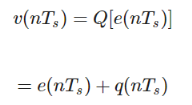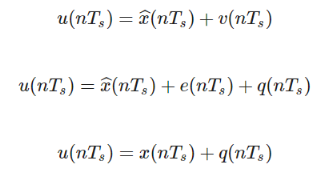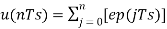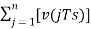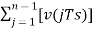UNIT - 2
Source Coding
The sampling theorem, which is also called as Nyquist theorem, delivers the theory of sufficient sample rate in terms of bandwidth for the class of functions that are bandlimited.
The sampling theorem states that, “a signal can be exactly reproduced if it is sampled at the rate fs which is greater than twice the maximum frequency W.”
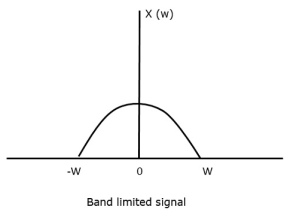
Let us consider a band-limited signal, i.e., a signal whose value is non-zero between some –W and W Hertz.
Such a signal is represented as x(f)=0 for ∣f∣>W
For the continuous-time signal x(t), the band-limited signal in frequency domain, can be represented as shown in the following figure.
|
Fig. 1: Band limited signal
If the signal x(t) is sampled above the Nyquist rate, the original signal can be recovered, and if it is sampled below the Nyquist rate, the signal cannot be recovered.
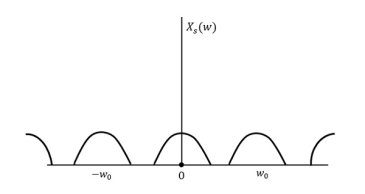
The following figure explains a signal, if sampled at a higher rate than 2w in the frequency domain.
|
Fig.2: Sampled signal
The above figure shows the Fourier transform of a signal xs(t).
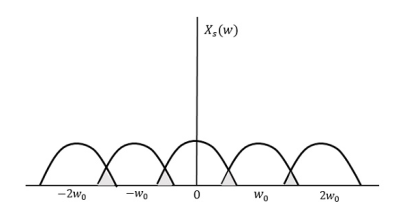
If fs<2W
The resultant pattern will look like the following figure.
|
Fig.3: Resultant waveform
Here, the over-lapping of information is done, which leads to mixing up and loss of information. This unwanted phenomenon of over-lapping is called as Aliasing.
Key Takeaways:
- If the signal x(t) is sampled above the Nyquist rate, the original signal can be recovered, and if it is sampled below the Nyquist rate, the signal cannot be recovered.
- The over-lapping of information is done, which leads to mixing up and loss of information. This unwanted phenomenon of over-lapping is called as Aliasing.
Numerical:
- The continuous-time signal x(t) = cos(200πt) is used as the input for a CD converter with the sampling period 1/300 sec. Determine the resultant discrete-time signal x[n].
Solution:
We know, X[n] =x(nT) = cos(200πnT) = cos(2πn/3) , where n= -1,0,1,2……
The frequency in x(t) is 200π rad/s while that of x[n] is 2π/3.
2. Determine the Nyquist frequency and Nyquist rate for the continuous-time signal x(t) which has the form of: X(t) = 1+ sin(2000πt) + cos (4000πt)
Solution:
The frequencies are 0, 2000π and 4000π. The Nyquist frequency is 4000π rad/s and the Nyquist rate is 8000π rad/s.
|
2. Consider an analog signal.
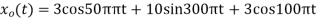
Solution.
The frequency in the analog signal
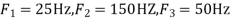
The largest frequency is
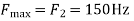
The Nyquist rate is

3. The analog signal
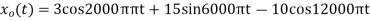
- What is the Nyquist rate for this signal?
- Using a sampling rate
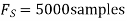 . What is discrete time signal obtained after sampling?
. What is discrete time signal obtained after sampling? - What is analog signal
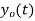 we can reconstruct from the samples if we use ideal interpolation?
we can reconstruct from the samples if we use ideal interpolation?
Solution.
2. For
For Hence
So that normalizing frequencies are
The analog signal that we can recover is
Which is different than the original signal
|
4. 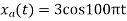
- Find the minimum sampling rate required to avoid aliasing.
- If
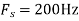 , what is the discrete time signal after sampling?
, what is the discrete time signal after sampling? - If
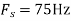 , what is the discrete time signal after sampling?
, what is the discrete time signal after sampling? - What is the frequency F of a sinusoidal that yields sampling identical to obtained in part c?
Solution. a. 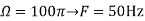
The minimum sampling rate is
And the discrete time signal is
b. if
c. If Fs=75Hz , the discrete time signal is
d. For the sampling rate
So, the analog sinusoidal signal is
|
5. Suppose a continuous-time signal x(t) = cos (Ø0t) is sampled at a sampling frequency of 1000Hz to produce x[n]: x[n] = cos(πn/4)
Determine 2 possible positive values of Ø0, say, Ø1 and Ø2. Discuss if cos(Ø1t) or cos(Ø2t) will be obtained when passing through the DC converter.
Solution:
Taking T= 1/1000s cos(πn/4) =x[n] = x(nT) = cos (Ø0n/1000) Ø1 is easily computed as Ø1 = 250π
Ø2 can be obtained by noting the periodicity of a sinusoid:
Ø2 = 2250π
|
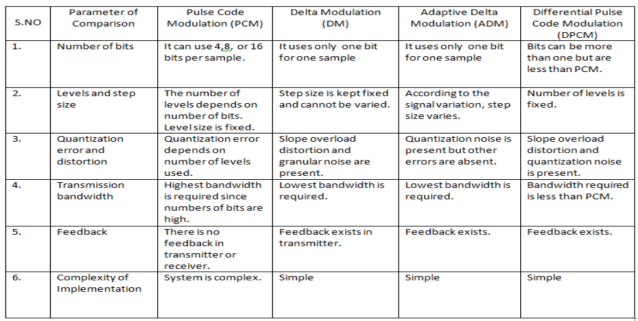
There are two types of Quantization - Uniform Quantization and Non-Uniform Quantization.
The type of quantization in which the quantization levels are uniformly spaced is termed as a Uniform Quantization. The type of quantization in which the quantization levels are unequal and mostly the relation between them is logarithmic, is termed as a Non-uniform Quantization.
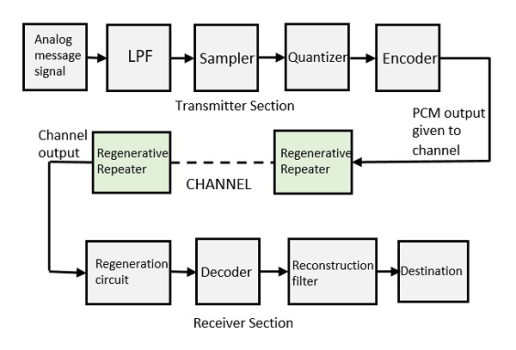
In Pulse Code Modulation, the message signal is represented by a sequence of coded pulses. This message signal is achieved by representing the signal in discrete form in both time and amplitude.
The transmitter section comprises of Sampling, Quantizing and Encoding. The low pass filter prior to sampling prevents aliasing of the message signal.
The basic operations in the receiver section are regeneration of impaired signals, decoding, and reconstruction of the quantized pulse train.
|
Fig.4: PCM
This filter eliminates the high frequency components present in the input analog signal to avoid aliasing of the message signal.
It helps to collect the sample data at instantaneous values of message signal, so as to reconstruct the original signal. The sampling rate must be in accordance with the sampling theorem.
It reduces excessive bits and confines the data. It reduces the redundant bits and compresses the value of the sampled output.
The digitization of analog signal is done by the encoder. It designates each quantized level by a binary code. Encoding minimizes the bandwidth used.
It increases the signal strength. The output of the channel also has one regenerative repeater circuit, to compensate the signal loss and reconstruct the signal, and also to increase its strength.
The decoder circuit decodes the pulse coded waveform to reproduce the original signal. This circuit acts as the demodulator.
After the digital-to-analog conversion is done by the regenerative circuit and the decoder, a low-pass filter is employed, called as the reconstruction filter to get back the original signal.
Hence, the Pulse Code Modulator circuit digitizes the given analog signal, codes it and samples it, and then transmits it in an analog form. This whole process is repeated in a reverse pattern to obtain the original signal.
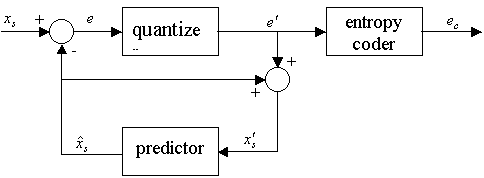
Differential pulse code modulation (DPCM) is a procedure of converting an analog into a digital signal in which an analog signal is sampled and then the difference between the actual sample value and its predicted value (predicted value is based on previous sample or samples) is quantized and then encoded forming a digital value.
DPCM code words represent differences between samples unlike PCM where code words represented a sample value.
Basic concept of DPCM - coding a difference, is based on the fact that most source signals show significant correlation between successive samples so encoding uses redundancy in sample values which implies lower bit rate.
Realization of basic concept (described above) is based on a technique in which we have to predict current sample value based upon previous samples (or sample) and we have to encode the difference between actual value of sample and predicted value (the difference between samples can be interpreted as prediction error).
Because it's necessary to predict sample value DPCM is form of predictive coding.
DPCM compression depends on the prediction technique, well-conducted prediction techniques lead to good compression rates, in other cases DPCM could mean expansion comparing to regular PCM encoding.
|
Fig.5: DPCM
Key Takeaways:
- DPCM code words represent differences between samples unlike PCM where code words represented a sample value.
- Basic concept of DPCM - coding a difference, is based on the fact that most source signals show significant correlation between successive samples so encoding uses redundancy in sample values which implies lower bit rate.
Quantizer Output is represented as –
Where q (nTs) is the quantization error Predictor input is the sum of quantizer output and predictor output,
|
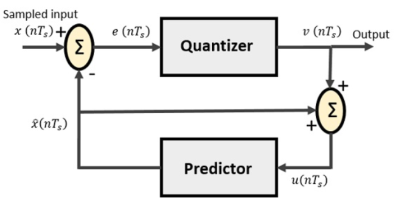
Differential PCM (DPCM) is based on the quantization of the difference between a sample value and the prediction of that sample value using the previous sample values. Since this difference (prediction error) is much smaller than the sample value, fewer bits are required to quantize it. This means that DPCM can achieve performance levels at lower bit rates than PCM.
The prediction filter, as shown in Figure, is a tapped-delay-line (transversal filter) where the predicted value is modeled as a linear combination of past-quantized samples. In the design of the prediction filter, the minimum mean-squared error criterion for best prediction is employed, where the prediction coefficients (tap gains) are determined from the statistical correlation among various samples.
|
Fig.6: Predictor
The sample rate is twice the 4 kHz bandwidth required for a toll-quality voice ... of bits in the PCM word (M = 2n), fs is the sampling rate, and R is the bit rate.
The type of modulation, where the sampling rate is much higher and in which the step size after quantization is of a smaller value Δ, such a modulation is termed as delta modulation.
- The quality is moderate.
- The design of the modulator and the demodulator is simple.
- The stair-case approximation of output waveform.
- The step-size is very small, i.e., Δ delta.
- The bit rate can be decided by the user.
- This involves simpler implementation.
Delta Modulation is a simplified form of DPCM technique, also viewed as 1-bit DPCM scheme. As the sampling interval is reduced, the signal correlation will be higher.
Delta Modulator
The Delta Modulator comprises of a 1-bit quantizer and a delay circuit along with two summer circuits. Following is the block diagram of a delta modulator.
|
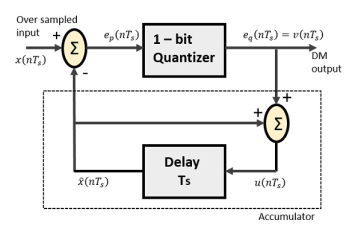
Fig.7: Delta Modulator
The predictor circuit in DPCM is replaced by a simple delay circuit in DM.
From the above diagram, we have the notations as −
- x(nTs)= over sampled input
- ep(nTs) = summer output and quantizer input
- eq(nTs) = quantizer output = v(nTs)
- xˆ(nTs) = output of delay circuit
- u(nTs) = input of delay circuit
Using these notations, now we shall try to figure out the process of delta modulation.
ep(nTs)=x(nTs)−xˆ(nTs) ---------equation 1 =x(nTs)−u([n−1]Ts =x(nTs)−[xˆ[[n−1]Ts]+v[[n−1]Ts]] -------equation 2 Further, v(nTs)=eq(nTs)=S.sig.[ep(nTs)] ---------equation 3 u(nTs)=xˆ(nTs)+eq(nTs) Where,
Hence, u(nTs)=u([n−1]Ts)+v(nTs) ---------equation 4 Which means, The present input of the delay unit = The previous output of the delay unit + the present quantizer output the present quantizer output Assuming zero condition of Accumulation,
Accumulated version of DM output = Now, note that xˆ(nTs)=u([n−1]Ts) =
|
Delay unit output is an Accumulator output lagging by one sample.
From equations 5 & 6, we get a possible structure for the demodulator.
A Stair-case approximated waveform will be the output of the delta modulator with the step-size as delta (Δ). The output quality of the waveform is moderate.
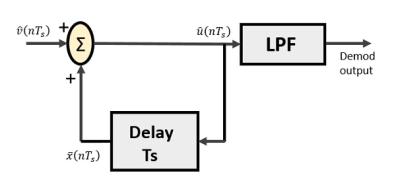
Delta Demodulator
The delta demodulator comprises of a low pass filter, a summer, and a delay circuit. The predictor circuit is eliminated here and hence no assumed input is given to the demodulator.
Following is the diagram for delta demodulator.
|
Fig.8: Delta Demodulator
From the above diagram, we have the notations as −
- vˆ(nTs) is the input sample
- uˆ(nTs) is the summer output
- x¯(nTs) is the delayed output
A binary sequence will be given as an input to the demodulator. The stair-case approximated output is given to the LPF.
Low pass filter is used for many reasons, but the prominent reason is noise elimination for out-of-band signals. The step-size error that may occur at the transmitter is called granular noise, which is eliminated here. If there is no noise present, then the modulator output equals the demodulator input.
- 1-bit quantizer
- Very easy design of the modulator and the demodulator
- Slope Over load distortion (when Δ is small)
- Granular noise (when Δ is large)
In digital modulation, we have come across certain problem of determining the step-size, which influences the quality of the output wave.
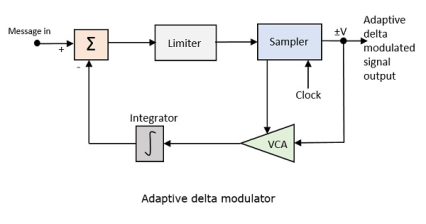
A larger step-size is needed in the steep slope of modulating signal and a smaller step size is needed where the message has a small slope. The minute details get missed in the process. So, it would be better if we can control the adjustment of step-size, according to our requirement in order to obtain the sampling in a desired fashion. This is the concept of Adaptive Delta Modulation.
Following is the block diagram of Adaptive delta modulator.
|
Fig. 9: Adaptive delta modulator
The gain of the voltage-controlled amplifier is adjusted by the output signal from the sampler. The amplifier gain determines the step-size and both are proportional.
ADM quantizes the difference between the value of the current sample and the predicted value of the next sample. It uses a variable step height to predict the next values, for the faithful reproduction of the fast-varying values.
|
References:
1. B.P. Lathi, “Modern Digital and Analog communication Systems”, 4th Edition, Oxford University Press, 2010.
2. Rishabh Anand, Communication Systems, Khanna Publishing House, Delhi.