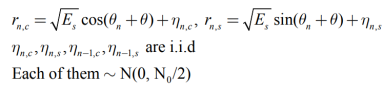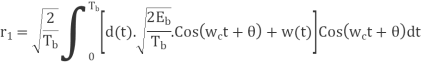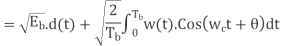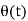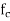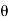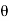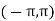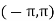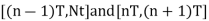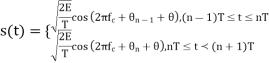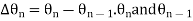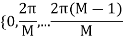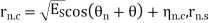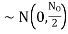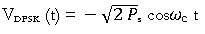4.1 ASK | unit 4 band pass modulation demodulation

UNIT - 4

Band pass Modulation & Demodulation

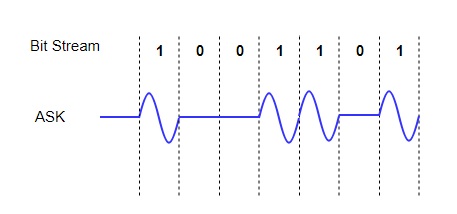
In ASK, the amplitude of the signal is varied to represent the signal levels, while frequency and phase remains constant. In order to represent 0 and 1, two different amplitudes are used.

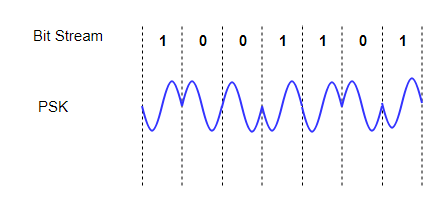
Bit Stream

Fig. 1: ASK

4.2 PSK

In this, the phase of the carrier signal is modulated to represent the signal levels, while amplitude and frequency remains constant.

Binary Phase Shift Keying (BPSK) is the simplest form of PSK where there are two signal elements represented by two different phases.

In Quadrature PSK (QPSK), two bits of information are transmitted per symbol by using four different phases.

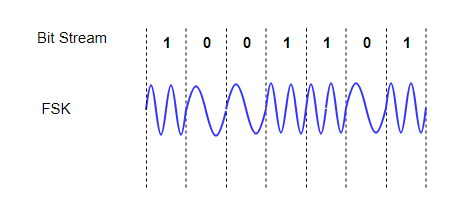
Bit Stream

Fig. 2: ASK

4.3 FSK

In FSK, the frequency of the signal is modulated to represent the signal levels, while amplitude and phase remains constant.

To represent the signal levels 0 and 1, two different frequencies are used.

Bit Stream

Fig. 3: ASK

Key Takeaways:

In ASK, the amplitude of the signal is varied to represent the signal levels, while frequency and phase remains constant.
In FSK, the frequency of the signal is modulated to represent the signal levels, while amplitude and phase remains constant.
In PSK, the phase of the carrier signal is modulated to represent the signal levels, while amplitude and frequency remains constant.

4.4 DPSK

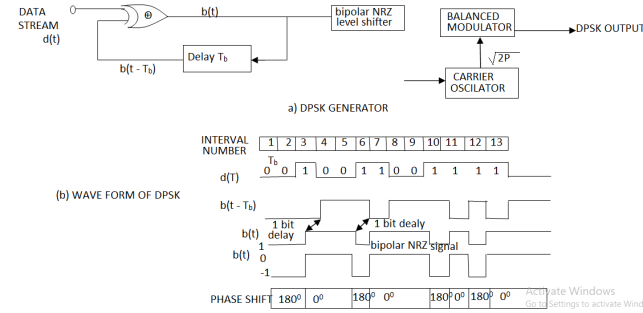
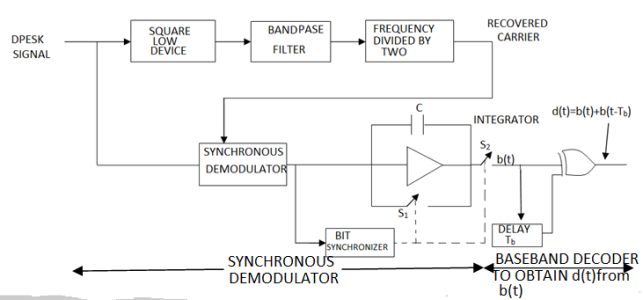
Fig.4: DPSK generation

Key Takeaways:

Here, the phase of the modulated signal is shifted relative to the previous signal element. No reference signal is considered here. The signal phase follows the high or low state of the previous element. This DPSK technique doesn’t need a reference oscillator.

4.5 QPSK

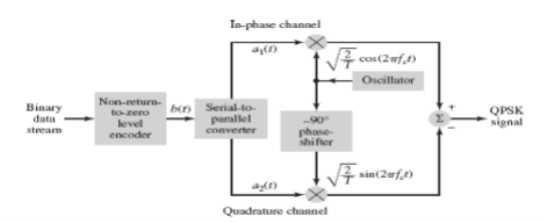
GENERATION AND COHERENT DETECTION OF QPSK SIGNALS

(i) Generation

The QPSK Modulator uses a bit-splitter, two multipliers with local oscillator, a 2-bit serial to parallel converter, and a summer circuit.

Fig.5: QPSK generation

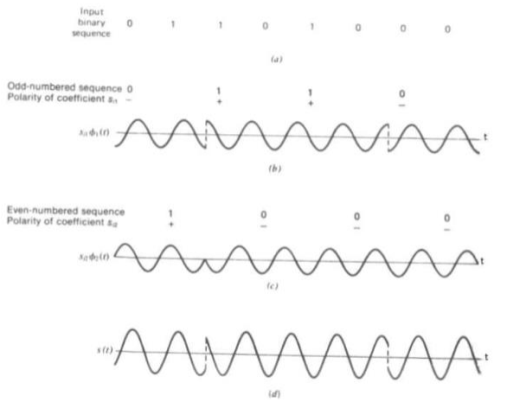
At the modulator’s input, the message signal’s even bits (i.e., 2nd bit, 4th bit, 6th bit, etc.) and odd bits (i.e., 1st bit, 3rd bit, 5th bit, etc.) are separated by the bits splitter and are multiplied with the same carrier to generate odd BPSK (called as PSKI) and even BPSK (called as PSKQ). The PSKQ signal is anyhow phase shifted by 90° before being modulated.

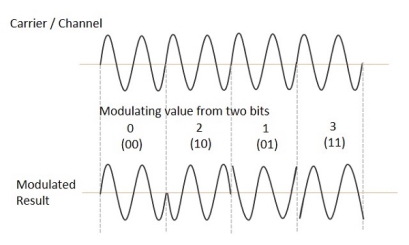
The QPSK waveform for two-bits input is as follows, which shows the modulated result for different instances of binary inputs.

QPSK Waveform

Fig.6: QPSK output

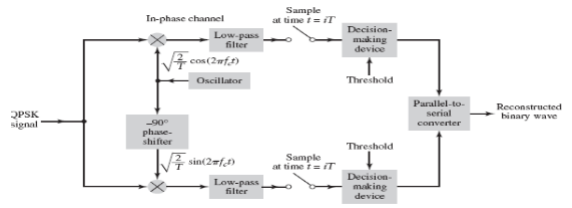
(ii) Detection

The QPSK Demodulator uses two product demodulator circuits with local oscillator, two band pass filters, two integrator circuits, and a 2-bit parallel to serial converter.

Fig.7: QPSK detectors

The two product detectors at the input of demodulator simultaneously demodulate the two BPSK signals. The pair of bits are recovered here from the original data. These signals after processing are passed to the parallel to serial converter.

Fig.8: QPSK output

4.6 BPSK

GENERATION AND COHERENT DETECTION OF BPSK SIGNALS

(i) Generation

To generate the BPSK signal, we build on the fact that the BPSK signal is a special case of DSB-SC modulation. Specifically, we use a product modulator consisting of two components.

(i) Non-return-to-zero level encoder, whereby the input binary data sequence is encoded inpolar form with symbols 1 and 0 represented by the constant-amplitude.

(ii) Product modulator, which multiplies the level encoded binary wave by the sinusoidalcarrier of amplitude to produce the BPSK signal. The timing pulses used to generate the level encoded binary wave and the sinusoidal carrier wave are usually, but not necessarily, extracted from a common master clock.

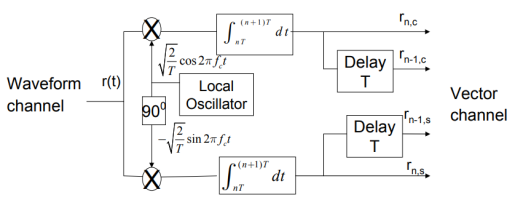
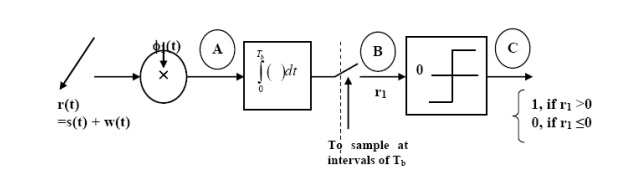
(ii) Detection

To detect the original binary sequence of 1s and 0s, the BPSK signal at the channel output is applied to a receiver that consists of four sections

(a)Product modulator, which is also supplied with a locally generated reference signal thatis a replica of the carrier wave

(b)Low-pass filter, designed to remove the double-frequency components of the product modulator output (i.e., the components centered on) and pass the zero-frequency components.

(c)Sampler, which uniformly samples the output of the low-pass filter at where; the localclock governing the operation of the sampler issynchronized with the clock responsible for bit-timing in the transmitter.

(d)Decision-making device, which compares the sampled value of the low-pass filtersoutput to an externally supplied threshold, every seconds. If the threshold is exceeded, the device decides in favor of symbol 1; otherwise, it decides in favor of symbol 0. levels.

The signal B is

4.7DPSK

=amplitude information

=phase information

=the carrier frequency

=the phase shift introduce by the channel

- In coherent communication, is known to receivers

- In non coherent communications, is unknown to receivers and assumed to be a random variable distributed uniformly over .

- The phase shift is treated as a random variable distributed over and no phase estimation is provided at the receiver.

- We have now concerned with non coherent communications.

- The phase shift is the same during two consecutive signals transmission intervals

- The transmission signal s(t) in the interval is

are independent. Both of them take values uniformly over

ηn.c,ηn.s,ηn-1,c,ηn-1,s are i.i.d

Each of them

4.8 DEPSK

The transmitter (modulator) of a DEPSK system is identical to the DPSK transmitter.
The differential phase shift keying (DPSK) is a modulation of BPSK.
Fig shows the block diagram of DPSK generator and the relevant waveforms.

$C:\Users\Ssd\Desktop\BOOK DIADRAM 1.png$

Operation:

d (t) represents the data stream which is to be transmitted. It is applied to one input of an EX-OR logic gate.
The EX-OR gate output “b (t)” is delayed by one-bit period Tb and applied to the other input of the EX-OR gate. The delayed output is represented by “b(t−Tb)b(t−Tb)”
Depending on the values of “d (t)” and “b(t−Tb)b(t−Tb)”,the EX-OR gate produces the output sequence “b (t)”.The waveforms for DPSK generator have been drawn by arbitrarily that in the first interval b (0)=0.
Output of EX-OR gate is then applied to a bipolar NRZ level shifter which converts “b(t)” to a bipolar level signal b’(t) as shown in the fig.

enter image description here

This bipolar NRZ signal b’(t) is then multiplied with the carrier signal to produce the DPSK signal. The DPSK output signal is mathematically expressed as:

VDPSK(t)=b′(t)∗2Ps−−−√cosωCt

VDPSK(t)=b′(t)∗2PscosωCt

So when b(t) =1 , b’(t) =1 hence

VDPSK(t)=VDPSK(t)=b'(t)∗2Ps−−−√cosωCt∗2PscosωCt

That means no phase shift has been introduced.

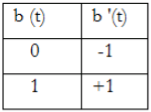
Bt when b(t) =0, b’(t)= -1 hence

enter image description here

Thus 180-degree phase shift is introduced to represent b(t) =0
The block diagram of DEPSK receiver is shown below. It shows that the signal b (t) is recovered from the received signal, using the synchronous demodulation technique. This is same as the BPSK detection. Once the signal b (t) is recovered, it is applied to one input of an EX-OR gate.
The signal b(t) is also applied to a time delay circuit and the delayed signal b(t−Tb)b(t−Tb) is applied to the other input of the EX-OR gate as shown below

$C:\Users\Ssd\Desktop\book diagram 2.png$

If b(t)= b(t−Tb)b(t−Tb) then output of the EX-OR gate will be 0

d (t) =0 ………if b(t)=b(t−Tb)(t)=b(t−Tb)

And if b(t) = b(t−Tb)b(t−Tb) then output of the EX-OR gate will be 1

d (t) =1 ……… b(t) = b(t−Tb)

4.9 QAM

QAM is a combination of ASK and PSK. Here, both the amplitude and the phase are are varied to transmit more bits per symbol.

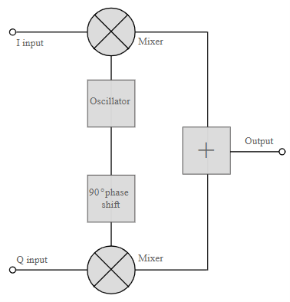
The QAM modulator essentially follows the idea that can be seen from the basic QAM theory where there are two carrier signals with a phase shift of 90° between them. These are then amplitude modulated with the two data streams known as the I or In-phase and the Q or quadrature data streams. These are generated in the baseband processing area.

Basic QAM I-Q modulator circuit

The two resultant signals are summed and then processed as required in the RF signal chain, typically converting them in frequency to the required final frequency and amplifying them as required.

Fig.10: Basic QAM

It is worth noting that as the amplitude of the signal varies any RF amplifiers must be linear to preserve the integrity of the signal. Any non-linearities will alter the relative levels of the signals and alter the phase difference, thereby distorting he signal and introducing the possibility of data errors.

Basic QAM I-Q demodulator circuit

The basic modulator assumes that the two quadrature signals remain exactly in quadrature.

A further requirement is to derive a local oscillator signal for the demodulation that is exactly on the required frequency for the signal. Any frequency offset will be a change in the phase of the local oscillator signal with respect to the two double sideband suppressed carrier constituents of the overall signal.

Systems include circuitry for carrier recovery that often utilises a phase locked loop - some even have an inner and outer loop. Recovering the phase of the carrier is important otherwise the bit error rate for the data will be compromised.

Fig.11: Basic QAM demodulator

The circuits shown above show the generic IQ QAM modulator and demodulator circuits that are used in a vast number of different areas. Not only are these circuits made from discrete components, but more commonly they are used within integrated circuits that are able to provide a large number of functions.

Key Takeaways:

Error Probability

2. The number of bits necessary to produce a given number of conditions is expressed mathematically as

N=log2M

References:

1. B.P. Lathi, “Modern Digital and Analog communication Systems”, 4th Edition, Oxford University Press, 2010.

2. Rishabh Anand, Communication Systems, Khanna Publishing House, Delhi.

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined