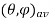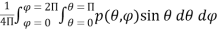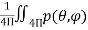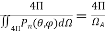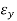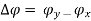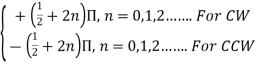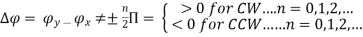Unit-1
Antenna and Fundamental Parameters
An antenna is a device used to transmit and/or receive electromagnetic waves. Electromagnetic waves are often referred to as radio waves. Most antennas are resonant devices, which operate efficiently over a relatively narrow frequency band. An antenna must be tuned (matched) to the same frequency band as the radio system to which it is connected, otherwise reception and/or transmission will be impaired. The device, which converts the required information signal into electromagnetic waves, is known as an Antenna. An Antenna converts electrical power into electromagnetic waves and vice versa.
For wireless communication systems, the antenna is one of the most critical components. A good design of antenna can relax system requirements and improve overall system performance.
The antenna serves to a communication system the same purpose that
eyes and eyeglasses serve to a human
The antenna serves to a communication system the same purpose that
eyes and eyeglasses serve to a human
The antenna serves to a communication system the same purpose that
eyes and eyeglasses serve to a human
The antenna serves to a communication system the same purpose that
eyes and eyeglasses serve to a human
An Antenna can be used either as a transmitting antenna or a receiving antenna.
- A transmitting antenna is one, which converts electrical signals into electromagnetic waves and radiates them.
- A receiving antenna is one, which converts electromagnetic waves from the received beam into electrical signals.
- In two-way communication, the same antenna can be used for both transmission and reception.
Antenna can also be termed as an Aerial. Plural of it is, antennae or antennas. Now-a-days, antennas have undergone many changes, in accordance with their size and shape. There are many types of antennas depending upon their wide variety of applications.
The radiation from the antenna takes place when the Electromagnetic field generated by the source is transmitted to the antenna system through the Transmission line and separated from the Antenna into free space.
1.2.1 Radiation from a Single Wire
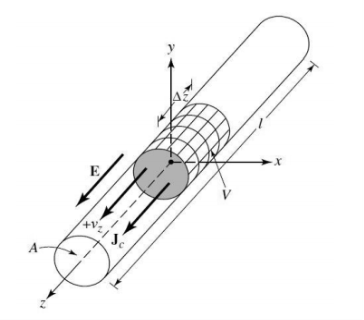
Conducting wires are characterized by the motion of electric charges and the creation of current flow. Assume that an electric volume charge density, qv (coulombs/m3), is distributed uniformly in a circular wire of cross-sectional area A and volume V.
The creation of time-varying electric and magnetic fields between the
conductors forms electromagnetic waves which travel along the transmission
line, as shown in Figure 1.11(a).
The electromagnetic waves enter the antenna and have associated with
them electric charges and corresponding currents. If we remove part of the
antenna structure, as shown in Figure 1.11(b), free-space waves can be
formed by “connecting” the open ends of the electric lines (shown dashed
|
Figure 1.2.1. Charge uniformly distributed in a circular cross section cylinder wire
Current density in a volume with volume charge density qv (C/m3)
Jz = qv vz (A/m2) (1)
Surface current density in a section with a surface charge density qs (C/m2)
For wireless communication systems, the antenna is one of the most critical components. A good design of the antenna can relax system requirements and improve overall system performance
For wireless communication systems, the antenna is one of the most critical components. A good design of the antenna can relax system requirements and improve overall system performance
For wireless communication systems, the antenna is one of the most critical components. A good design of the antenna can relax system requirements and improve overall system performance
For wireless communication systems, the antenna is one of the most critical components. A good design of the antenna can relax system requirements and improve overall system performance
Js = qsvz (A/m) (2)
Current in a thin wire with a linear charge density ql (C/m):
Iz = ql vz (A) (3)
To accelerate/decelerate charges, one needs sources of electromotive force and/or discontinuities of the medium in which the charges move. Such discontinuities can be bends or open ends of wires, change in the electrical properties of the region, etc.
Key takeaway:
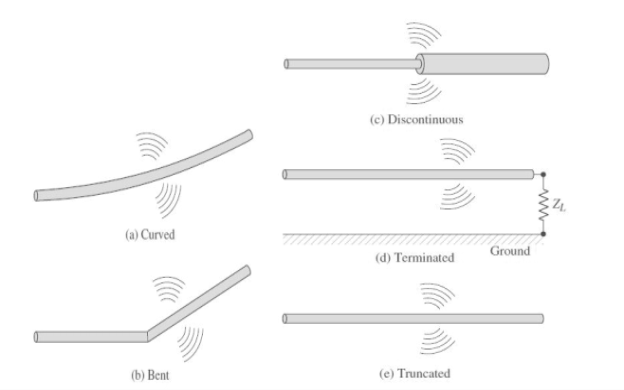
- It is a fundamental single wire antenna. From the principle of radiation there must be some time varying current. For a single wire antenna, If a charge is not moving, current is not created and there is no radiation.
- If charge is moving with a uniform velocity:
a. There is no radiation if the wire is straight, and infinite in extent.
b. There is radiation if the wire is curved, bent, discontinuous, terminated, or truncated, as shown in Figure.
3. If charge is oscillating in a time-motion, it radiates even if the wire is straight.
|
Figure 1.2.1Wire configuration for radiation
1.2.2 Radiation from a Two Wire
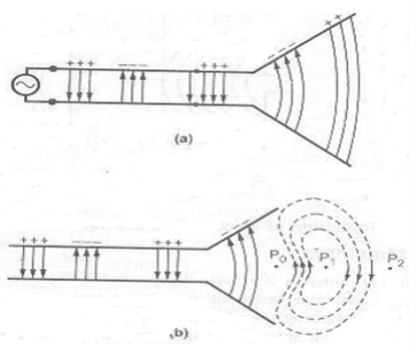
Let us consider a voltage source connected to a two-conductor transmission line which is connected to an antenna. This is shown in Figure (a).
|
Figure 1.2.2: Radiation from two wire antenna
of time-varying electric and magnetic fields between the
conductors forms electromagnetic waves which travel along the transmission
line, as shown in Figure 1.11(a).
The electromagnetic waves enter the antenna and have associated with
them electric charges and corresponding currents. If we remove part of the
antenna structure, as shown in Figure 1.11(b), free-space waves can be
formed by “connecting” the open ends of the electric lines (shown dashed).
of time-varying electric and magnetic fields between the
conductors forms electromagnetic waves which travel along the transmission
line, as shown in Figure 1.11(a).
The electromagnetic waves enter the antenna and have associated with
them electric charges and corresponding currents. If we remove part of the
antenna structure, as shown in Figure 1.11(b), free-space waves can be
formed by “connecting” the open ends of the electric lines (shown dashed).
of time-varying electric and magnetic fields between the
conductors forms electromagnetic waves which travel along the transmission
line, as shown in Figure 1.11(a).
The electromagnetic waves enter the antenna and have associated with
them electric charges and corresponding currents. If we remove part of the
antenna structure, as shown in Figure 1.11(b), free-space waves can be
formed by “connecting” the open ends of the electric lines (shown dashed).
of time-varying electric and magnetic fields between the
conductors forms electromagnetic waves which travel along the transmission
line, as shown in Figure 1.11(a).
The electromagnetic waves enter the antenna and have associated with
them electric charges and corresponding currents. If we remove part of the
antenna structure, as shown in Figure 1.11(b), free-space waves can be
formed by “connecting” the open ends of the electric lines (shown dashed).
- Applying a voltage across the two conductor transmission line creates an electric field between the conductors. The electric field has associated with it electric lines of force which are tangent to the electric field at each point and their strength is proportional to the electric field intensity.
- The electric lines of force have a tendency to act on the free electrons (easily detachable from the atoms) associated with each conductor and force them to be displaced.
- The movement of the charges creates a current that in turn creates magnetic field intensity. Associated with the magnetic field intensity are magnetic lines of force which are tangent to the magnetic field
- . We have accepted that electric field lines start on positive charges and end on negative charges. Magnetic field lines always form closed loops encircling current-carrying conductors because physically there are no magnetic charges.
- The electric field lines drawn between the two conductors help to exhibit the Distribution of charge. If we assume that the voltage source is sinusoidal, we expect the electric field between the conductors to also be sinusoidal with a period equal to that of the applied source. The relative magnitude of the electric field intensity is indicated by the density (bunching) of the lines of force with the arrows showing the relative direction (positive or negative).
Key takeaways:
The radiation from the antenna takes place when the Electromagnetic field generated by the source is transmitted to the antenna system through the Transmission line and separated from the Antenna into free space.
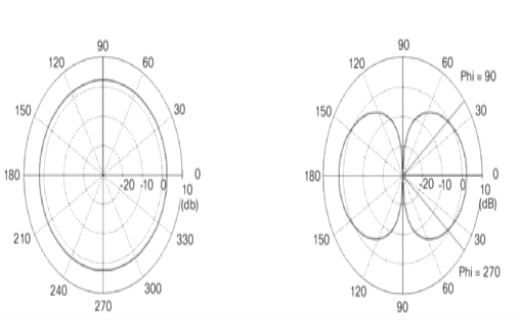
- There are two types of antennas that provide distinct radiating patterns. The first type radiates and receives energy equally in all horizontal directions is called an Omni-Directional Antenna. These antennas are best suited for applications requiring All around coverage.
- An omnidirectional antenna which radiates electromagnetic wave uniformly in a specific plane (often in the azimuth plane) is one of the most popularly used antennas in wireless applications.
- The polarization of the omnidirectional antennas include linear polarizations of vertical polarization and horizontal polarization, dual linear polarization, and circular polarization.
- In addition, the Omni-Directional Antenna’s prominent feature is their pole like radome, such as a monopole. The terms “Rubber Duck” and “Whip Antenna” are commonly used.
- Some examples of Omni-Directional Antennas include our ECO, DOD, OD, PSKN, MOD, Base Stations, hallways, conference rooms, and outside areas etc.
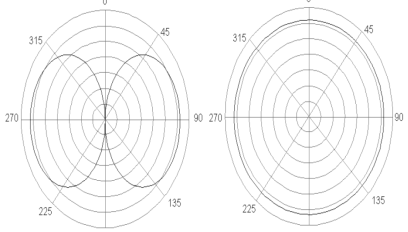
1.3.1. Omnidirectional Antennasradiation pattern
These Omnidirectional antennas have a doughnut shaped radiation pattern and are ideal for connecting devices that are on the same plane and to either side of each other. These are commonly misused in in-building and mobile applications. In mobile applications, Omnidirectional Dipole Antennas fail to have the proper patterning needed in order to connect to a tower that is on a much higher elevation. In in-building applications, Omnidirectional Dipole Antennas fail specifically in point to multipoint deployments where the user can be standing directly underneath a transmitting antenna, and be in a dead zone.
|
Figure1.3.1. Omnidirectional Antennas radiation A pattern
1.3.2.Advantages of Omnidirectional antenna
1. An omnidirectional antenna transmits/receives signals from all directions as in 360 degrees.
1.3.3.Disadvantages of Omnidirectional antenna
1. Signal strength is uniform with omnidirectional antennas.
2. If you use omnidirectional antenna all signals are noise sources look into the same antenna gain.There is neither increase of the desired signal,nor suppression of undesired signals. On a crowded band, the omnidirectional antenna confers no SNR.
Key takeaways:
An omnidirectional antenna which radiates electromagnetic wave uniformly in a specific plane (often in the azimuth plane) is one of the most popularly used antennas in wireless applications.
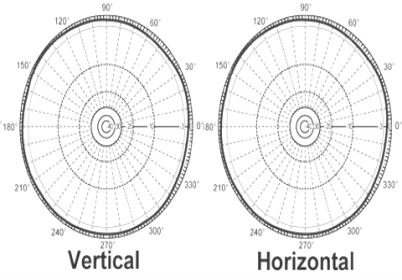
An isotropic antenna is a theoretical antenna that radiates equally in all directions - horizontally and vertically with the same intensity. The antenna has a gain of 1 dB in the spherical space all around it and has an efficiency of 100%. The concept of an isotropic antenna is often used as a reference antenna for the antenna gain.
|
Figure 1.4.Antenna Pattern of an Isotropic Antenna in the Vertical & Horizontal.
1.4.1.Gain
The isotropic radiator has unity gain, which means having a gain factor of 1 in all directions. In terms of dB, it can be called as 0dB gain (zero loss).
Effective Radiated Power
If the radiated power is calculated by taking half-wave dipole as the reference, rather than an isotropic antenna, then it can be termed as ERP (Effective Radiated Power).
ERP(dBW)=EIRP(dBW)−2.15dBi
Key takeaways:
An isotropic antenna is a theoretical antenna that radiates equally in all directions - horizontally and vertically with the same intensity. The antenna has a gain of 1 dB in the spherical space all around it and has an efficiency of 100%.
1.5.1. Antenna pattern
- Definition
The radiation pattern or antenna pattern is the graphical representation of the radiation properties of the antenna as a function of space.
- That is, the antenna's pattern describes how the antenna radiates energy out into space (or how it receives energy).
- It is important to state that an antenna radiates energy in all directions, at least to some extent, so the antenna pattern is actually three-dimensional. It is common, however, to describe this 3D pattern with two planar patterns, called the principal plane patterns.
- These principal plane patterns can be obtained by making two slices through the 3D pattern through the maximum value of the pattern or by direct measurement.
- It is these principal plane patterns that are commonly referred to as the antenna patterns.
|
(a):dipole azimuth radiation pattern (b):dipole elevation radiation pattern
Figure 1.5.1. Antenna patterns
In discussions of principal plane patterns or even antenna patterns, you will frequently encounter the terms azimuth plane pattern and elevation plane pattern. The term azimuth is commonly found in reference to "the horizontal" whereas the term elevation commonly refers to "the vertical".
The fig.(a) shows horizontal pattern and fig.(b) shows vertical pattern.
1.5.2. Half power beam width
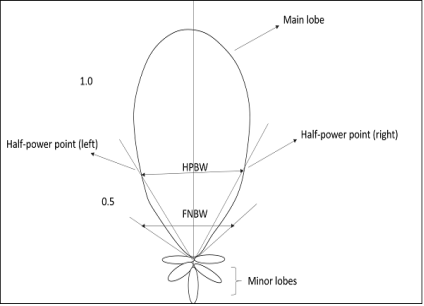
Definition
The 3 dB, or half power, beamwidth of the antenna is defined as the angular width of the radiation pattern, including beam peak maximum, between points 3 dB down from maximum beam level (beam peak).
Indication of HPBW
When a line is drawn between radiation pattern’s origin and the half power points on the major lobe, on both the sides, the angle between those two vectors is termed as HPBW, half power beam width. This can be well understood with the help of the following diagram.
|
Figure 1.5.2 .half-power points on the major lobe and HPBW.
Mathematical Expression
The mathematical expression for half power beam width is
Half power Beam Width = 70 λ /D
Where
- λ is wavelength (λ = 0.3/frequency).
- Dis Diameter.
Units
The unit of HPBW is radians or degrees.
1.5.3.Beam Area (or beam solid angle)
In polar two-dimensional coordinates an incremental area dA on the surface of a sphere is the product of the length r dθ in the θ direction (latitude) and r sin θ dφ in the φ direction (longitude), as shown in Fig. Thus,
dA = (r dθ)(r sinθ dφ) = r 2 dΩ (1)
Where dΩ = solid angle expressed in steradians (sr) or square degrees ( ) dΩ = solid angle subtended by the area dA
The beam area or beam solid angle or ΩA of an antenna is given by the integral of the normalized power pattern over a sphere (4π sr)

1.5.4.Radiation Intensity
- Definition
The power radiated from an antenna per unit solid angle is called the radiation intensity U (watts per steradian or per square degree).
- The normalized power pattern of the previous section can also be expressed in terms of this parameter as the ratio of the radiation intensity U(θ, φ), as a function of angle, to its maximum value. Thus,
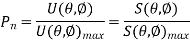
Whereas the Poynting vector S depends on the distance from the antenna (varying inversely as the square of the distance), the radiation intensity U is independent of the distance, assuming in both cases that we are in the far field of the antenna.
1.5.5. Beam Efficiency
- The (total) beam area ΩA (or beam solid angle) consists of the main beam area (or solid angle) ΩM plus the minor-lobe area (or solid angle) Ωm. Thus,
ΩA = ΩM + Ωm
- The ratio of the main beam area to the (total) beam area is called the (main) beam efficiency εM. Thus,
Beam Efficiency =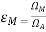 (Dimensionless)
(Dimensionless)
The ratio of the minor-lobe area (Ωm) to the (total) beam area is called the stray factor. Thus
 = stray factor
= stray factor
It follows that
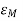 +
+  = 1
= 1
1.5.6. Directivity (D) AND Gain (G)
1.5.6.1. Directivity (D)
The directivity D and the gain G are probably the most important parameters of an antenna. The directivity of an antenna is equal to the ratio of the maximum power density P(θ, φ)max (watts/m2 ) to its average value over a sphere as observed in the far field of an antenna. Thus,
D = 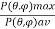
The directivity is a dimensionless ratio ≥1. The average power density over a sphere is given by
P = Therefore, the directivity D =
And D = |
This is the diversity from beam area,where Pn(θ, φ) dΩ = P(θ, φ)/P(θ, φ)max = normalized power pattern.
1.5.6.2. Gain
The gain G of an antenna is an actual or realized quantity which is less than the directivity D due to ohmic losses in the antenna or its radome (if it is enclosed). In transmitting, these losses involve power fed to the antenna which is not radiated but heats the antenna structure. A mismatch in feeding the antenna can also reduce the gain. The ratio of the gain to the directivity is the antenna efficiency factor. Thus, G = kD
Where k= Efficiency factor (0< k< 1), dimensionless
1.5.7 Resolution
- Definition
The resolution of an antenna may be defined as equal to half the beam width between first nulls (FNBW)/2.
- When the antenna beam maximum is aligned with one satellite, the first null coincides with the adjacent satellite. Half the beamwidth between first nulls is approximately equal to the half-power beamwidth (HPBW) or
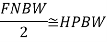
- The product of the FNBW/2 in the two principal planes of the antenna pattern is a measure of the antenna beam area. Thus,

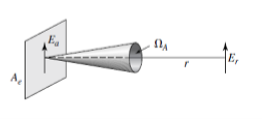
1.5.8. Antenna Apertures
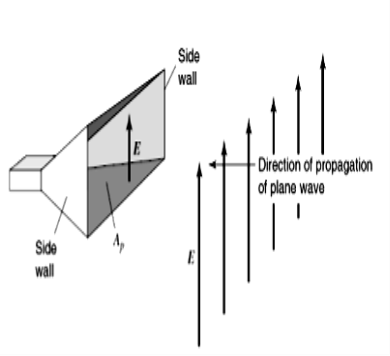
- The concept of aperture is most simply introduced by considering a receiving antenna. Suppose that the receiving antenna is a rectangular electromagnetic horn immersed in the field of a uniform plane wave as suggested in Fig.
- Let the Poynting vector, or power density, of the plane wave be S watts per square meter and the area, or physical aperture of the horn, be Ap square meters. If the horn extracts all the power from the wave over its entire physical aperture, then the total power P absorbed from the wave is
|
Figure 1.5 8.Plane wave incident on electromagnetic horn of physical aperture AP
P = 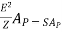
|
Figure 1.5 8. Radiation over beam area
- Thus, the electromagnetic horn may be regarded as having an aperture, the total power it extracts from a passing wave being proportional to the aperture or area of its mouth. But the field response of the horn is NOT uniform across the aperture A because E at the sidewalls must equal zero.
- Thus, the effective aperture Ae of the horn is less than the physical aperture Ap as given by
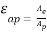 (Dimensionless) Aperture efficiency
(Dimensionless) Aperture efficiency
where εap =aperture efficiency.
1.5.9. Effective height
- The effective height h (meters) of an antenna is another parameter related to the aperture. multiplying the effective height by the incident field E (volts per meter) of the same polarization gives the voltage V induced.
- Thus, V = hE (1) Accordingly, the effective height may be defined as the ratio of the induced voltage to the incident field or h = V/E (m)
1.5.10. Radiation Resistance
- It is that part of an antenna's feedpoint electrical resistance that is caused by the radiation of electromagnetic waves from the antenna.
- The radiation resistance RR can be defined as the value of resistance that would dissipate the same amount of power as radiated as radio waves by the antenna with the antenna input current passing through it.
- It is equal to the total power PR radiated as radio waves by the antenna divided by the square of the rms current Irms into the antenna terminals:
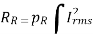
- The radiation resistance is determined by the geometry of the antenna and the operating frequency.
1.5.11.Front to back ratio
- The Front to Back Ratio (F/B Ratio) of an antenna is the ratio of power radiated in the front/main radiation lobe and the power radiated in the opposite direction (180 degrees from the main beam)
.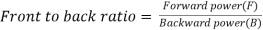
- This ratio tells us the extent of backward radiation and is normally expressed in dB. This parameter is important in circumstances where interference or coverage in the reverse direction needs to be minimized
1.5.12. Reflection coefficient
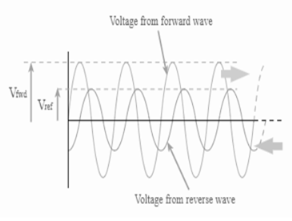
In the context of antennas and feeders, the reflection coefficient is defined as the figure that quantifies how much of an electromagnetic wave is reflected by an impedance discontinuity in the transmission medium. The reflection coefficient is equal to the ratio of the amplitude of the reflected wave to the incident wave.
Calculating reflection coefficient
- There are many ways in which the reflection coefficient can be calculated.
- Using the basic definition of the reflection coefficient, it can be calculated from a knowledge of the incident and reflected voltages.
|
Figure 1.5.12. Reflection coefficient
r = 
Where,
r= reflection co-efficient
Vref= = reflected voltage
Vfwd = forward voltage
- It is also useful to be able to calculate the reflection coefficient in terms of the forward and reverse power levels. As the power is proportional to V2 [ watts = V2 / R], we can deduce that:
r = 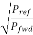
Where:
Γ = reflection coefficient
Pref = reflected power
Pfwd = forward power
1.5.13. Impedence bandwidth
- The "impedance bandwidth" is just the ordinary bandwidth of the antenna. Normally this is defined as the range of frequencies over which the return loss is acceptable.
- Bandwidth of an antenna is an important concept. The bandwidth of an antenna refers to the range of frequencies over which the antenna satisfies a particular parameter specification.
- The parameters generally specified are gain, radiation pattern, the VSWR etc. Most commonly, the VSWR is chosen as the parameter for bandwidth considerations and this bandwidth is called the impedance bandwidth.
1.5.14.Pattern bandwidth
Bandwidth can be defined in terms of radiation patterns or VSWR/reflected power. The definition used is based on VSWR. Bandwidth is often expressed in terms of percent bandwidth, because the percent bandwidth is constant relative to frequency.
1.5.15. Polarization of an antenna
- When the direction is not stated, the polarization is taken to be the polarization in the direction of maximum gain.‖ In practice, polarization of the radiated energy varies with the direction from the center of the antenna, so that different parts of the pattern may have different polarizations
- Polarization may be classified as linear, circular, or elliptical.
- If the vector that describes the electric field at a point in space as a function of time is always directed along a line, the field is said to be linearly polarized.
- In general, however, the electric field traces is an ellipse, and the field is said to be elliptically polarized.
- Linear and circular polarizations are special cases of elliptical, and they can be obtained when the ellipse becomes a straight line or a circle, respectively.
- The electric field is traced in a clockwise (CW) or counterclockwise (CCW) sense. Clockwise rotation of the electric-field vector is also designated as right-hand polarization and counterclockwise as left-hand polarization.
- Linear Polarization For the wave to have linear polarization, the time-phase difference between the two components must be
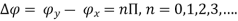
- Circular Polarization Circular polarization can be achieved only when the magnitudes of the two components are the same and the time-phase difference between them is odd multiples of π/2.
|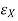 |=|
|=|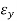 |
|
 =
= 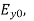
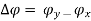 =
= 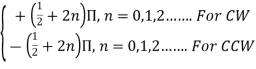
- Elliptical Polarization Elliptical polarization can be attained only when the time-phase difference between the two components is odd multiples of π/2 and their magnitudes are not the same or when the timephase difference between the two components is not equal to multiples of π/2 (irrespective of their magnitudes). That is
|
1.5.16.Antenna Field Zones
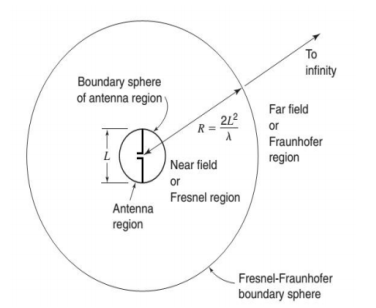
- The fields around an antenna may be divided into two principal regions, one near the antenna called the near field or Fresnel zone and one at a large distance called the far field or Fraunhofer zone.
- The boundary between the two may be arbitrarily taken to be at a radius
R = 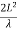 (m)
(m)
where
L= Maximum dimension of the antenna in meters
λ=wavelength, meters
In the far or Fraunhofer region, the measurable field components are transverse to the radial direction from the antenna and all power flow is directed radially outward. In the far field the shape of the field pattern is independent of the distance. In the near or Fresnel region, the longitudinal component of the electric field may be significant and power flow is not entirely radial. In the near field, the shape of the field pattern depends, in general, on the distance.
|
Figure 1.5.16. Antenna region, Fresnel region and Fraunhofer region.
1.5.17 Antenna Temperature
- It is a measure of the noise being produced by an antenna in a given environment. This is also called an Antenna Noise Temperature.
- It is not the physical temperature of the antenna. This temperature depends of the gain, radiation pattern and the noise that the antenna picks up from the surrounding environment.
- The Antenna Temperature can be represented by the following formula:
 temperature (
temperature (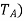 =
=
- This equation shows that the antenna temperature is calculated by integrating over the entire sphere, based on the radiation pattern of the antenna and the temperature distribution of the antenna.
R(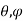 ) is the radiation pattern of the antenna.
) is the radiation pattern of the antenna.
T( )is temperature distribution of the antenna based on its surroundings. For example, the temperature of the night sky is 4 Kelvin, the value of the temperature pattern in the direction of the ground would be based on the physical temperature of the ground.
)is temperature distribution of the antenna based on its surroundings. For example, the temperature of the night sky is 4 Kelvin, the value of the temperature pattern in the direction of the ground would be based on the physical temperature of the ground.
Key takeaways :
2. The radiation pattern or antenna pattern is the graphical representation of the radiation properties of the antenna as a function of space.
3. Beam width of the antenna is defined as the angular width of the radiation pattern, including beam peak maximum, between points 3 dB down from maximum beam level (beam peak).
4. The beam area or beam solid angle or ΩA of an antenna is given by the integral of the normalized power pattern over a sphere (4π sr)
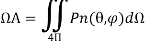
5. The power radiated from an antenna per unit solid angle is called the radiation intensity U (watts per steradian or per square degree).
6. The ratio of the main beam area to the (total) beam area is called the (main) beam efficiency εM. Thus,
Beam Efficiency =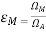 (Dimensionless)
(Dimensionless)
7. The directivity of an antenna is equal to the ratio of the maximum power density P (θ, φ)max (watts/m2 ) to its average value over a sphere as observed in the far field of an antenna. Thus,
D = 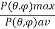
8. The resolution of an antenna may be defined as equal to half the beam width between first nulls (FNBW)/2.
9. The effective height h (meters) of an antenna is another parameter related to the aperture. multiplying the effective height by the incident field E (volts per meter) of the same polarization gives the voltage V induced.
10. The radiation resistance RR can be defined as the value of resistance that would dissipate the same amount of power as radiated as radio waves by the antenna with the antenna input current passing through it.
11. The Front to Back Ratio (F/B Ratio) of an antenna is the ratio of power radiated in the front/main radiation lobe and the power radiated in the opposite direction (180 degrees from the main beam)
.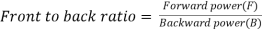
12. The reflection coefficient is equal to the ratio of the amplitude of the reflected wave to the incident wave.
13. Impedance Bandwidth is defined as the range of frequencies over which the return loss is acceptable.
14. If the vector that describes the electric field at a point in space as a function of time is always directed along a line, the field is said to be linearly polarized.
15. In general, however, the electric field traces is an ellipse, and the field is said to be elliptically polarized.)
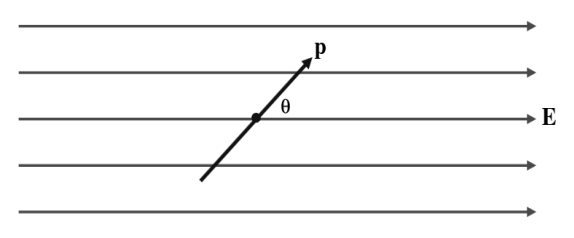
16. Consider a dipole oscillating in an electric field, When it is at an angle θ to the field, the magnitude of the restoring torque on it is pEsinθ, and therefore its equation of motion is
Iθ¨=−pEsinθ
where I is its rotational inertia.
|
Figure 1.6 Electric field from oscillating dipole
17. For small angles, Equation above can be approximated as
Iθ¨≈−pEθ
18. The period of small oscillations is
P = 2
Key takeaways :
- The equation of motion of dipole in electric field is Iθ¨≈−pEθ)
19. The Friis transmission formula is used in telecommunications engineering, equating the power at the terminals of a receive antenna as the product of power density of the incident wave and the effective aperture of the receiving antenna under idealized conditions given another antenna some distance away transmitting a known amount of power

Pr = Received power, W
Pt = Received power, W
Aet = Effective aperture of transmitting antenna, m2
Aer = Effective aperture of receiving antenna, m2
r = Distance between antennas, m
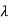 = Wavelength, m
= Wavelength, m
Key takeaways :
20. The Friis transmission formula is used in telecommunications engineering, equating the power at the terminals of a receive antenna as the product of power density of the incident wave and the effective aperture of the receiving antenna under idealized conditions given another antenna some distance away transmitting a known amount of power.
21. Friss transmission is given by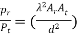 )
)
References
- “Antenna and Wave Propagation” by Sisir Das and Annapurna Das.
- “Antennas and Wave Propagation” by Soundararajan.
- “Antennas and Wave Propagation” by A R Harish and M Sachidananda.