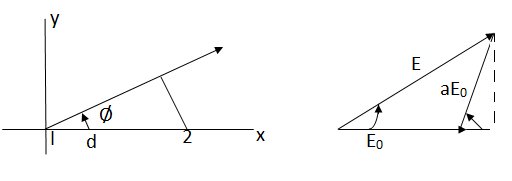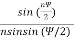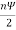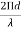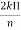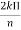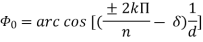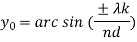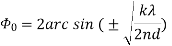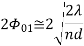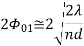Unit-2
Antenna Arrays
● Antennas with a given radiation pattern may be arranged in a pattern line, circle, plane, etc.) to yield a different radiation pattern.
● Antenna array - a configuration of multiple antennas (elements) arranged to achieve a given radiation pattern. Simple antennas can be combined to achieve desired directional effects. Individual antennas are called elements and the combination is an array.
2.1.1. Types of Arrays
● Linear array - antenna elements arranged along a straight line.
● Circular array - antenna elements arranged around a circular ring.
● Planar array - antenna elements arranged over some planar surface (example - rectangular array).
● Conformal array - antenna elements arranged to conform two some non-planar surface (such as an aircraft skin).
2.1.2. Design Principles of Arrays
There are several array design variables which can be changed to achieve the overall array pattern design.
● General array shape (linear, circular, planar)
● Element spacing.
● Element excitation amplitude.
● Element excitation phase.
● Patterns of array elements.
2.1.3. Application of Arrays
● An array of antennas may be used in a variety of ways to improve the performance of a communications system. Perhaps most important is its capability to cancel co channel interferences.
● An array works on the premise that the desired signal and unwanted co channel interferences arrive from different directions.
● The beam pattern of the array is adjusted to suit the requirements by combining signals from different antennas with appropriate weighting.
● An array of antennas mounted on vehicles, ships, aircraft, satellites, and base stations is expected to play an important role in fulfilling the increased demand of channel requirement for these services.
ARRAY is an assembly of antennas in an electrical and geometrical of such a nature that the radiation from each element add up to give a maximum field intensity in a particular direction& cancels in other directions. An important characteristic of an array is the change of its radiation pattern in response to different excitations of its antenna elements.
2.2.1. Isotropic point sources of same amplitude and phase
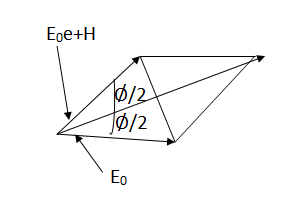
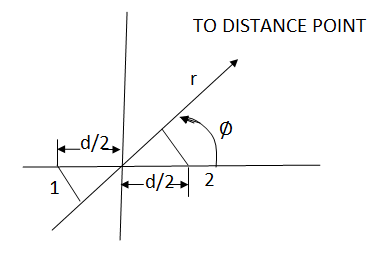
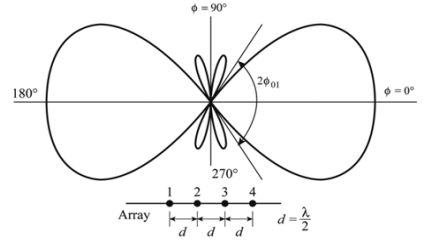
● Two point sources 1 and 2 are seperated by d & located symmetrically with respect to the origin.
● The origin of the co-ordinates is taken as the reference for the phase.
● In the direction of φ, the fields from sources 1 and 2 are retarded and advanced respectively by 
d,cosφ
Where, d=
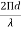=kd
|
Figure 2.2.1.1. Isotropic point sources of same amplitude and phase
|
Figure 2.2.1.2. Vector addition
|
Figure 2.2.1.3. Phase of total field
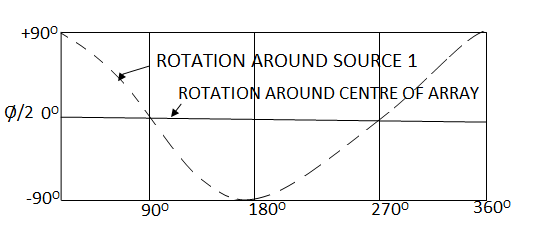
● This figure shows the phase of total field as afunction of φ for two isotropic point sources of same amplitude and phase spaced 
apart.The phase change is zero when refferd to the centre point of the array but is 
as shown by the dashed curve when referred to source 1.
|
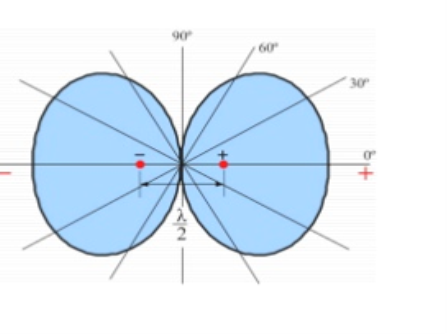
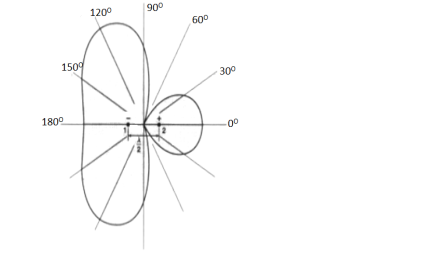
Figure 2.2.1.4. Isotropic point sources pattern of same amplitude and phase
● Total field at a distance r in φ direction is
E=E0 e-jΨ/2 + E0 e +jΨ/2
Where Ψ(φ)= kd cos(φ)
E= 2 E0 cos
E= 2 E0 cos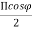
|E|= cos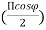
● Field from source in φ direction is advanced by Ψ =d, cosφ
Where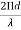, d=
=kd
E=E0 e +jΨ = E=E0 e +jΨ/2( e-jΨ/2 + +jΨ/2)
E= 2 E0 cos
2.2.2. Isotropic point sources of same amplitude and opposite phase
Consider the same case except that two sources are in opposite phase.
|
2.2.2. Isotropic point sources pattern of same amplitude and opposite phase
E=-E0 e-jΨ/2 + E0 e +jΨ/2
E= 2j E0 sin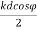
|E|= sin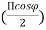
Ex. E= sin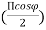 
2.2.3. Isotropic point sources of same amplitude and in phase quadrature
Let sorces 1 and 2 be retarded and advanced respectively, both by 
|
|
Fig.2.2.3.1. Isotropic point sources pattern of same amplitude and in phase quadrature for spacing 
.
● This figure shows thefield pattern of two isotropic point sources of same amplitude and in phase quadrature for a spacing of
. The source to the right leads that to the left by 900.
|
2.2.3.2. Isotropic point sources pattern of same amplitude and in phase quadrature for spacing
.
● This figure shows the field pattern of two isotropic point sources of same amplitude and in phase quadrature for a spacing of 
. The source 2 leads source 1by 900.
E=E0 e-j(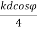
) + E0 e+j(
)
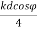=2E0 COS ((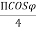
)+
)
|E|= cos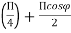
2.2.4. Isotropic point sources of same amplitude and any phase difference
● Two point sources 1 and 2 are seperated by d having same amplitude.
● The origin of the co-ordinates is taken as the reference for the phase.
● Total phase difference Ψ between fields from sources 2 & 1 in φ direction.
|
Fig 2.2.4. Isotropic point sources of same amplitude and any phase difference
E=E0 e-jΨ/2 + E0 e +jΨ/2
E= 2 E0 cos
E= cos
2.2.5. Isotropic point sources of unequal amplitude and any phase difference
Assume that source 1 has larger field amplitude, which is E0 at a distance r.
|
Figure.2.2.5. Isotropic point sources of unequal amplitude and any phase difference
E=E0
.
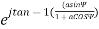
Where,Ψ=d
Key takeaways :
● ARRAY is an assembly of antennas in an electrical and geometrical of such a nature that the radiation from each element add up to give a maximum field intensity in a particular direction & cancels in other directions.
● An important characteristic of an array is the change of its radiation pattern in response to different excitations of its antenna elements.
● The phase change is zero when refferd to the centre point of the array.)
2.3.1. Non-isotropic But similar point sources
● Field pattern of an array of similar non isotropic point sources is equal to the addition of phase pattern of individual array and phase pattern of an array of isotropic sources with same location, relative amplitude and phase.
1. Applied to arrays of any number of similar sources.
2. For field magnitude only.
● Phase pattern of an array of similar non isotropic point sources is equal to the addition of phase pattern of individual source and phase pattern of an array of isotropic sources with same location, relative amplitude and phase.
● Thus, total field E is
E = f (θ,φ) f(θ,φ)ej|f((θ,φ))+f((θ,φ)|
|
Figure 2.3.1.Non-isotropic But similar point sources pattern
2.3.2. Pattern multiplication
● Principle of pattern multiplication
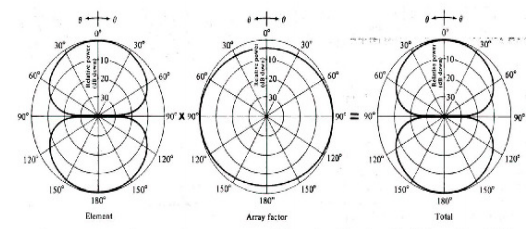
The total far-field radiation pattern |E| of array (array pattern) consists of the original radiation pattern of a single array element multiplying with the magnitude of the array factor |AF|. This is a general property of antenna arrays and is called the principle of pattern multiplication.
|
Figure 2.3.2. Array pattern of two-element arrays
Key takeaways:
● Field pattern of an array of similar non isotropic point sources is equal to the addition of phase pattern of individual array and phase pattern of an array of isotropic sources with same location, relative amplitude and phase.
● The total far-field radiation pattern |E| of array (array pattern) consists of the original radiation pattern of a single array element multiplying with the magnitude of the array factor |AF|.
● This is a general property of antenna arrays and is called the principle of pattern multiplication.)
● Field pattern of an array of dissimilar non isotropic point sources is not equal to the addition of phase pattern of individual array and phase pattern of an array of isotropic sources with same location, relative amplitude and phase.
● Uniform array has identical elements, identical magnitude, progressive phase and also uniform spacing.
● At higher frequencies, for point to point communications it is necessary to have a pattern with single beam radiation. Such highly directive single beam pattern can be obtained by increasing the point sources in the arrow from 2 to n say.
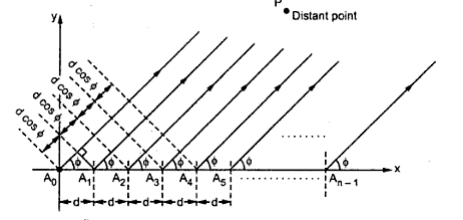
● An array of n elements is said to be linear array if all the individual elements are spaced equally along a line. An array is said to be uniform array if the elements in the array are fed with currents with equal magnitudes and with uniform progressive phase shift along the line.
● Consider a general n element linear and uniform array with all the individual elements spaced equally at distance d from each other and all elements are fed with currents equal in magnitude and uniform progressive phase shift along line as shown in the Fig.
|
Figure 2.5. Linear arrays of n isotropic point source of equal amplitude and spacing
E TOTAL = E1 + E2 +…….+ EN
|
Key takeaways:
Uniform array has identical elements, identical magnitude, progressive phase and also uniform spacing.)
Enorm = For finding direction of Nulls: Sin ( For broadside array:
2. For Broadside, Null direction array length,
And beamwidth between first nulls(long array)
3. For Ordinary end fire, Null direction array length,
And beamwidth between first nulls(long array)
4. For End fire with increased directivity
5. And beam width between first nulls(long array)
|
|
Figure 2.6. First null beam width
The broadside array is defined as “the radiation pattern's direction is perpendicular or broadside to the array axis”.
It uses the dipole elements that are fed in phase and separated by the one-half wave length. A broadside array is a type of antenna array which is used to radiate the energy in specific direction to make better transmission. It is a bidirectional array which can send and receive process at both ends (sending and receiving end).
The front view of the broadside array is shown below.
|
Figure 2.7. Broadside Array
From this Figure 1, the broadside array is at extreme right angle direction to the array plane. However, due to pattern cancellation in the path joining at the center, the radiation pattern is too less.
Radiation pattern
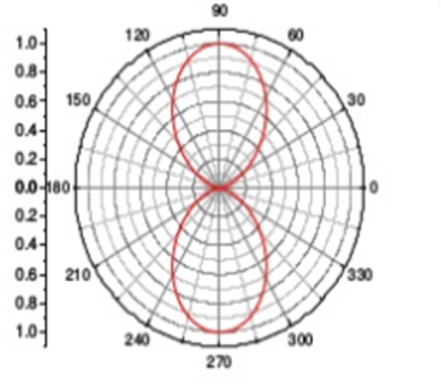
There are different types antenna array present. Each have their own radiation pattern. The broadside array's pattern is drawn and shown below.
|
Figure 2. 7.1. Radiation patter
This pattern is at right angles to the plane and is bi-directional. The radiation beam has very narrow pattern and has high gain.
Write the formula to find Etotal in the plane.
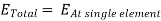* AF
Here, Array factor is denoted by AF, Total radiation pattern is denoted as Etotal and The radiation pattern at single element is denoted as Eat single element.
Write the series to find array factor in n-element.
AF =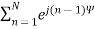 
Here, Relative phase is denoted by ψ.
Write expression to find relative phase.
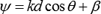
Here, The array element distance is denoted as d, Constant parameter is denoted as k, Path is denoted as β, and Angle calculated from the z-axis is denoted as θ.
Key takeaways :
● The broadside array is defined as “the radiation pattern's direction is perpendicular or broadside to the array axis”.
● Its pattern is at right angles to the plane and is bi-directional. The radiation beam has very narrow pattern and has high gain.)
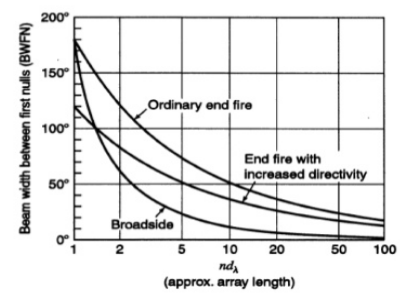
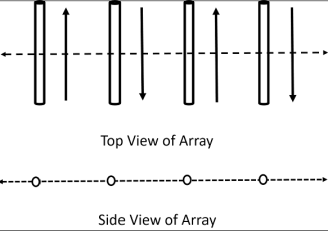
The physical arrangement of end-fire array is same as that of the broad side array. The magnitude of currents in each element is same, but there is a phase difference between these currents. This induction of energy differs in each element, which can be understood by the following diagram.
|
Figure 2.8.1. End- fire array
The above figure shows the end-fire array in top and side views respectively.
There is no radiation in the right angles to the plane of the array because of cancellation. The first and third elements are fed out of phase and therefore cancel each other’s radiation. Similarly, second and fourth are fed out of phase, to get cancelled.
The usual dipole spacing will be λ/4 or 3λ/4. This arrangement not only helps to avoid the radiation perpendicular to the antenna plane, but also helps the radiated energy get diverted to the direction of radiation of the whole array. Hence, the minor lobes are avoided and the directivity is increased. The beam becomes narrower with the increased elements.
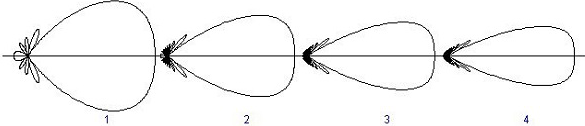
The Radiation pattern of end-fire array is uni-directional. A major lobe occurs at one end, where maximum radiation is present, while the minor lobes represent the losses.
|
Figure 2.8.2.Radiation pattern
The figure explains the radiation pattern of an end-fire array. Figure 1 is the radiation pattern for a single array, while figures 2, 3, and 4 represent the radiation pattern for multiple arrays.
Key takeaways:
● The physical arrangement of end-fire array is same as that of the broad side array.
● The magnitude of currents in each element is same, but there is a phase difference between these currents.
● The Radiation pattern of end-fire array is uni-directional. A major lobe occurs at one end, where maximum radiation is present, while the minor lobes represent the losses.)
References
|
|
