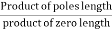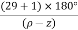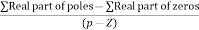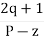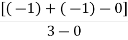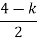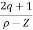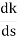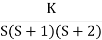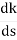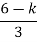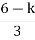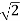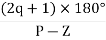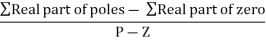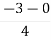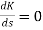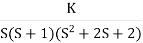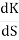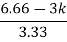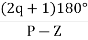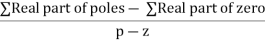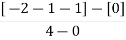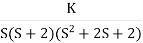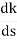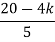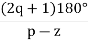UNIT - 4
Root Locus Techniques
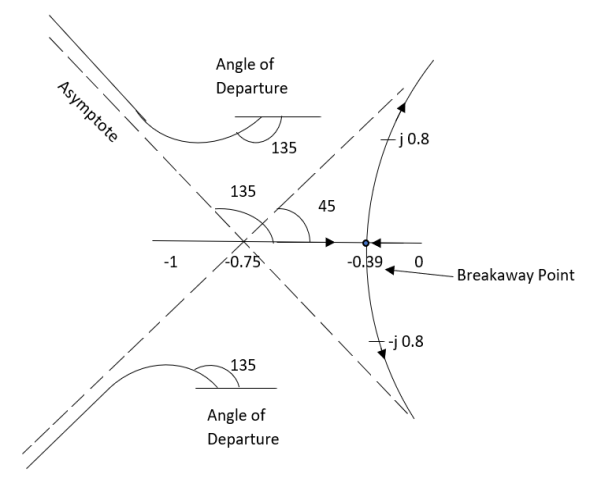
The root locus is a graphical produce for determining the stability of a control system which is determined by the location of the poles. The poles are nothing but the roots of the characteristic equation.
- It is symmetrical to the real axis.
- Number of branches of root locus is equal to number of max (poles or zero).
- Starting point (k=0) End point(k—>∞)
(open loop poles) (open loop zeros)
- A point on the real axis lies on the root locus if number of open loop poles or zero to the right side of that point is odd in number.
- Value of K anywhere on the root locus is given as
K = |
I) If poles > zeros, then (Þ-z) branches will terminate at ∞ (where k=∞)
II) If Z > P, then (Z-P) branches will start from ∞ (K = 0)
- When P>Z, (P-Z) branches will terminate at ∞ (open loop zeros). But by which path. So the path is shown by asymptotes and this asymptotes is given by
Asymptote = |
- There asymptotes intersect the real axis at a single point and this point is known as centroid.
Centroid = |
- Break away and break in point when root locus lies between two poles its called break in point.
Differentials the characteristic equation and equate to zero 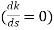
- Angle of arrival and angle of departure this print is used when the roots are complex.
Angle of departure - for complex poles
Angle of arrival – for complex zero.
 øD =(2q+1) 180° + ø
øD =(2q+1) 180° + ø
øA = (2q+1) 180° - ø ø = ∠Z– ∠P.
- Intersection of root locus with imaginary axis can be calculated by Routh Hurwitz. By calculating valve of k at intersection point (we can comment about system stability) so by knowing values of k at intersection point (imaginary axis) the valve of s at that point can also be calculated.
Key takeaways
Centroid and Breakaway points are not same
Examples
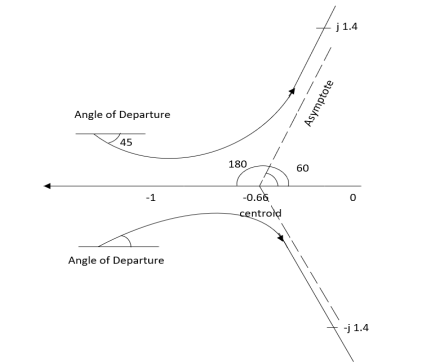
Q1. Sketch the root locus for given open loop transfer function G(S) = 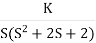 .
.
Soln:- 1) G(s) = 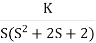
Number of Zeros = 0
Number of polls S = (0, -1+j, -1-j) = (3).
- Number of Branches = max (P, Z) = max (3, 0) = 3.
- As there are no zeros in the system so, all branches terminate at infinity.
- As P>Z, branches terminate at infinity through the path shown by asymptotes
Asymptote = P=3, Z=0. q= 0, 1, 2. For q=0 Asymptote = 1/3 × 180° = 60° For q=1 Asymptote = = 180° For q=2 Asymptote = Asymptotes = 60°,180°,300°.
Centroid = = Centroid = -0.66 |
- As poles are complex so angle of departure
øD = (2q+1)×180°+ø
ø = ∠Z –∠P.
Calculating ø for S=0
|
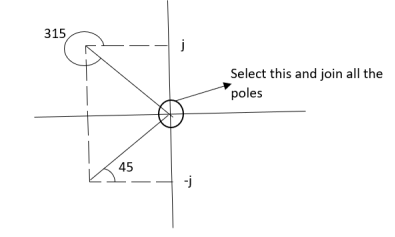
Join all the other poles with S=0
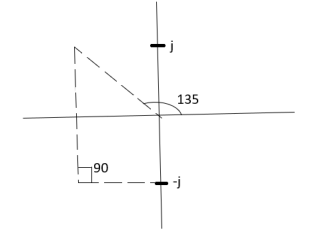
ø = ∠Z –∠P. = 0-(315°+45°) = -360° ØD = (2q + 1)180 + ø. = 180° - 360° ØD = -180° (for q=0) = 180° (for q=1) =540° (for q=2) |
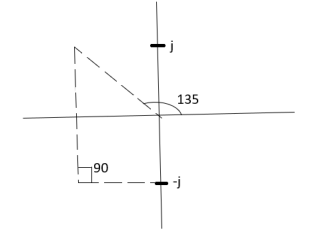
Calculation ØD for pole at (-1+j)
|
ø = ∠Z –∠P.
= 0 –(135°+90°)
= -225°
ØD = (2q+1) 180°+ø.
= 180-225°
= -45°
ØD = -45° (for q = 0)
= 315° (for q = 1)
= 675° (for q =2)
- The crossing point on imaginary axis can be calculated by Routh Hurwitz the characteristic equation is.
1+G(s) H (s) = 0
1+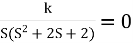
S (S2+2s+2)+k = 0
S3+2s2+2s+K = 0

S3 | 1 | 1 | 0 |
S2 | 2 | K | 0 |
S1 |
| 0 |
|
S0 | K |
|
|
The root locus plot is shown in figure 1.
|
Fig 1 Root Locus For G(S) = 
Q2. Sketch the root locus plot for the following open loop transfer function
G(s) = 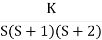
- Number of zero = 0, number of poles = 3
- As P>Z, branches will terminates at infinity
- There are no zeros so all branches will terminate at infinity.
- The path for the branches is shown by asymptote
Asymptote = P=3, Z=0 q= 0,1,2. For q = 0 Asymptote = For q=1 Asymptote = For q=2 Asymptote =
Centroid = =
So, calculating breakaway point.
The characteristic equation is 1+ G(s) H (s) = 0. 1+ K = -(S3+3S2+2s)
3s2+6s+2 = 0 S = -0.423, -1.577. So, breakaway point is at S=-0.423 because root locus is between S= 0 and S= -1
Characteristics equation is S3+3S3+2s+K = 0 |
| 1 | 2 |
S2 | 3 | K |
S1 |
| 0 |
S0 | K |
|
For k Sn-1= 0 n: no. of intersection with imaginary axis n=2 S1 = 0 K < 6 Valve of S at the above valve of K Sn = 0 S2 = 0 3S2 + K =0 3S2 +6 = 0 S2 + 2 = 0 S = ± |
|
Fig 2 Root Locus For G(s) = 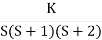
The root locus plot is shown in fig. 2.
Q3. Plot the root locus for the given open loop transfer function
G(s) = 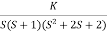
- Number of zeros = 0 number of poles = 4
P = (S=0,-1,-1+j,-1-j) = 4
- As P>Z all the branches will terminated at infinity.
- As no zeros so all branches terminate at infinity.
- The path for branches is shown by asymptote.
Asymptote = q=0,1,2,3. (P-Z = 4-0) for q=0 Asymptote = For q=1 Asymptote = For q=2 Asymptote = For q=3 Asymptote =
Centroid =
Centroid = 6) As poles are complex so angle of departure is
ØD = (2q+1) ×180 + ø ø = ∠Z –∠P.
A) Calculating Ø for S=0 | |
| |
ø = ∠Z –∠P. = 0 –[315° + 45°] Ø = -360° For q = 0 ØD = (2q+1) 180° + Ø = 180 - 360° ØD = -180° b) Calculating Ø for S=-1+j ø = ∠Z –∠P. = 0-[135° + 90° + 90°] Ø = -315° For q=0 ØD= (2q+1) 180° +Ø = 180° -315° ØD = -135° ØD for S=1+j will be ØD = 45° 6) As the root locus lie between S=0 and S=-1 So, the breakaway point is calculated
1+ G(s)H(s) = 0
1+
(S2+S)(S2 +2S+2) + K =0 K = -[S4+S3+2s3+2s2+2s2+2s]
S = -0.39, -0.93, -0.93.
| |
The breakaway point is at S = -0.39 as root locus exists between S= 0 and S=-1
7) Intersection of root locus with imaginary axis is given by Routh Hurwitz
I + G(s) H(s) = 0
For system to be stable
6.66>3K 0<K<2.22. For K = 2.22 3.3352+K =0 3.3352 + 2.22 = 0 S2 = -0.66 S = ± j 0.816. The root locus plot is shown in figure 3. | ||||||||||||||||||||
|
Fig-3 Root Locus For G(s) = 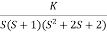
Q4. Plot the root locus for open loop system
G(s) = 
- Number of zero = 0 number of poles = 4 located at S=0, -2, -1+j, -1-j.
- As no zeros are present so all branches terminated at infinity.
- As P>Z, the path for branches is shown by asymptote
Asymptote = q = 0,1,2……p-z-1 For q = 0 Asymptote = 45° q=1 Asymptote = 135° q=2 Asymptote = 225° q=3 Asymptote = 315°
Centroid = = Centroid = -1.
ØD=(2q+1)180° + Ø ø = ∠Z –∠P = 0-[135°+45°+90°] = 180°- 270° ØD = -90°
1+ G(s)H(s) = 0
1+
K = -[S4+2S3+2S2+2S3+4S2+4S] K = -[S4+4S3+6S2+4S]
S = -1 So, breakaway point is at S = -1
K≤5. For K=5 valve of S will be. 5S2+K = 0 5S2+5 = 0 S2 +1 = 0 S2 = -1 S = ±j. The root locus is shown in figure 4. | ||||||||||||||||||||
|
Fig-4 Root Locus for G(s) = 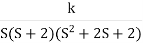
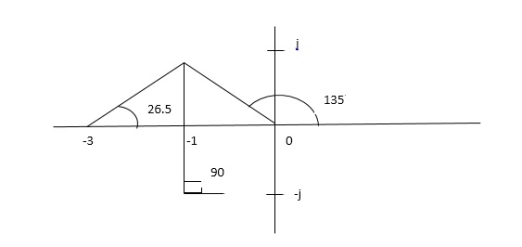
Q5. Plot the root locus for open loop transfer function G(s) = 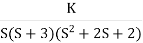
- Number of zeros = 0. Number of poles = 4 located at S=0, -3, -1+j, -1-j.
- As no. zero so all branches terminate at infinity.
- The asymptote shows the both to the branches terminating at infinity.
Asymptote = For q = 0 Asymptote = 45 For q = 1 Asymptote = 135 For q = 2 Asymptote = 225 For q = 3 Asymptote = 315 (4). The asymptote intersects real axis at centroid. Centroid = ∑Real part of poles - ∑Real part of zero / P – Z = [-3-1-1] – 0 / 4 – 0 Centroid = -1.25 (5). As poles are complex so angle of departure φD = (29 + 1)180 + φ |
|
ø = ∠Z –∠P. = 0 – [ 135 + 26.5 + 90 ] = -251.56 For q = 0 φD = (29 + 1)180 + φ = 180 – 215.5 φD = - 71.56
(6). Break away point dk / ds = 0 is at S = -2.28.
(7). The intersection of root locus on imaginary axis is given by Routh Hurwitz. 1 + G(S)H(S) = 0 K + S4 + 3S3 + 2S3 + 6S2 + 2S2 + 6S = 0 S4 1 8 K S3 5 6 S2 34/5 K S1 40.8 – 5K/6.8 K ≤ 8.16 For K = 8.16 value of S will be 6.8 S2 + K = 0 6.8 S2 + 8.16 = 0 S2 = - 1.2 S = ± j1.09 |
The plot is shown in figure 5[11]. |
|
Fig-5 Root Locus for G(s) = 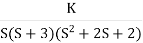
Q.6. Sketch the root locus for open loop transfer function.
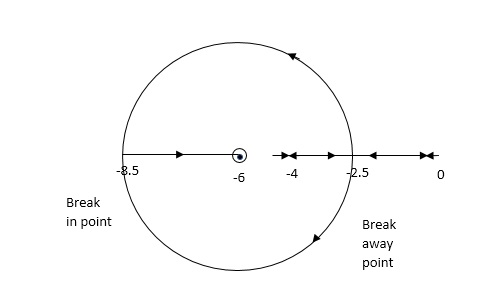
G(S) = K(S + 6)/S(S + 4)
Number of poles = 2(S = 0, -4)
1 + G(S)H(S) = 0 1 + K(S + 6)/S(S + 4) = 0 dk/ds = 0 S2 + 12S + 24 = 0 S = -9.5, -2.5 Breakaway point is at -2.5 and Break in point is at -9.5.
G( + jw) = K( + jw + 6)/( + jw)( + jw + 4 ) = +- π tan-1 w/ + 6 - tan-1 w/ – tan-1 w / + 4 = - π taking tan of both sides. w/ + w/ + 4 / 1 – w/ w/ + 4 = tan π + w / + 6 / 1 - tan π w/ + 6 w/ + w/ + 4 = w/ + 6[ 1 – w2 / ( + 4) ] (2 + 4)( + 6) = (2 + 4 – w2) 2 2 + 12 + 4 + 24 = 2 + 4 – w2 22 + 12 + 24 = 2 – w2 2 + 12 – w2 + 24 = 0 Adding 36 on both sides ( + 6)2 + (w + 0)2 = 12 The above equation shows circle with radius 3.46 and center(-6, 0) the plot is shown in figure.6. |
|
Fig-6 Root Locus for G(S) = K(S + 6)/S(S + 4)
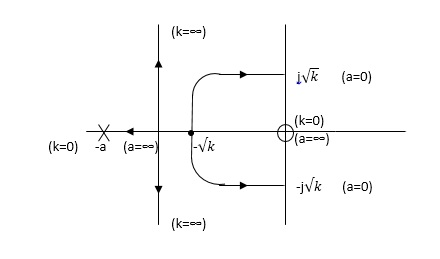
Considering the following characteristic equation.
S2 + as + K = 0
The root contours can be plotted by varying both the parameters ‘a’ and ‘k’. the basic steps involved are mentioned below.
- Sketch the root locus when ‘k’ is varied from 0 to ∞ assuming ‘a’ as constant.
- Sketch the root locus when ‘a’ is varied from 0 to ∞ assuming ‘k’ as constant.
- Sketch the root locus when ‘k’ and ‘a’ both are varied from 0 to ∞.
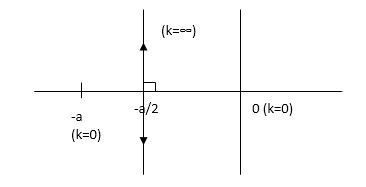
For characteristic equation, S2 + aS + k = 0. Keeping ‘a’ constant 1 + G(S)H(S) = 0 S2 + as[1 + K/S2 + as] = 0 1 + K/S2 + as = 0 The open loop transfer function will be G(S) = K/S(S + a)
Asymptote = (2q + 1)180/P – 2 q = 0, …..(p – 2 - 1) For q = 0 Asymptote = 900 For q = 1 Asymptote = 2700
Centroid = -a/2 The plot will be |
|
Fig 7 Centroid Location on plot
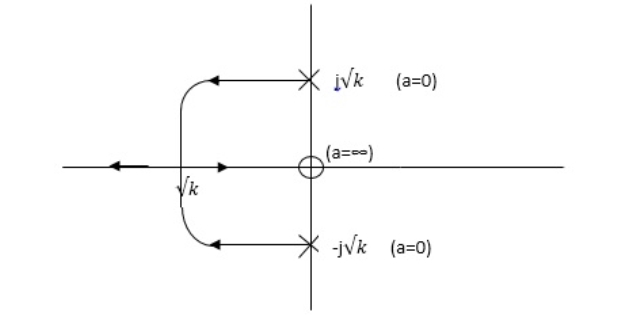
Varying ‘a’ keeping ‘k’ constant. Finding open loop transfer function.
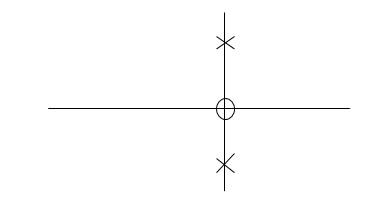
S2 + aS + K = 0 (S2 + K)[ 1 + aS/S2 + k ] = 0 1 + aS/S2 + K = 0 G(S)H(S) = aS/S2 + K
Number of poles = 2(S = +-j√K)
Asymptote = (2q + 1)180/P – Z q = 0, - - (p-z-1) For q = 0, Asymptote = 1800.
Centroid = ∑ Real part of poles - ∑ Real part of zero / P – Z Centroid = 0.
φD = (2q + 1)1800 + φ. ø = ∠Z –∠P. |
|
Fig 8 Location of Poles and Zeros |
φ = LZ – LP = 90 – 90 φ = 0 For q = 0 φD = (2q + 1)1800 + φ. φD = 1800
S2 + aS + K = 0 S2 + K/S = -a -da/ds = ϱ(2S) – (S2 + K) / S2 2S2 – S2 – K – w S = +-√K. |
|
Fig 9 Root Contour varying a keeping k constant
When varying both ‘a’ and ‘K’
|
Fig 10 Root Contour varying both a and k
0 < K < ∞
0 < a < ∞
Absolutely stable: If the root locus (all the branches) lies within the left side of S-plane it is absolutely stable.
Conditionally Stable: If some part of the root locus lies on the left half and same
Part on the right of S-plane then it is conditionally stable.
Unstable: If the root locus lies completely on right side of S-plane then it is unstable.
The values of S which satisfy both the angle and magnitude conditions are the roots of the characteristic equation.
Angle condition: -
LG(S)H(S) = +-1800(2 KH) (K = 1,2,3,--)
If angle is odd multiple of 1800 it satisfies above condition.
Magnitude condition:
| G(S)H(S) = 1 | at any point on root locus. The magnitude condition can be applied only if angle condition is satisfied.
Key takeaway
If the root locus lies completely on right side of S-plane then it is unstable.
If some part of the root locus lies on the left half and same part on the right of S-plane then it is conditionally stable.
If the root locus (all the branches) lies within the left side of S-plane it is absolutely stable.
Effect of Addition of Poles:
1) The root locus is shifted towards imaginary axis.
2) The system becomes oscillatory.
3) The stability of system decreases.
4) The settling time increases.
5) The range of k reduces.
Effect of addition of zeros
1) The root locus shifts away from imaginary axis.
2) Stability of system increases.
3) The settling time decreases.
4) The gain margin increases.
5) The system becomes less oscillatory.
References:
1. “Control System Engineering”, Norman S. Nise,John willey and Sons, 6th Edition, 2015.
2. “Control System Engineering”,I.J. Nagrath and M. Gopal,New age International publication, 5th Edition, 2014.
3. “Modern Control Engineering”, Katsuhiko Ogata,Prentice Hall of India Pvt
Ltd, 5th edition.
4. “Automatic Control System”, Benjamin C. Kuo, Prentice Hall of India Pvt Ltd, Wiley publication, 9th edition