1.1 Introduction to DSP system | unit 1 dft and fft

DSP

UNIT - 1

DFT and FFT

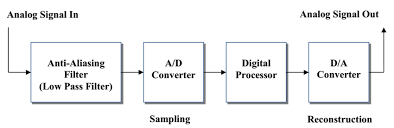
Fig.1: Block diagram of DSP system

To perform the processing digitally, there is a need for an interface between the analog signal and the digital processor. This interface is called an analog-to-digital (A/D) converter. The output of the A to D converter is a digital signal that is appropriate as an input to the digital processor.

The digital signal processor may be a large programmable digital computer or a small microprocessor programmed to perform the desired operations on the input signal. It may also be a hardwired digital processor configured to perform a specified set of operations on the input signal.

Programmable machines provide the flexibility to change the signal processing operations through a change in the software, whereas hardwired machines are difficult to reconfigure. Consequently, programmable signal processors are in very common use.

On the other hand, when signal processing operations are well defined, a hardwired implementation of the operations can be optimized, resulting in a cheaper signal processor and, usually, one that runs faster than its programmable counterpart.

In applications where the digital output from the digital signal processor is to be given to the user in analog form, such as in speech communications, we must provide another interface from the digital domain to analog domain. Such an interface is called a digital-to-analog (D/A) converter. Thus the signal is provided to the user in analog form.

However, there are other practical applications involving signal analysis, where the desired information is conveyed in digital form and no D/A converter is required. For example, in the digital processing of radar signals, the information extracted from the radar signal, such as the position of the aircraft and its speed, may simply be printed on paper. There is no need for a D/A converter in this case.

1.2 DFT, Relation between DFT and Z Transform

The discrete Fourier transform transforms a sequence of N complex numbers 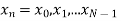into another sequence of complex numbers

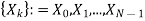which is defined by

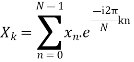
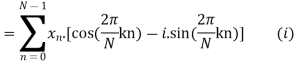
Example:

Let N =4 and

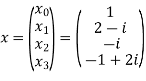
Here we demonstrate how to calculate the DFT of x using equation (1)

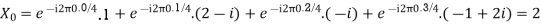
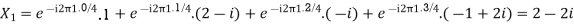
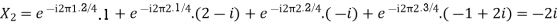
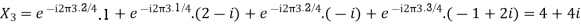
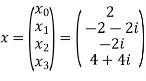
Relation between DFT and Z Transform

1.3 Properties of DFT

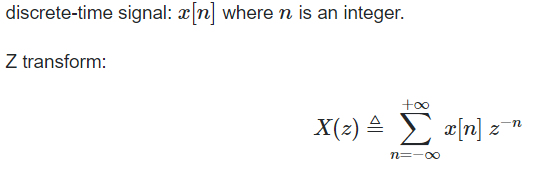
Linear Property

If x(t) -> X(w)

Y(t) -> Y(w) then

a x(t) + b y(t) -> a X(w) +b Y(w)

Time Shifting Property

If x(t)⟷F.TX(ω)

Then Time shifting property states that

x(t−t0)⟷F.T e−jω0t X(ω)

Frequency Shifting Property

If x(t)⟷X(ω)

Then frequency shifting property states that

ejω0t.x(t)⟷X(ω−ω0)

Time Reversal Property

If x(t)⟷X(ω)

Then Time reversal property states that

x(−t)⟷X(−ω)

Differentiation Property

If x(t)⟷X(ω)

Then Differentiation property states that

dx(t)dt ⟷jω.X(ω)

dnx(t)dtn⟷(jω)n.X(ω)

Integration Property

Integration property states that

∫x(t)dt⟷1jω X(ω)

Then

∭...∫x(t)dt⟷(jω)n X(ω)

Multiplication and Convolution Properties

If x(t)⟷X(ω)

y(t)⟷Y(ω)

Then multiplication property states that

x(t).y(t)⟷X(ω)∗Y(ω)

and convolution property states that

x(t)∗y(t)⟷1/2πX(ω).Y(ω)

Numerical:

Compute the N-point DFT of x(n)=3δ(n).

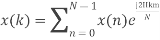
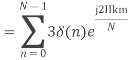
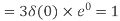
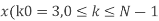
2. Compute the N-point DFT of x(n)=7(n−n0)

Solution − We know that,

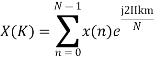
Substituting the value of x(n),

1.4 Circular convolution

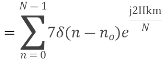
Let us take two finite duration sequences ,having integer length as N. Their DI are 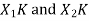reapectively which is shown below

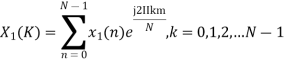
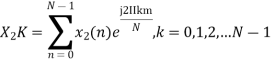
Now we will try to find the DFT of another sequence 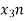, which is given by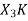

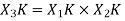
By taking the IDFT of the above we get

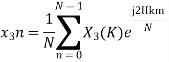
After solving the above equation finally we get

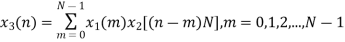
Methods of Circular Convolution

Generally, there are two methods, which are adopted to perform circular convolution and they are −

Concentric circle method,

Matrix multiplication method.

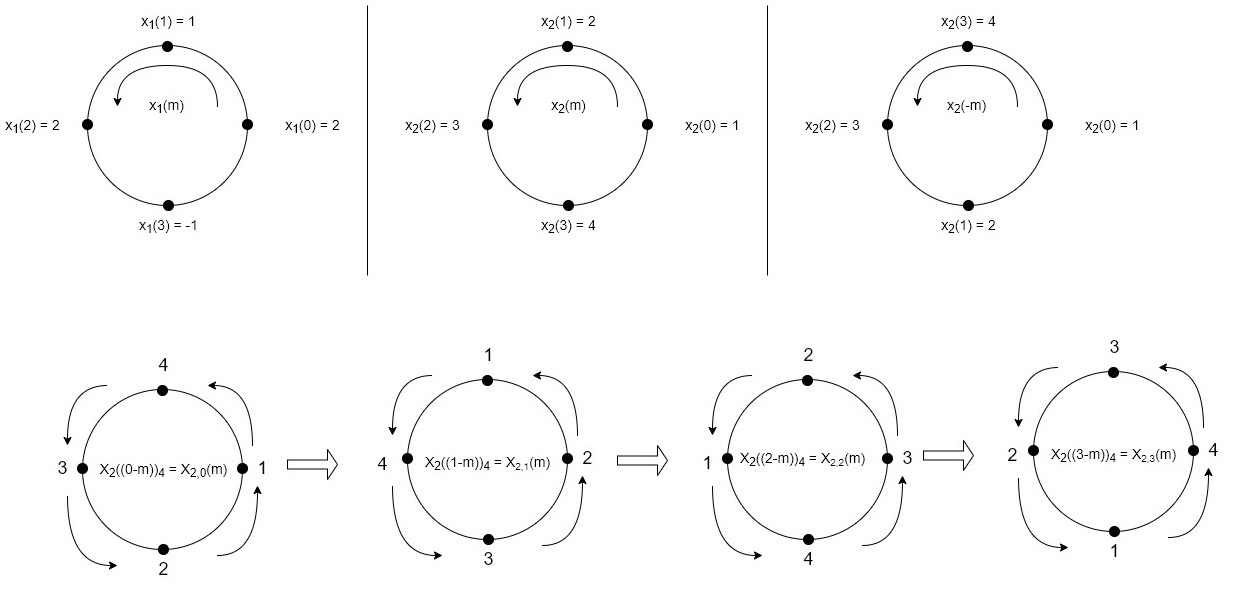
Concentric Circle Method

Let x1(n) and x2(n) be two given sequences. The steps followed for circular convolution of x1(n) and x2(n) are

Take two concentric circles. Plot N samples of x1(n) on the circumference of the outer circle maintaining equal distance successive points maintaining equal distance successive points in anti-clockwise direction.

For plotting x2(n), plot N samples of x2(n) in clockwise direction on the inner circle, starting sample placed at the same point as 0th sample of x1(n)

Multiply corresponding samples on the two circles and add them to get output.

Rotate the inner circle anti-clockwise with one sample at a time.

Matrix Multiplication Method

Matrix method represents the two-given sequence x1(n) and x2(n) in matrix form.

One of the given sequences is repeated via circular shift of one sample at a time to form a N X N matrix.

The other sequence is represented as column matrix.

The multiplication of two matrices give the result of circular convolution.

Numerical:

Perform circular convolution of the two sequences, x1(n)= {2,1,2,-1} and x2(n)= {1,2,3,4}

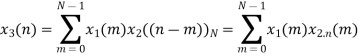
(2)

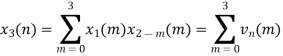
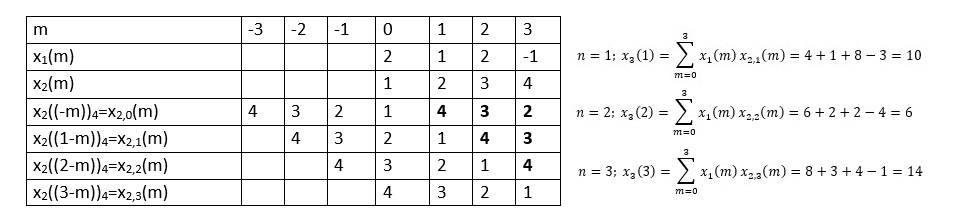
When n=0;

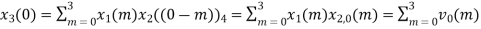
The sum of samples of v0(m) gives x3(0)

⸫ x3(0)=2+4+6-2=10

When n=1;

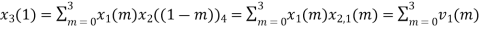
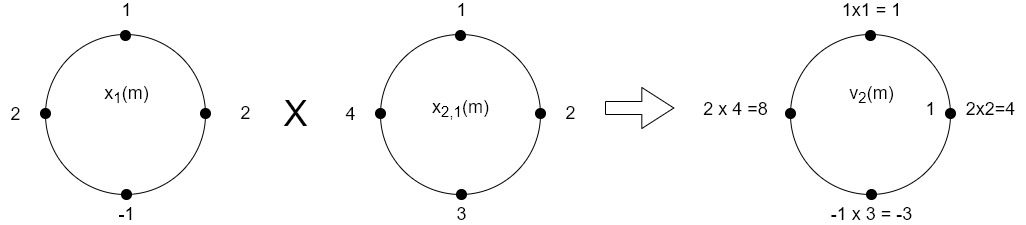
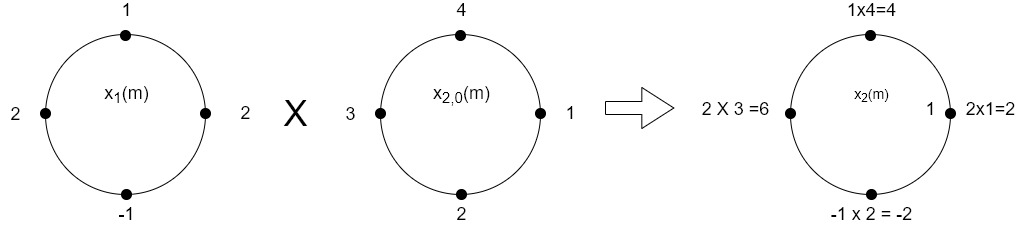
The sum of samples of v1(m) gives x2(1)

⸫ x3(1)=4 + 1 +8-3=10

(3)When n=2;

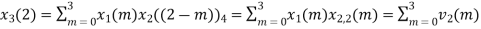
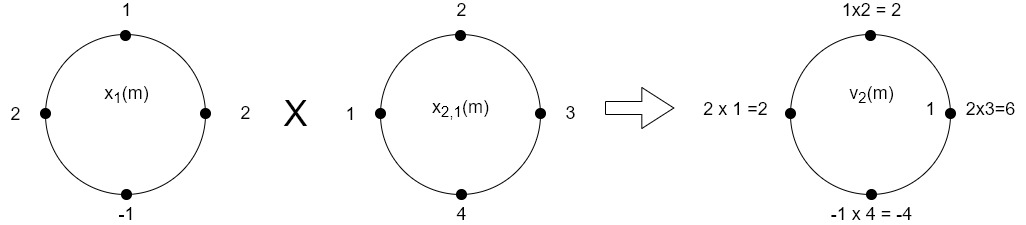
The sum of samples of v2(m) gives x3(2)

⸫ x3(2)=6+2+2-4=6

(4) When n=3;

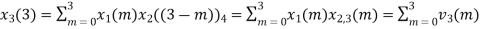
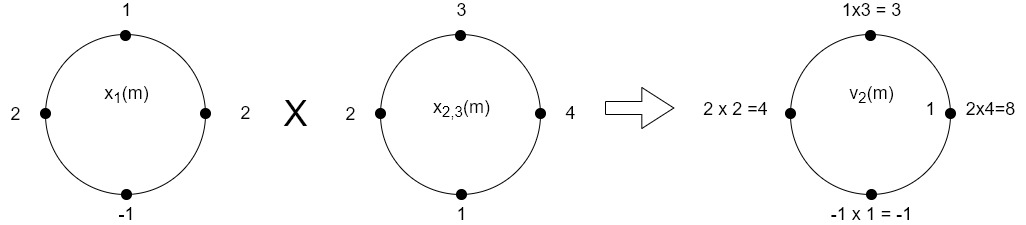
The sum of samples of v3(m) gives x3(3)

⸫ x3(3)=8+ 3+ 4-1= 14

x3(n)={10,10,6,14}

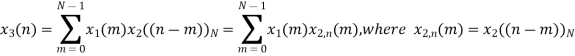
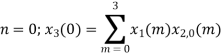
= x1(0) x x2,0(0) + x1(1) x2,0(1) + x1(2) x2,0(2) + x1(3) x2,0(3)

= 2 x 1 + 1 x 4 + 2 x 3 + (-1) x 2 = 2 +4 +6 -2 =10

1.5 IDFT

The inverse DFT (IDFT) transforms N discrete-frequency samples to the same number of discrete-time samples. The IDFT has a form very similar to the DFT and can thus also be computed efficiently using FFTs.

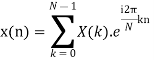
1.6 DIT FFT & DIF FFT algorithm implementation

Decimation-in-time algorithm

This algorithm is known as Radix-2 DIT-FFT algorithm which means the number of output points N can be expressed as a power of 2 that is N = 2M where M is an integer.

Let x(n) be a sequence where N is assumed to be a power of 2. Decimate or break this sequence into two sequences of length N/2 where one sequence consists of even-indexed values of x(n) and the other of odd-indexed values of x(n).

xe(n) = x(2n) n= 0,1,……….. N/2-1

xo(n) = x(2n+1) n= 0,1,……….. N/2 -1

The N-pt DFT of x(n) can be written as

X(k) = WN nk where k=0,1……….. N-1.

Separating x(n) into even and odd indexed values of x(n) we obtain

X(k) = 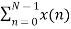W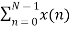N nk + WN nk

( n even) (n odd)

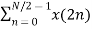= WN 2nk + 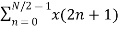WN (2n+1)k

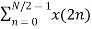= WN 2nk + Wnk 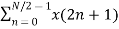W N 2nk

X(k) = 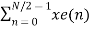WN 2nk + Wnk 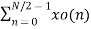W N 2nk

WN2 =( e-j2π/N) 2 = e-j2π/N/2 = W N/2 .

WN2 = W N/2

X(k) = 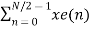W N/2n k + WNk 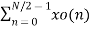WN/2kn

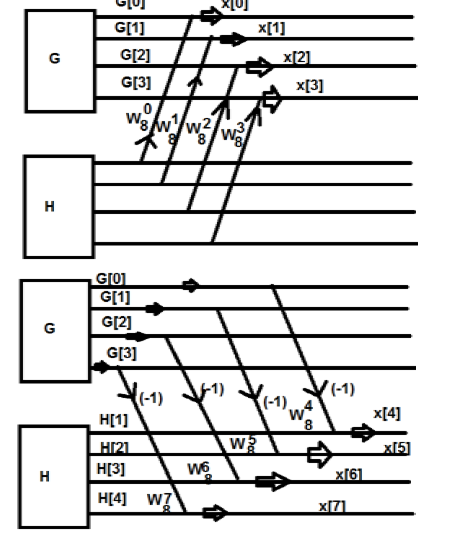
W84 = -1

W8 5 = - W 81

W86 = - W82

W87 = - W83

G(0) – H(0) = x(4)

G(1) - W 81 H(1) = x(5)

G(2) - W82 H(2) = x(6)

G(3) - W83 H(3) = x(7)

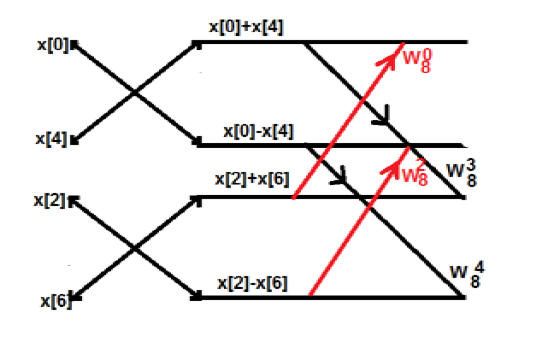
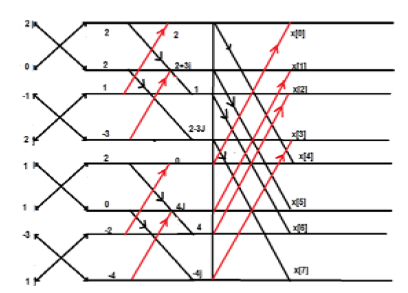
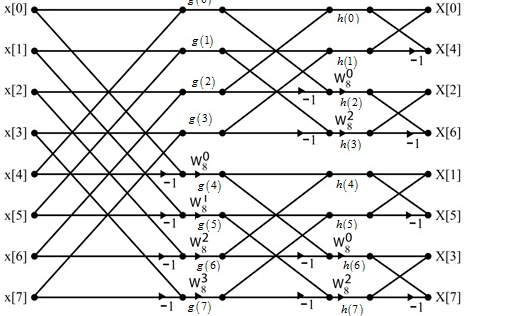
Consider the sequence x[n]={ 2,1,-1,-3,0,1,2,1}. Calculate the FFT.

Arrange the sequence as x(0) x(4) x(2) x(6) x(1) x(5) x(3) x(7)

Since N=8 find the values W8 0 to W 87

Apply the butterfly diagram to obtain the values.

DIF-FFT ALGORITHM

Decimation in Frequency FFT

Apart from time sequence, an N-point sequence can also be represented in frequency. Let us take a four-point sequence to understand it better.

Let the sequence be x[0],x[1],x[2],x[3]………..x[7]

Mathematically, this sequence can be written as;

X(k) = 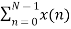WN n-k where k=0,1……….. N-1.

Now let us make one group of sequence number 0 to 3 and another group of sequence 4 to 7. Now, mathematically this can be shown as

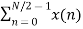= W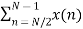N nk + WN nk

Let us replace n by r, where r = 0, 1 , 2….N/2−1.

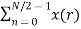= W N/2 nr

We take the first four points x[0],x[1],x[2],x[3] initially, and try to represent them mathematically as follows –

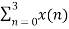W 8 nk + 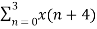W8 (n+4) k

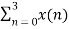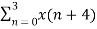= + W8 (n+4) k

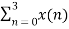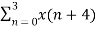= + { W8 (4) k } W8 nk

X[0] = 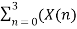+ X[n+4]

X[1] = 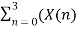+ X[n+4]) W8 nk

= X(0) – X(4) + (x[1] – X[5]) W8 1 + ( X[2] – X[6] )W82 + X(3) – X(7) W8 3

Find the DIF –FFT of the sequence x(n)= { 1,-1,-1,1,1,1,-1} using Dif-FFT algorithm.

X(0)= 20 X(4) =0

X(1) = -5.828- j2.414 X(5) = -0.1716 + j 0.4141

X(2) = 0 X(6) = 0

X(3) = -0.171 – j 0.4142 X(7) = -5.8284 + j2.4142

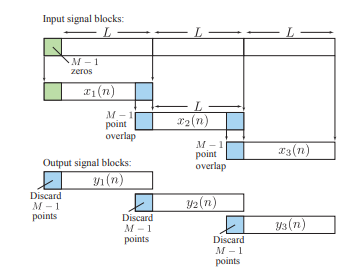
1.7 Fast convolution signal: Overlap save & overlap-add algorithm segmentation

Overlap add method

Break the input signal x(n) into non overlapping blocks

of length L.

Zero pad h(n) to be of length N=L+M-1.

Take N-DFT of h(n) to give H(k), k = 0,1,…,N-1.

Fop each block m

Zero pad
to be length of N-L+M-1.
Take N-DFT of
to give
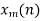, k=0,1,…,N-1.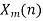
Multiply
=
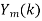. H(k), k=0,1,…,N-1.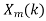
Take N-DFT of
to give
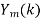, n=0,1,…,N-1.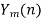

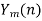
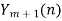
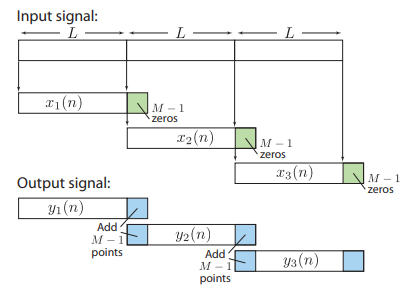
Form y(n) by overlapping the last M-1 samples of

with the first M-1 samples of

and adding the result.

Overlap save method

Insert M-1 zeros at the beginning of the input sequence x (n).

Break the padded input signal into overlapping blocks

of length N = L +M-1 where the overlap length is M-1.

Zero pad h (n) to be of length N = L+M-1.

Take N-DFT of h (n) to give H (k), k= 0,1,…,N-1.

For each block m\

Take N-DFT of
to give
, k= 0,1,…,N-1.
Multiply
=
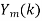. H (k), k=0,1,…,N-1.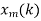
Take N-DFT of
to give
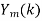, n=0,1,…,N-1.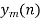
Discard the first M-1 points of each output block
.

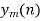
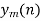
Form y (n) by appending the remaining i.e. last L samples of each block

1.8 Circular correlation

Let X be a linear random variable, and Θ be a circular random variable. We observe data (x1,θ1),…,(xn,θn) on (X,Θ). In our case, n denotes cells, xi denotes log2 expression (CPM) of a selected gene, and θi denotes the angle of cell i on the unit circle formed by GFP and RFP.

Θ measures directions in 2-dimensions and can be represented as unit vectors u in the plane, i.e., as points on the sphere Sp−1={u:uT u=1}, the (p-1) dimensional sphere with unit radius and centre at the origin, where p=2. u is thus defined by

u= (cosΘ, sinΘ)T

This definition of Θ is also known as the embedding approach, where the sphere Sp−1 is regarded as a subset of Rp.

Circular-circular correlation picks up more interesting patterns than circular-linear correlation. In circular-linear correlation, the linear variable is implied to follow a sinusoidal pattern. This assumption is quite limited, and may explain why many of the genes detected significant in circ-linear case are not significant in cir-cir case.

Although circular-circular correlation detects interesting patterns, the definition of this particular definition of circular-circular correlation (there are other ones) results in a measure that is phase-sensitive. For example, when the phase shift is pi/2, the two variables have a correlation of zero.

1.9 IFFT

IFFT is a fast algorithm to perform inverse (or backward) Fourier transform (IDFT), which undoes the process of DFT. IDFT of a sequence {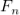 F_n } that can be defined as:

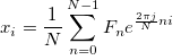
$x_i=\frac{1}{N}\sum _{n=0}^{N-1}F_ne^{\frac{2\pi j}{N}ni}$

1.10 DFT properties of circular correlation

The circular cross-correlation of two sequences in the time domain is equivalent to the multiplication of DFT of one sequence with the complex conjugate DFT of the other sequence.

Mathematical representation:

For x(n) and y(n), circular correlation rxy(l) is

rxy(l) 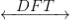$\underleftrightarrow { \quad DFT\quad }$ Rxy(k) = X(k).Y*(k)