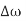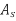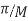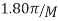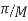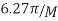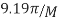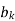Design an FIR lowpass filter using
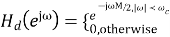
Inverse Fourier transforming we find that
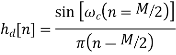
Assuming 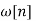 is symmetric about M/2, then the linear phaseh[n] is
is symmetric about M/2, then the linear phaseh[n] is
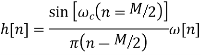
The relevant lowpass amplitude specifications of interest are shown below
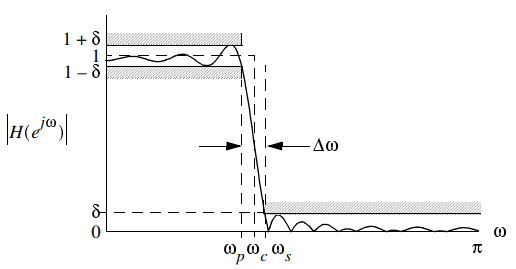
Note that the stopband attenuation in Db is 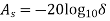 and the peak ripple in Db is
and the peak ripple in Db is 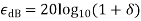
For the Rectangular, Bartlett, Hanning, Hamming and Blackman window functions the relevant design data is given in the following table
Window Characteristic for FIR Filter Design
Window Type | Transition Bandwidth | Minimum Stopband Attenuation, | Equivalent Kaiser Window |
Rectangular | 1.81 | 21dB | 0 |
Bartlett |
| 25dB | 1.33 |
Hanning | 5.01 | 44dB | 3.86 |
Hamming |
| 53dB | 4.86 |
Blackman |
| 74dB | 7.04 |
The frequency sampling method is use to design recursive and non-recursive FIR filters for both standard frequency selective filters and with arbitrary frequency response. The main idea of the frequency sampling design method is that a desired frequency response can be approximated by sampling it at N evenly spaced points and then obtaining N-point filter response.
A continuous frequency response is then calculated as an interpolation of the sampled frequency response. The approximation error would then be exactly zero at the sampling frequencies and would be finite in frequencies between them. The smoother the frequency response being approximated, the smaller will be the error of interpolation between the sample points.
There are two distinct types of Non-Recursive Frequency Sampling method of FIR filter design, depending on where the initial frequency sample occurred. The type 1 designs have the initial point at ω=0, whereas the type 2 designs have the initial point at f=1/2N or ω=π/N.
Procedure for Type I design
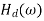
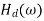
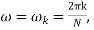
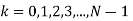
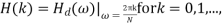
Desired filter coefficients
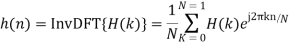
for linear phase filter with positive symmetrical impulse response,
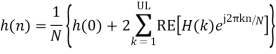
4) take z transform of the impulse response h (n) to get the filter transfer function H (z)
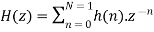
Procedure for Type 2 Design
(Same steps as above expect step 2)
2) Samples  at N points by taking
at N points by taking 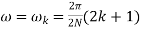 where
where 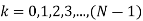 generate the sequence H (z)
generate the sequence H (z)
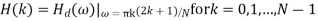
Type 2 frequency samples gives additional flexibility in the design method to satisfy the desired frequency response at a second possible set of frequencies.
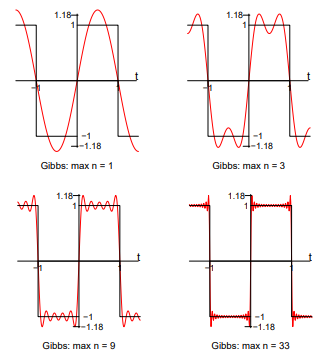
In practice it may be impossible to use all the terms of a Fourier series. For example, suppose we have a device that manipulates a periodic signal by first finding the Fourier series of the signal, then manipulating the sinusoidal components, and, finally, reconstructing the signal by adding up the modified Fourier series. Such a device will only be able to use a finite number of terms of the series.
Gibbs’ phenomenon occurs near a jump discontinuity in the signal. It says that no matter how many terms you include in your Fourier series there will always be an error in the form of an overshoot near the discontinuity.
The overshoot always be about 9% of the size of the jump. We illustrate with the example. of the square wave sq(t). The Fourier series of sq(t) fits it well at points of continuity. But there is always an overshoot of about .18 (9% of the jump of 2) near the points of discontinuity.
In these figures, for example, ’max n=9’ means we we included the terms for n = 1, 3, 5, 7 and 9 in the Fourier sum
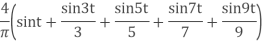
Windowing method
Let the frequency response of the desired LTI ststem we wish to approximate be given by
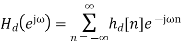
Where 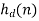 is the corresponding impulse response.
is the corresponding impulse response.
Consider obtaining a casual FIR filter that approximates 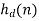 by letting
by letting
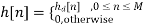
the FIR filter then has frequency response
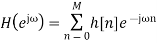
Note that sibce we can write
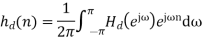
We are actually forming a finite Fourier series approximation to 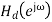
Since the ideal 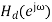 may contain discontinuities at the band edges, truncation of the Fourier series will result in the Gibbs phenomenon.
may contain discontinuities at the band edges, truncation of the Fourier series will result in the Gibbs phenomenon.
To allow for a less abrupt Fourier series truncation and hence reduce Gibbs phenomenon oscillations, we may generalize h [n] by writing
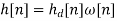
where 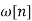 is a finite duration window function of length M +1.
is a finite duration window function of length M +1.
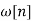
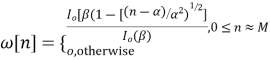
Where 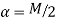
2. Choose 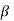 for the specified
for the specified 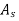 .
.
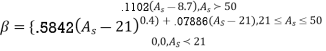
3. The window length M is then chosen to satisfy
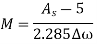
4. The value for 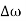 is chosen as before
is chosen as before
Note: Using the Kaiser empirical formula M can be determined over a wide range of 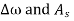 values to within
values to within 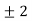 . Very little if any literation is needed.
. Very little if any literation is needed.
Design an FIR lowpass using the windowing method such that 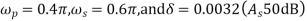
From the window characteristic we immediately see that for 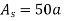 Hammering window will work.
Hammering window will work.
To find M set
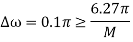
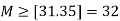
The cut off frequency is
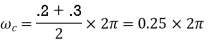
If a Kaiser window is desired, then for  choose
choose
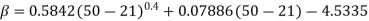
The prescribed value for M should be
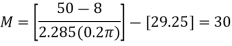
Numerical:
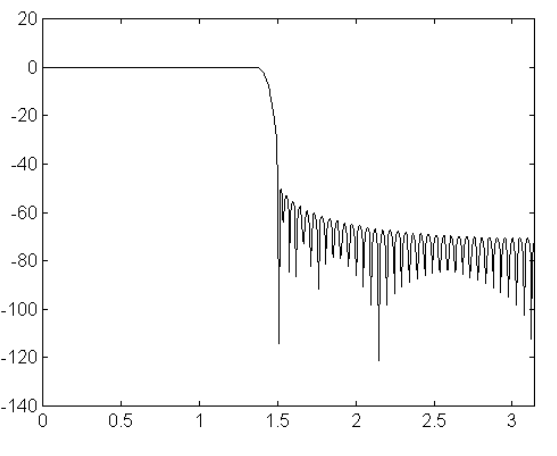
We want to design a Low Pass FIR Filter with the following characteristics: Solutions_Chapter4[1].nb 5Passband 10kHz, Stopband 11kHz, with attenuation of 50dB, Sampling frequency 44kHz Determine the causal impulse response hn, and an expression for the phase within the passband.
Solution:

The direct form is obtained from
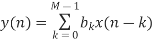
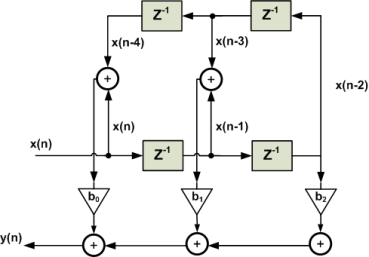
Based on the above equation, we need the current input sample and M−1 previous samples of the input to produce an output point. For M=5, we can simply obtain the following diagram from Equation 1.
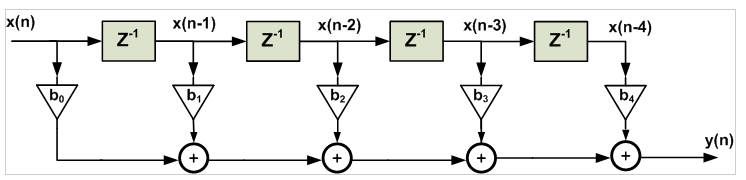
On the other hand, for a linear-phase FIR filter, we observe the following symmetry in coefficients of the difference equation
he structure obtained from the above equation is shown in Figure 2. While Figure 1 requires five multipliers, employing the symmetry of a linear-phase FIR filter, we can implement the filter using only three multipliers. This example shows that for an odd M, the symmetry property reduces the number of multipliers of an (M−1)th-order FIR filter from M to M+1/2.
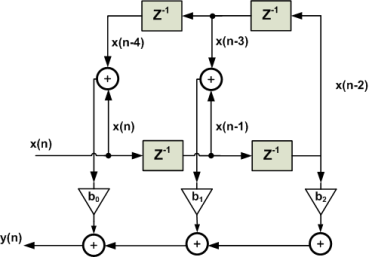
The cascade structure is obtained from the system function H(z). The idea is to decompose the target system function into a cascade of second-order FIR systems. In other words, we need to find second-order systems which satisfy
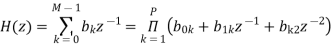
where P is the integer part of M/2. For example, M=5, H(z) will be a polynomial of degree four which can be decomposed into two second-order sections. Each of these second-order filters can be realized using a direct form structure. It is desirable to set a pair of complex-conjugate roots for each of the second-order sections so that the coefficients become real.
Assume that we need to implement the nine-tap FIR filter given by the following table using a cascade structure.
k | 4 | 3 and 5 | 2 and 6 | 1 and 7 | 0 and 8 |
| 0.3333 | 0.2813 | 0.1497 | 0 | -0.0977 |
Solution:
The system function of this filter is
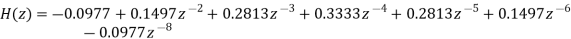
It can be show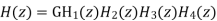
Where
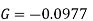
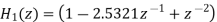
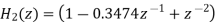
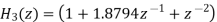
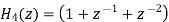
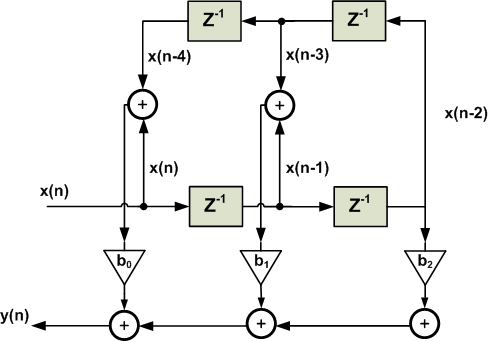

The parallel form is obtained from
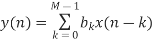
Based on the above equation, we need the current input sample and M−1 previous samples of the input to produce an output point. For M=5, we can simply obtain the following diagram from Equation 1.
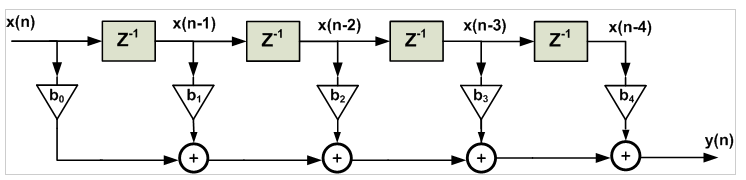
On the other hand, for a linear-phase FIR filter, we observe the following symmetry in coefficients of the difference equation
he structure obtained from the above equation is shown in Figure 2. While Figure 1 requires five multipliers, employing the symmetry of a linear-phase FIR filter, we can implement the filter using only three multipliers. This example shows that for an odd M, the symmetry property reduces the number of multipliers of an (M−1)th-order FIR filter from M to M+1/2.
1. John G Prokis , “Digital Signal Processing ,Principles, Algorithms and
Application”,PHI
2. S.K.Mitra, “Digital Signal Processing”, TMH
3. E. C. Ifleachor and B. W. Jervis, “Digital Signal Processing- A Practical
Approach”, Second Edition, Pearson education.
4.Avtar Singh, S. Srinivasan, “Digital Signal Processing Implementation using DSP,
Microprocessors with examples from TMS 320C6XXX”, Thomas Publication.