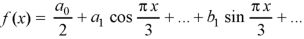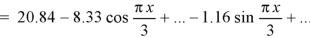UNIT 3

Fourier series

3.1. Fourier series- Even and odd functions

Periodic functions-

If the value of the function ( y-axis) repeats itself on x-axis, then the function is called periodic function.

Suppose f(x) is a function, then

If          f(x) = f(x + t) = f (x + 2t) =    …………….

Then t is called the periodic of the function f(x).

Suppose of we take sin x, then it repeats its value after the period of 2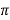such that, we write this as

Sin x = sin (x + 2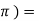 sin ( x + 4) ………….

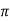We can say that sin x is a periodic function with the period of 2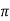

First we will define the Fourier series-

A series of the form,

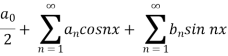
Is called fourier series , where

are constants.

Any periodic function can be expanded in the form of fourier series.

Determination of 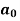 ,  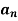 , 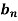of Fourier series-

We know that, the fourier series,

f(x) = 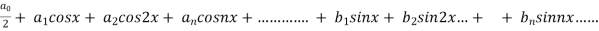  ------------ eq.(1)

To find –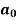

Integrate equation (1) on both sides, from 0 to 2π

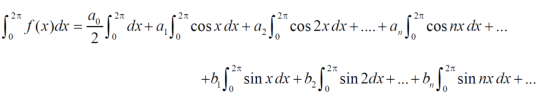
Which gives,

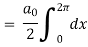
To find -

Multiply each side of eq. (1) by cosnx  and integrate from 0 to 2π

We get,

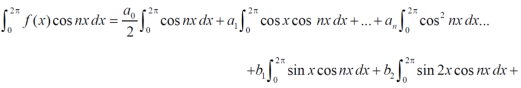
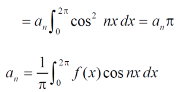
Similarly we can find 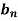by , multiplying eq. (1) by sin nx and integrating from 0 to  2π

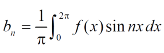
Example: Find the fourier series of the function f(x) = x      where 0 < x < 2 π

Sol. We know that, from fourier series,

f(x) =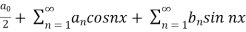

First we will find ,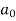

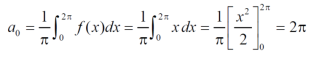
Now,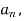

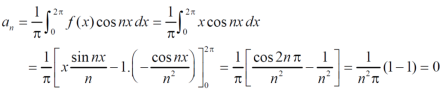
And ,

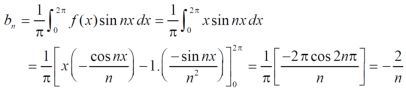
Put these value in fourier series, we get

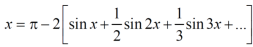
Example: Find the fourier series for f(x) = x / 2 over the interval 0 < x < 2π

And has period 2π

Sol. First we will find

  = 

=

=

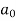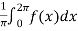
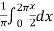
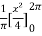
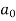= π

   =   π

Similarly,

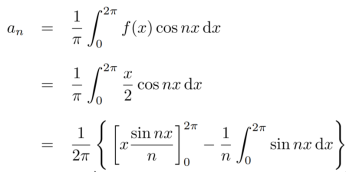
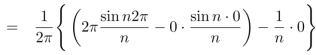
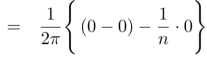
Which gives,     =   0

Now,

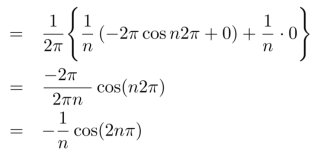
We get,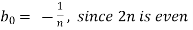

We know that, the fourier series

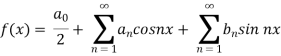
Put these values in fourier series, we get

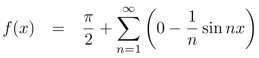
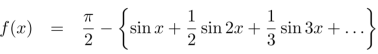
Dirichlet’s conditions for representation by a Fourier series-

Let f(x) be a function defined in C < x < C + 2L such that

1)     f(x) is defined and single valued in the given internal also. 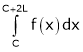exist.

2)     f(x) may have finite number of finite discontinuities in the interval.

3)     f(x) may have finite number of maxima or minima in the given interval.

Fourier series of even and odd function

Odd function-

A function f(x), which is written as ,

f( - x ) = - f(x)

Is known as odd function.

The graph of the odd function looks like-

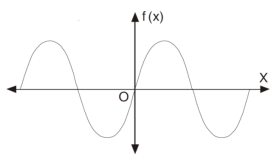
The graph of the function is symmetric about x-axis.

And the area under the curve from -π to π is always zero.(see fig)

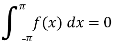
Even function-

If f(-x) = f(x) then the function is known as even function.

The graph of the function f(x) looks like-

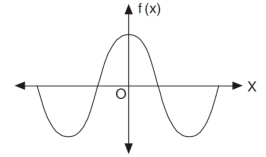
Area under the curve from -π to π  will always be double the area from 0 to π

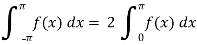
Expansion of an even function-

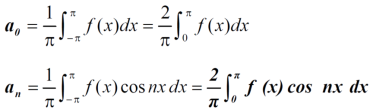
Here cosnx and f(x) are both even functions.

As we know that the product of two even numbers will be even.

Such as product of f(x) and cosnx will always be even.

Now,

Here we see that sin nx is an odd function.

So that we do not need to find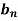

That means the series of an even function contains cosine terms only.

Expansion of an odd function-

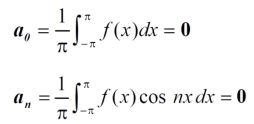
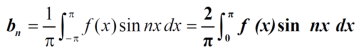
The series of the odd function contains only sine terms.

Example: Find the fourier expression of f(x) = x³ for –π< x <π.

Sol.

Here, we can see that f(x) Is an odd function

So that,

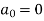and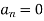

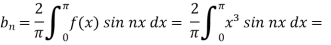
We will use here ,

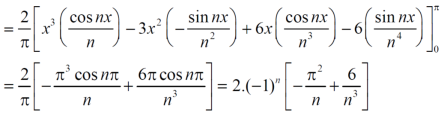
We get the value of f(x),

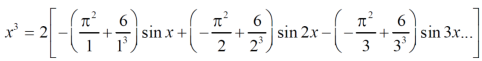
Example: Find the Fourier series expansion of the periodic function of period 2π.

f(x) = x² ,    -π≤x≤π

Sol. The given function is even, so that,

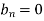
We will find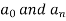

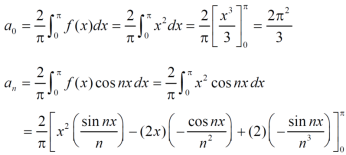
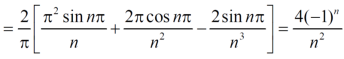
The fourier series will be ,

3.2. Periodic functions- half range sine and cosine series

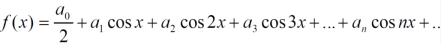
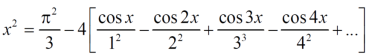
The function is defined in the interval (0,π) and it is immaterial whatever the function may be outside the interval (0,π)

To get the series of cosines only we suppose that f(x) is an even function in the interval (-π,π)

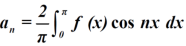
And bn = 0

To expand the as a sine series in the same interval and as an odd function.

Bn = 0.

Example- Find a Fourier series for

; 

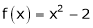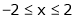
Solution:

Here

; 

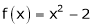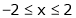
Since f(x) is even function hence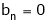

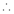It’s Fourier series is

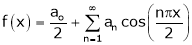     … (1)

Where

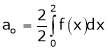
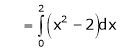
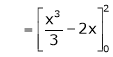
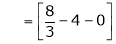
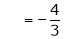
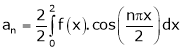
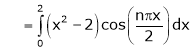
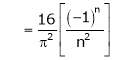
Hence equation (1) becomes,

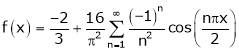
1. Find half range cosine series of in the interval and hence deduce that

a)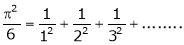    

b)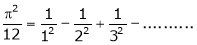   

Solution:

Here

; 

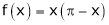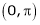
Hence it’s half range cosine series is,

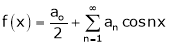       … (1)

Where

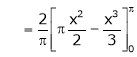
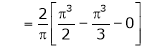
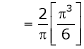
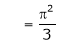
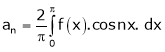
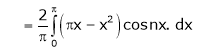
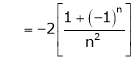
Hence equation (1) becomes,

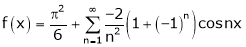
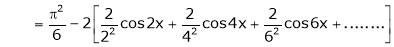
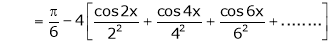    … (2)

Put x = 0, we get

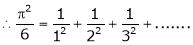
Hence the result

Put 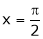 we get,

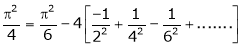
i.e.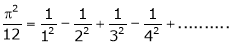

Example: Find the Fourier sine series for the function-

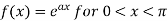
Where ‘a’ is a constant.

Sol. Here we know-

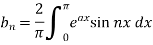
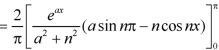
We know that-

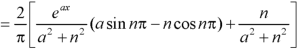
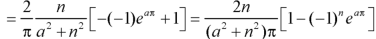
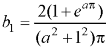
And

3.3. Harmonic analysis

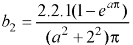
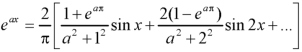
The process of finding the Fourier series for a function given by such values of the function and independent variable is known as harmonic analysis.

We can evaluate the Fourier constant by the formulas given below-

1. To find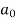

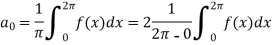
2.To find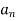

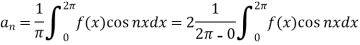
3. To find

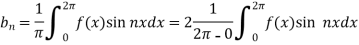
Fundamental of first harmonic- The following term in the Fourier series is called the first harmonic or fundamental harmonic-

Second harmonic-

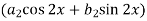
Example: Find the constant terms and the coefficients of the first sine and cosine terms in the Fourier series of f(x) of the following table-

Sol.

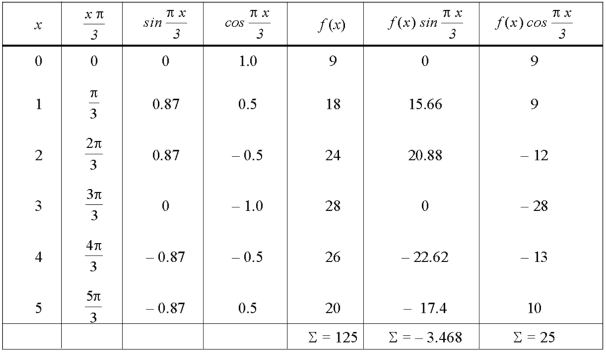
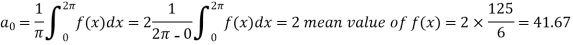
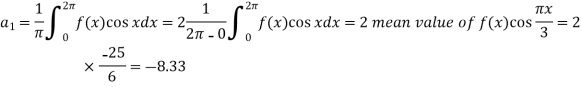
Fourier series is-