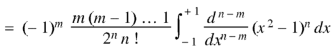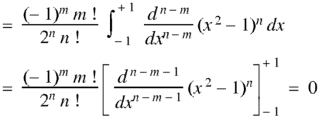UNIT 5
Bessel function
The Bessel equation is-

The solution of this equations will be-
The Bessel function is denoted by 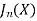 and defined as-
and defined as-

If we put n = 0 then Bessel function becomes-
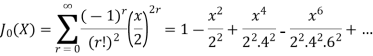
Now if n = 1, then-
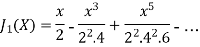
The graph of these two equations will be-
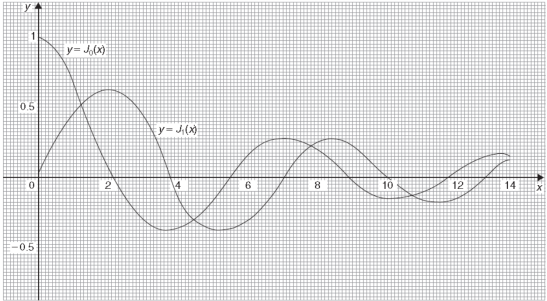
General solution of Bessel equation-

Example: Prove that-
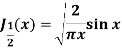
Sol.
As we know that-

Now put n = 1/2 in equation (1), then we get-
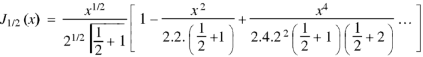
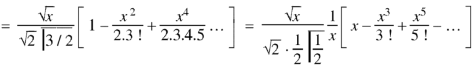
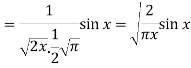
Hence proved.
Example: Prove that-
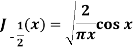
Sol.
Put n = -1/2 in equation (1) of the above question, we get-
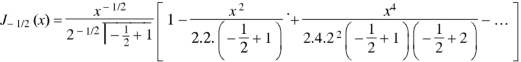
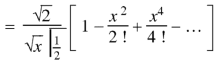
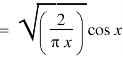
Formula-1: 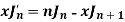
Proof:
As we know that-
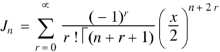
On differentiating with respect to x, we obtain-

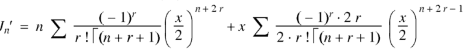
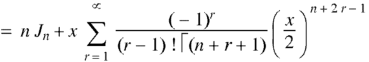
Putting r – 1 = s
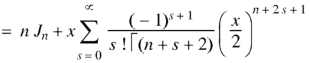
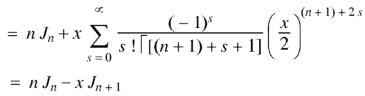
Formula-2: 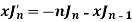
Proof:
We have-

Differentiating w.r.t. x, we get-
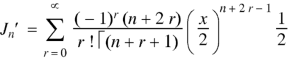
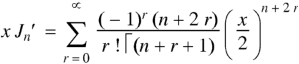
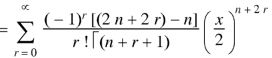

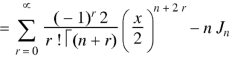
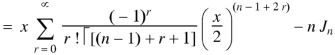
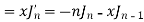
Formula-3: 
Proof: We know that from formula first and second-
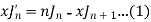
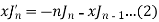
Now adding these two, we get-
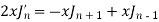
Or
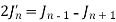
Formula-4: 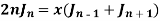
Proof:
We know that-
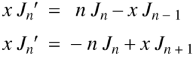
On subtracting, we get-
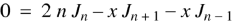
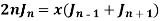
Formula-5: 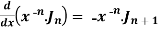
Proof:
We know that-
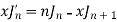
Multiply this by 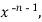 we get-
we get-
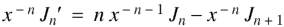
I.e.
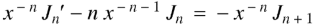
Or
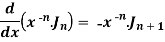
Formula-6: 
Proof:
We know that-
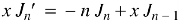
Multiply by  we get-
we get-
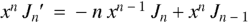
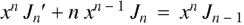
Or
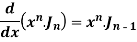
Example: Show that-
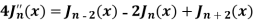
By using recurrence relation.
Sol.
We know that-
The recurrence formula-

On differentiating, we get-
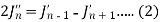
Now replace n by n -1 and n by n+1 in (1), we have-
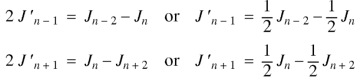
Put the values of 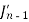 and
and 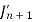 from the above equations in (2), we get-
from the above equations in (2), we get-
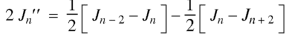

Example: Prove that-
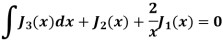
Sol.
We know that- from recurrence formula
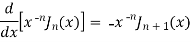
On integrating we get-
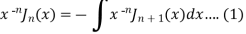
On taking n = 2 in (1), we get-
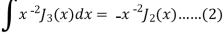
Again-
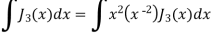
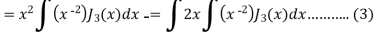
Put the value of 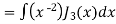 from equation (2) and (3), we get-
from equation (2) and (3), we get-
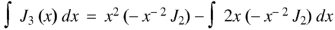
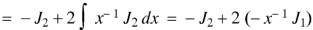
By equation (1), when n = 1
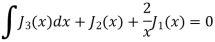
5.3. Generating function for 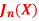
Prove that 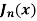 is the coefficient of
is the coefficient of  in the expansion of
in the expansion of 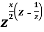
Proof:
As we know that-
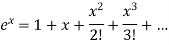
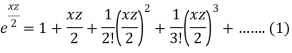
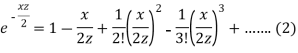
Multiply equation (1) by (2), we get-

Now the coefficient of 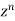 in the product of (3)
in the product of (3)
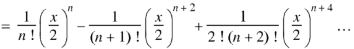
= 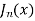
Similarly the coefficient of 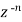 in the product of (3) =
in the product of (3) =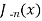
So that-
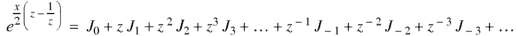
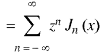
That is why 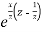 is known as the generating function of Bessel functions
is known as the generating function of Bessel functions
5.4. Legendre polynomials ( – Recurrence formulae &Rodrigue’s formula-
– Recurrence formulae &Rodrigue’s formula-
The Legendre’s equations is-
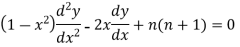
Now the solution of the given equation is the series of descending powers of x is-
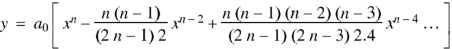
Here 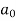 is an arbitrary constant.
is an arbitrary constant.
If n is a positive integer and
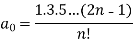
The above solution is 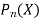
So that-
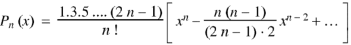
Here 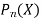 is called the Legendre’s function of first kind.
is called the Legendre’s function of first kind.
Note- Legendre’s equations of second kind is 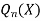 and can be defined as-
and can be defined as-
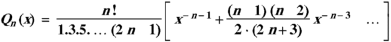
The general solution of Legendre’s equation is-

Here A and B are arbitrary constants.
Rodrigue’s formula-
Rodrigue’s formula can be defined as-
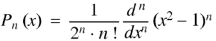
Legendre Polynomials-
We know that by Rodrigue formula-
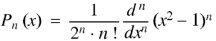
If n = 0, then it becomes-
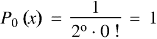
If n = 1,
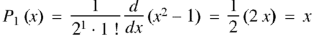
If n = 2,
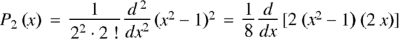
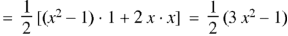
Now putting n =3, 4, 5……..n we get-
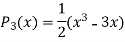
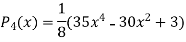
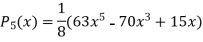
…………………………………..
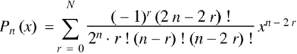
Where N = n/2 if n is even and N = 1/2 (n-1) if n is odd.
Example: Express 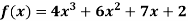 in terms of Legendre polynomials.
in terms of Legendre polynomials.
Sol.
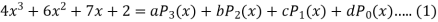
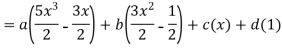
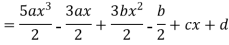
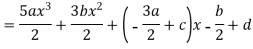
By equating the coefficients of like powers of x, we get-
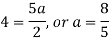
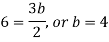
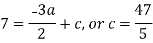
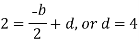
Put these values in equation (1), we get-
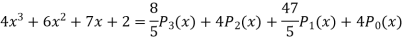
Example: Let 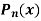 be the Legendre’s polynomial of degree n, then show that for every function f(x) for which the n’th derivative is continuous-
be the Legendre’s polynomial of degree n, then show that for every function f(x) for which the n’th derivative is continuous-
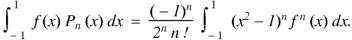
Sol.
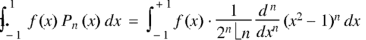
We know that-

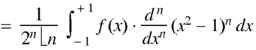
On integrating by parts, we get-
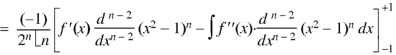
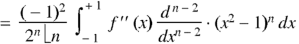
Now integrate (n – 2) times by parts, we get-

Recurrence formulae for 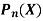 -
-
Formula-1:
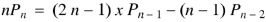
Fromula-2:

Formula-3:
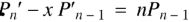
Formula-4:

Formula-5:

Formula-6:
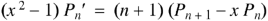
5.5. Generating function for 
Prove that 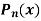 is the coefficient of
is the coefficient of  in the expansion of
in the expansion of 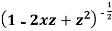 in ascending powers of z.
in ascending powers of z.
Proof:
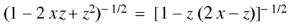
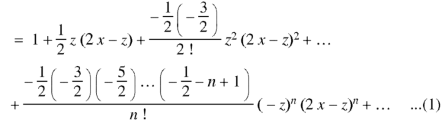
Now coefficient of 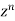 in
in
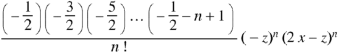
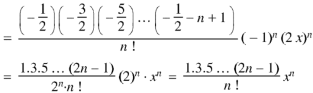
Coefficient of 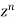 in
in
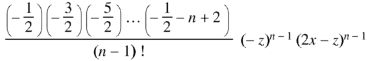
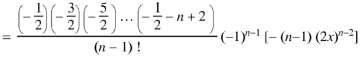
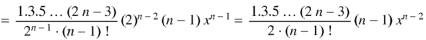
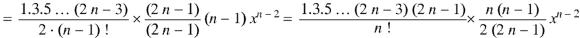
Coefficient of 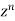 in
in
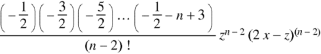
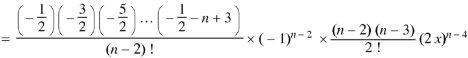

And so on.
Coefficient of 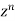 in the expansion of equation (1)-
in the expansion of equation (1)-
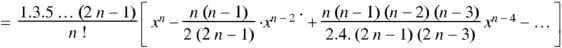
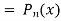
The coefficients of 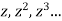 etc. in (1) are
etc. in (1) are 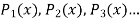
Therefore-

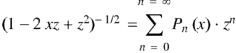
Example: Show that-

Sol.
We know that

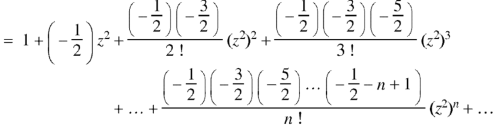
Equating the coefficients of 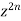 both sides, we have-
both sides, we have-
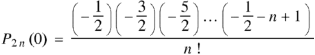

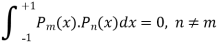
Proof: 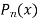 is a solution of
is a solution of
 …………………. (1)
…………………. (1)
And
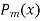 is a solution of-
is a solution of-
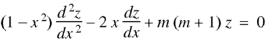 ……………. (2)
……………. (2)
Now multiply (1) by z and (2) by y and subtracting, we have-
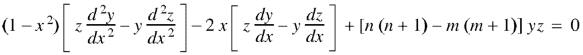

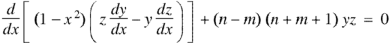
Now integrate from -1 to +1, we get-
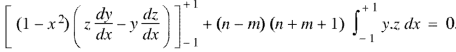

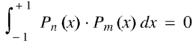
Example: Prove that-

By using Rodrigue formula for Legendre function.
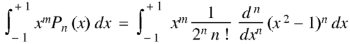

On integrating by parts, we get-

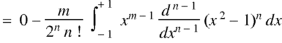
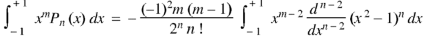
Now integrating m – 2 times, we get-