Unit-1
Fundamental concepts of Financial Mathematics
The ratio is the comparison of two quantities of the same kind expressed in the same units.
Example: In a class test, if A received 80 points and B received 40 points out of a possible 100, we can conclude that A received twice as many points as B.
i.e., the ratio is 80/40 = 2, which is a pure natural number with no unit attached to it.
Notice that the elements of the ratio are a and b in the ratio a:b. Here, an is referred to as the antecedent, and B is referred to as the consequent.
Properties of ratios:
1) When the terms of a ratio are multiplied and divided by the same number, the ratio's value remains unchanged.
2:4 as an example divided by 9, 1:3 multiplied by 2, 4:8 9:27
2) By reducing two or more ratios to the same denominator, they can be compared. For example, which is greater in the ratios 3:4 and 8:12?
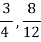
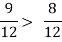
Ratio of equality and in-equality:
1. When a = b, the ratio a:b is known as an equal ratio.
3:3, 4:4, and so on are all equal ratios.
2. When a>b, the ratio a:b is referred to as greater inequality.
Greater inequality, for example, 4:3, 9:7, and so on.
3. If a b, the ratio a:b is referred to as lesser inequality.
3:4, 7:9, and so on.
Inverse ratio or reciprocal ratio:
The opposite of the a:b ratio is b:a.
1.1.2 Variations:
Different kinds of ratios:
1. Compound ratio: A compounded ratio is generated by multiplying two or more ratios together.
For example, the compounded ratio for the ratios a:b, c:d, and e:f is ace:bdf.
Note:
The reciprocal ratios' compounded ratio is unity. The compounded ratio is ab:ba if a:b is the reciprocal ratio of b:a.
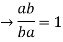
2. Duplicate ratio: When two equal ratios are compounded together, the resulting ratio is referred to as a duplicate ratio. For example, the duplicate ratio of two equal ratios a:b and a:b is a2 :b2.
3. The three-fold ratio:
The term "triplicate ratio" refers to the product of multiplying three equal ratios together. a3:b3 is the triplicate ratio of a:b,a:b,a:b.
4. The sub-duplicate and sub-triplicate ratios:
The sub duplicate ratio of a:b is a:b, and the sub triplicate ratio of a:b is (a ):b.
For example, the sub-duplicate ratio of 4:9 is 2:3, while the sub-triplicate ratio of 8:64 is 2:4= 1:2.
5. Continued ratio: The continued ratio, denoted by a:b:c, is the relationship between the magnitudes of two or more ratios.
For example, the 2:3 and 4:10 ratios are still in use. 8:12:30 p.m., 4:6:15 p.m.
Points to be remember:-
1. Make all of the amounts the same size.
For instance, if A = 2 rs and B = 50 p, then a:b = 200:50.
1 : 4 = 4
2. Multiply the quantity by a larger ratio when the quantity is increased by a given ratio.
3. When a quantity is reduced by a given number, multiply it by a smaller ratio.
4. Where there are both rising and decreasing quantities in a problem, multiply the quantity by the greater ratio in increasing and the result by the lesser ratio in decreasing to get the final result.
1.1.3 Proportions (OR) proportional:
When two rations are equivalent, the two ratios are said to be in proportion. In other words, if a:b = c:d, the four quantities a,b,c, and d are said to be in proportion.
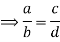
The first and last quantities, a and d, are extremes, while the two middle terms, b and c, are referred to as means.
Property: The four quantities a, b, c, and d are proportional to a/b=c/d ad = bc and vice versa.
Continued proportion:
If three quantities a,b, and c are in constant proportion (a:b = b:c), we conclude that those three qualities are in constant proportion. We get b2 =ac when three quantities are in constant proportion.
For example, the numbers 3,6,12 are in a constant proportion.
312 = 36 = 62 = 62 = 62 = 62 = 62 = 62 = 62 Ex: 2, -4, and 8 are all in the same proportion.
(-4)2 = 82%; 16 = 16
Basic rules of proportions:
1. Invertendo:
We state the proportion is invertendo if a:b = c:d, which means b:a = d:c.
2. Alternendo:
If a:b = c:d a:c = b:d a:c = b:d a:c = b:d a:c = b:d a:c = b:d a:c = b:d a:c = b:d
3. Componendo:
We state the proportion is componendo if a:b = c:d a + b:b = c+d:d a + b:b = c+d:d a + b:b = c+d:d a + b:b = c+d:d a + b
4. Dividendo:
If a:b = c:d a–b:b = c–d:d a–b:b = c–d:d a–b:b = c–d:d a–b:b = c–d:d a–b:b = c–d:d
5. Componendo and dividendo:
If a:b = c:d
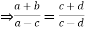 The proportion is then said to be in componendo and dividendo.
The proportion is then said to be in componendo and dividendo.
Important theorem:
If  =
= =
= =…………… Then Each Ratio
=…………… Then Each Ratio 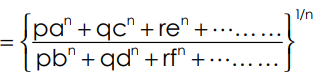
Where p, q, r…… are quantities
Proof:
Let
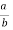 =
=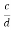 =
=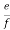 ………….K
………….K
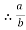 = K
= K 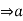 = bk.
= bk.
 =K
=K 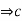 = dk.
= dk.
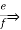 K = e = fk.
K = e = fk.
R.H.S:
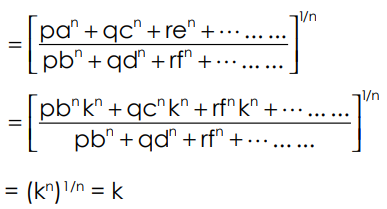
Note:
1. Put n = 1
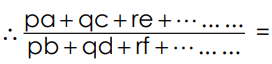 Each ratio = K
Each ratio = K
2. Put p = q = r =……… = 1
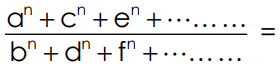 Each ratio
Each ratio
3. The continued ratio
x:y:z = a:b:c
Can be written as 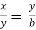 =
= 
4. The fact that x:y = a:b does not imply that x = a and y = b.
However, x = ka, y = kb, where k is a constant.
Illustration:
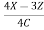
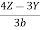
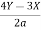
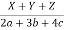
Sol: Each of the given ratio = 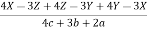 =
= 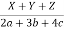 .
.
2. If 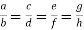 show
show 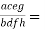
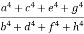
Sol: 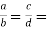
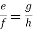 = k, so that a=bk, c=dk, e=fk, g=hk
= k, so that a=bk, c=dk, e=fk, g=hk
L.H.S. = 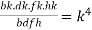
R.H.S. =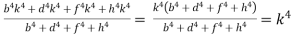 . Hence the result.
. Hence the result.
3. If a1 , a1 , ....... a1, be continued proportion, show that 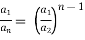
Sol: 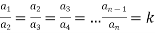
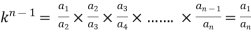
Again, 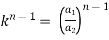
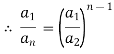
4. 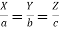 prove that
prove that 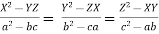
Sol: 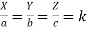 , x=ak, y=bk, z=ck
, x=ak, y=bk, z=ck
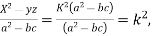 similarly
similarly 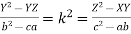
5. If 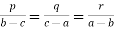 prove that p + q + r = 0 = pa + qb + rc
prove that p + q + r = 0 = pa + qb + rc
Sol: 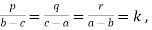 p = k (b - c), q= k(c - a), r = k(a - b)
p = k (b - c), q= k(c - a), r = k(a - b)
Now p + q + r = k (b – c + c – a + a – b) = k × 0 = 0
And
pa + qb + = ka (b-c) + kb (c-a) + kc (a-b) = k (ab – ac + bc – ba + ca - cb) = k×0=0. Hence the result.
6. If 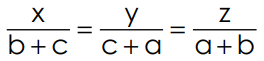 prove that
prove that 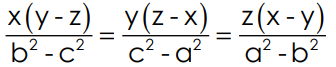
Sol:
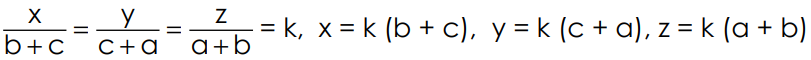
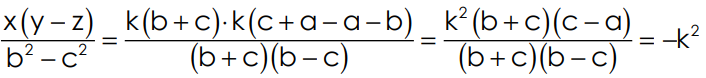
7. The following are the results of four examinees: Find the continued ratio for A:B = 2:3, B:C=4:5, C:D = 7:9.
A:B = 2:3
Sol:
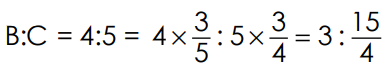 (for getting same number in B, we are to multiply by
(for getting same number in B, we are to multiply by  )
)
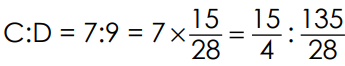 (to same term of C, multiply by
(to same term of C, multiply by 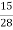 )
)
 A : B : C : D = 2 : 3 :
A : B : C : D = 2 : 3 : 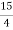 :
: 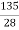 56 : 84 : 105 : 135
56 : 84 : 105 : 135
7. Two numbers have a 3:5 ratio, and if you deduct 10 from both of them, the remainders have a 1:5 ratio. What are the numbers?
Sol: Let the numbers be x and y, so that 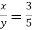 or, 5x=3y………(i)
or, 5x=3y………(i)
Again 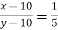 or, 5x-y = 40………..(ii) solving (I) & (ii), x = 12, y = 20
or, 5x-y = 40………..(ii) solving (I) & (ii), x = 12, y = 20
 regd. numbers are 12 and 20
regd. numbers are 12 and 20
Interest:
The extra money paid by the borrower to the lender on the principal lent is known as interest. The borrower must pay extra money (or interest) for the use of money. I is commonly used to represent interest.
For example:
For a year, Y borrowed 500rs from Z and returned 550rs. In this case, an extra 50 rupees is billed. The interest is 50 rupees.
Rate of interest per annum:
The interest charged annually for every 100rs is referred to as the rate of interest per annum. It is referred to as by 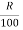 OR
OR 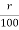 .
.
Amount:
The total of the principal and interest paid is referred to as the on amount. It is denoted by the letter A.
Simple Interest:
Simple interest is described as interest measured uniformly on the original principal over the loan term. Simple Interest is the symbol for it.
Formula:
Simple interest on the principal "P" lent at a rate of r percent per year for a term of "t" years is normally calculated as follows: S.I = 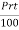 .
.
For Example:
Gopi took out a three-year loan from Siva Reddy for 1200 rupees at a rate of 9% per annum.
Sol: P = 1200, r = 9%, t = 3
S.I.=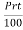 = 1200
= 1200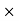
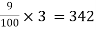 rs
rs
1) Important Relations to remembers:
1 S.I.=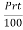
2 A = P+S.I
3 r = 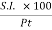
4 t = 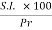
5 P = 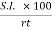
6 P = A-S.I
7 S.I = A-P
8 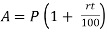
2) Illustration:
1. Amit deposited 1200 rupees in a bank at a rate of 9% per annum; calculate the cumulative interest he will get after three years.
Here p = 1200, I = 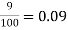 , n = 3, I = ?
, n = 3, I = ?
L = p. i.n = 1200 × 0.09 × 3 = 324
Amit will get 324rs as interest.
2. Sumit took out a loan for 7500 rupees for a period of 2 1/2 years at a rate of 14.5 percent per annum. P = 7500, calculate the sum he had to pay after that time. I = 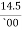 = 0.145, n = 2
= 0.145, n = 2 = 2.5A = ?
= 2.5A = ?
A = P(1+in) = 7500 (1+0.145 × 2.5) = 7500 (1+ 0.3625)
= 7500 × 1.3625 = 10218.75
Reqd. amount = 10218.75
3. What amount of money will yield 1407rs in interest in 11/2 years at a simple interest rate of 14 percent per annum?
Here S.I = 1407, n = 1.5, I = 0.14, P = ?
S.I = P . I.n or , 1407 = p × 0.14 × 1.5
Or, p = 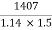 =
= 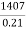 = 6700
= 6700
Required amount = 6700rs
4. At S.I., a sum of 1200rs was lent out for two years, and the lender received a total of 1536rs. Calculate the annual percentage rate of interest.
P = 1200, a = 1536, n = 2, I = ?
A = p(1+ni) or, 1536 = 1200 (1+2I) = 1200 + 2400 1
Or, 2400i = 1536 - 1200 = 336 or, I = 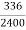 = 0.14
= 0.14
Required Rate = 0.14 × 100 = 14%
5. In 51/2 years, at basic interest, at what percent will a number become double of itself? n = 51/2, I =? A = 2P, P = principal, n = 51/2, I =?
A = P (1 + ni) or, 2P = P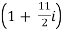
Or, 2 = 1 + 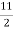 I or, I =
I or, I = 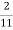
Or, r = 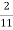 × 100 = 18.18 (approx) : required. Rate = 18.18%
× 100 = 18.18 (approx) : required. Rate = 18.18%
6. At 10% p.a. simple interest, 1200 rupees becomes 1560 rupees after a certain period of time. Find the principal that will grow to 2232rs at an annual rate of 8%.
P = 1200, A = 1560, I = 0.10, n =? in the first example.
1560 = 1200 (1+n(.10)) = 1200+120n
Or, 120n = 360 or, n = 3
In 2nd case: A = 2232, n = 3, i = 0.08, p = ?
2232 = P (1+3x0.08) = P(1+0.24) = 1.24 P
Or, P = 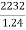 = 1800
= 1800
Nominal Rate:
Since it does not account for inflation, the nominal rate of interest is the simplest of the three interest rates. To put it another way, it's the interest rate on a loan or bond. The nominal rate may also refer to the interest rate on a loan that is reported or advertised before compounding interest or other fees and charges that may affect the final interest rate. In most situations, it'll be the first rate you hear, since it's the rate of interest that lenders often list in deposit and loan agreements. The nominal rate is the fee that a borrower pays to the lender in exchange for the right to access their funds. So, if you take out a car loan with an interest rate of 8%, you'll pay 592.86rs in interest for every 7,410.75 you borrow.
Question 1:
The actual interest rate on investments is 3%, while the inflation rate is 2%. Determine the Nominal Interest Rate (NIR).
Solution:
Nominal interest rate formula = [(1 + Real interest rate) * (1 + Inflation rate)] – 1
Nominal interest rate formula = [(1 + 3%) * (1 + 2%)] – 1
=5.06%
Effective Interest Rates:
Compounding interest is incorporated into effective interest rates. It's the annual percentage rate on a loan or investment that you'll collect or pay over time. The annual equivalent rate is another name for it. The effective interest rate is an important term in finance since it is used by investors and lenders to compare different financial products and measure compounded interest over different time periods. For example, if one car loan has a monthly interest rate of 12 percent and another has a semi-annual interest rate of 12.5 percent, you can use the effective interest rate of both car loans to determine which one would cost less over the course of a year. The effective rate of interest on a car loan rises as the number of compounding periods increases. This is why, as opposed to compounding on a semi-annual basis, quarterly compounding generates higher returns. Similarly, a monthly compounding car loan would be more costly than a quarterly compounding car loan. The following are the consequences of breaking down a loan with a nominal interest rate of 10% into various periods:
a) Semi-annually = 10.25 percent
b) Quarterly = 10.38 percent
c) Monthly = 10.47 percent
d) Daily = 10.52 percent
Question 1:
Peter makes a one-year investment of Rs. 10,000 at a rate of 6% per year. The interest is multiplied every six months. Let's figure out how much interest was received in the first six months (I1).
I1 = 10,000 x 6/100 x 6/12 = Rs. 300 Solution: I1 = 10,000 x 6/100 x 6/12 = Rs. 300 The principal for the next 6 months = 10,000 + 300 = Rs. 10,300, so the interest is multiplied. As a result, I2 = 10,300 x ( 6/100) x 6/12 = Rs. 309 in interest received over the next six months (I2).
As a result, I = I1 + I2 = 300 + 309 = Rs. 609 in total interest gained during the year. The interest formula is I = PNR..., where ‘I' stands for interest, ‘P' stands for principal, ‘N' stands for time span, and ‘R' stands for rate of interest. In this case, R = E, which stands for the effective rate of interest. As a result, we have
E = I/PN = 609/(10000 1) = 0.0609 (or 6.09%).
Question 2:
John puts 5,000 rupees into a term deposit scheme. The scheme pays a 6% annual interest rate that is compounded quarterly. After a year, how much interest will John earn? What is the effective rate of interest, as well?
Solution: We are aware of this.
a) Principal amount = P = Rs. 5,000
b) Actual rate of interest = i = 6% p.a. = 0.06 p.a. = 0.015 per quarter
c) n = 4 = number of conversion periods (since we are calculating for one year and compounding happens every quarter)
As a result, compound interest (I) is calculated as I = P x [(1 + i)n – 1] = 5000 x [(1 + 0.015)4 – 1] = 5000 x 0.06136355 = 306.82.
As a result, John gains Rs. 306.82 in total interest (I) after a year. E = (1 + i)n – 1 = (1 + 0.015)4 – 1 = 0.0613 or 6.13 percent is also the effective rate of interest (E).
Question 3:
A deposit of Rs. 20,000 is made in a bank for a year. The average interest rate is 8%, and it is compounded semi-annually. What is the effective interest rate?
We don't need the quantity to determine the effective rate of interest. As shown in equation (1),
E = (1 + i)n – 1 ….. where ‘E' represents the effective rate of interest, I represents the real rate of interest in decimal, and ‘n' represents the number of conversion periods
We know that, in this case,
a) The real interest rate = I = 8% p.a. = 0.08 p.a. = 0.04 per semi-annual (6 months).
b) The effective rate of interest is E = (1 + i)n – 1 = (1 + 0.04)2 – 1 = 1.0816 – 1 = 0.0816 or 8.16 percent (since we are measuring for one year and compounding occurs once every six months). As a result, option c – 8.16 percent is the correct response.
The nominal interest rate is an interest rate that is multiplied more than once a year. We discovered that the nominal interest rate of 8% p.a. compounded half-yearly is actually an effective rate of 8,16 percent 8,16 percent p.a. in the investigation above.
Given a nominal interest rate i((m)) compounded m times per year and an effective interest rate I the accumulated sum calculated using both rates will be equivalent, allowing us to write:
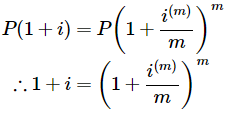
3) Question 1
A credit card's interest rate is quoted as 23 percent p.a. compounded monthly. What is the annual effective interest rate? Make sure your answer is accurate to two decimal points.
Option 1:
Since interest is compounded on a monthly basis, the following equation applies:
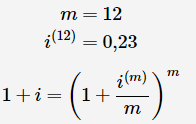
Substitute values and solve for i
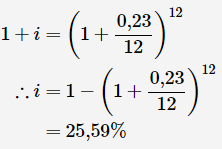
The effective interest rate is 25,59%25,59% per annum.
Question 2
If the effective interest rate is 9% a year, the nominal interest rate is compounded quarterly (correct to two decimal places).
Since interest is compounded quarterly, the following is the solution: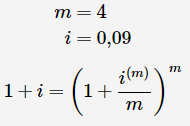
Substitute values and solve for i(m)
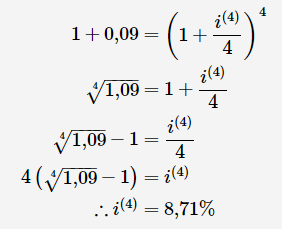
The nominal interest rate is 8,71%8,71% p.a. compounded quarterly.
A nominal interest rate or a discount rate multiplied an infinite number of times (or continuously) per time period is referred to as force of interest.
Consider a nominal interest rate (or even a discount rate) compounded half-yearly, then another compounded quarterly, then another compounded monthly, weekly, regular, compounded every second, and so on, until you can imagine an interest rate compounded every tenth of a second (continuously). The force of interest is the interest rate multiplied over time.
If ip is the annual interest rate multiplied, then the force of interest is the limit of ip as p approaches infinity.
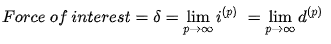
FORMULA AND DERIVATION
If ip is the corresponding nominal interest rate multiplied p times per time period for an effective interest rate I, and we keep increasing the value of p, ip will tend to a particular limit. The force of interest, denoted by the Greek letter ‘Delta,' is the limit.
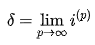
The following equation, which explains the relationship between effective and nominal rates, can be used to derive the relationship between the interest rate and the force of interest.
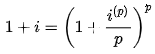
The RHS can be simplified using Euler’s rule, which states:
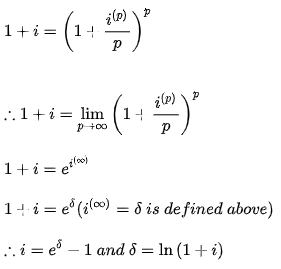
In the same way, where is a discount rate. The following is a description of the relationship between a discount rate and its corresponding force of interest:-
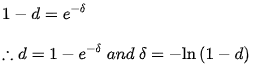
Example 1
If the annual effective rate is ten percent per annum, the equivalent force of interest is ten percent per annum.
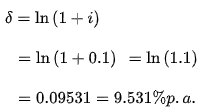
This means that at a rate of interest of 10% p.a. and a force of interest of 9.531 percent p.a., a sum would accumulate to the same value.
Example 2
Take a look at the force of interest obtained in the preceding case. An investor is looking for the appropriate discount rate.
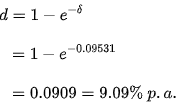
This assumes that a discount rate of 9.09 percent per annum is equivalent to a 10% per annum interest rate or a 9.531 percent per annum force of interest.
Accumulation Function and Amount Function:
The principal is the amount lent, and the borrower compensates the lender by paying interest. At the end of the loan term, the borrower owes the lender the total amount due, which is equal to the sum of the principal plus interest.
The amount function is denoted by A ( t ), which is the cumulative amount at time t.
The initial principal is A(0), and
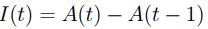 ………………..(1.1)
………………..(1.1)
is the interest incurred from time t − 1 to time t, namely, in the tth period.
1) The cumulative sum at time t is denoted by a ( t ), which is called the accumulation function, for the special case of an initial principal of one unit.
If A(0) = k is the initial principal, then A ( t) = k a ( t )
2) Simple and Compound Interest:
3) Although there are various theoretical methods for measuring interest, there are two methods that are widely used in practise.
4) The simple-interest method and the compound-interest method are the two options.
5) The interest gained over a period of time is proportional to the length of the period in the simple-interest system.
6) For a principal of one unit, the interest incurred from time 0 to time t is r t, where r is the constant of proportion known as the rate of interest.
7) As a result, the simple-interest method's accumulation mechanism is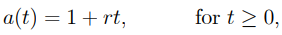 …………1.2
…………1.2
And
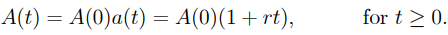 …..1.5
…..1.5
8) The year is the most widely used base, and the term annual rate of interest is used in this case. Unless otherwise noted, we will proceed with this assumption.
9) Exercis 1.1: A individual takes out a three-year loan for $2,000 at a simple interest rate. The interest rate is set at 8% per year. What are the interest rates for the first and second years? What is the total number at the end of the third year?
Solution:
Year 1 and 2 interest charges are both equivalent to 2,000 0.08 = $160.
At the end of the third year, the total amount accrued is
$2,480 = 2,000 (1 + 0.08 3).
10) The accrued amount over a period of time is the principal for the next period in the compound-interest process.
 ……..1.4
……..1.4
and the amount function is
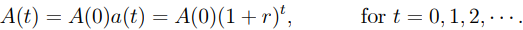 …1.5
…1.5
Two remarks
The accrued balance at the end of a year becomes the principal for the next year in the compound-interest process. This is in contrast to the simple-interest approach, which maintains the principal over time. — Although (1.2) and (1.3) are true for t 0 and integral t 0, (1.4) and (1.5) are true only for integral t 0. When t is not an integer, there are other ways to describe the compound-interest method's accumulation function.
Example 1.2: Use the compound interest approach to solve the problem in Example 1.1.
The interest for the first year is 2,000 0.08 = $160.
The principal for year 2 is 2,000 + 160 = $2,160, so the annual interest is 2,160 0.08 = $172.80.
At the end of year 3, the total number is 2,000 (1 + 0.08)3 = $2,519.42.
Compounding has the effect of generating a larger accumulated amount.
● Compounding interest causes the principal to rise even faster than the simple-interest approach when the interest rate is high.
Frequency of Compounding
A) While interest rates are often quoted in annual terms, interest on an investment is often charged more frequently than once a year.
B) A savings account, for example, would pay 3% interest per year, with the interest credited monthly.
C) The frequency at which interest is paid (also known as the frequency at which interest is compounded) has a significant impact on the overall amount accrued and the total interest received. As a result, it's crucial to get the interest rate correct.
D) The nominal rate of interest payable m times a year is denoted by r(m). 1/m year is the compounding duration or conversion period, and m is the frequency of compounding every year 12.
E) Assume that t (in years) is an integer multiple of 1/m, and that tm is the number of interest-conversion periods over t years.
F) The next 1/m year's interest, i.e. the next interest conversion time, is
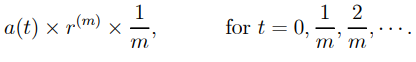
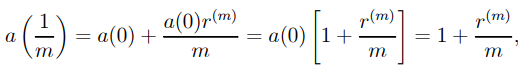
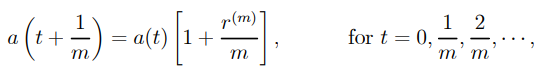
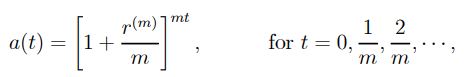 ….1.6
….1.6
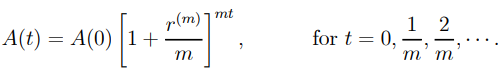 …1.7
…1.7
Example 1.3 : A $1,000 deposit is made into a savings account that pays 3% interest on a monthly basis. In the first month, how much interest will be credited? At the end of the first month, how much money have you accumulated?
Solution: The rate of interest over one month is
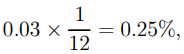
so that the monthly interest received is $1,000 0.0025 = $2.50, and the total sum after one month is
1,000 multiplied by 2.50 equals $1,002.50.
Example 1.4: $1,000 is deposited into a savings account that earns 3% interest and is compounded annually. After two and a half years, what is the total amount accumulated? What was the total amount of interest received during this time?
Solution: The period between investments is 30 months. As a result of (1.7), the total sum is
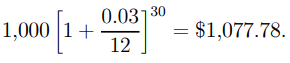
The amount of interest earned over this period is
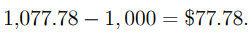
● We can extend (1.6) and (1.7) to apply to any tm 0 when the loan duration is not an integer multiple of the compounding period (not necessarily an integer).
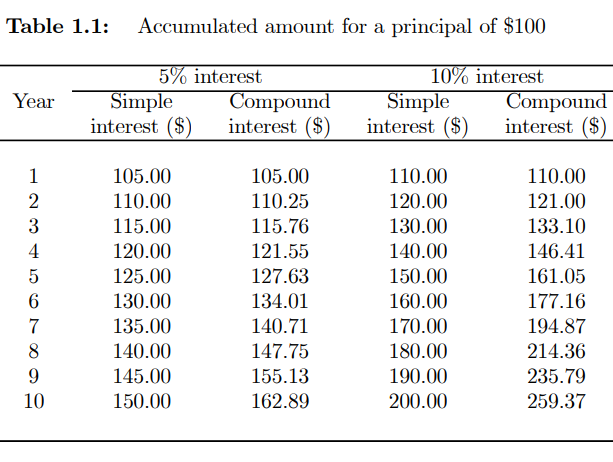
● The faster the accrued balance increases at the same nominal rate of interest, the more often the interest is charged. For example, if the nominal rate of interest is 5% and the principal is $1,000, Table 1.2 shows the accumulated sums after one year for various different compounding frequencies.
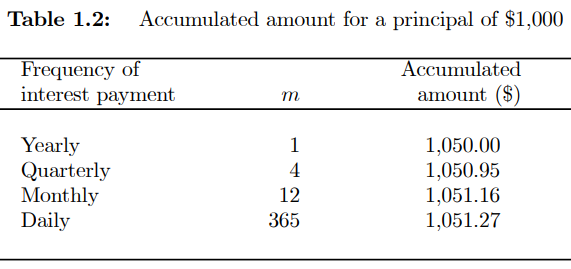
● The cumulative sum continues to reach a limit as the compounding frequency m increases.
● Let r denote the nominal rate of interest compounded over infinitely small intervals (i.e., m, so that r = r()).
● This method of compounding is referred to as continuous compounding.
● Regular compounding is very similar to continuous compounding in terms of practicality.
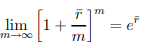 ……1.8
……1.8
for any constant r¯, we conclude that, for continuous compounding, the accumulation function (see (1.6)) is
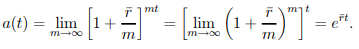 ……..1.9
……..1.9
● The continuously compounded rate of interest is denoted by the letter r.
● Equation (1.9) gives the continuously compounding scheme's accumulation function at the nominal rate of interest r.
Effective Rate of Interest:
1) The quantity accrued is determined by the frequency of compounding. Comparing two investment strategies solely on the basis of their nominal rates of interest without considering their compounding frequencies may be misleading.
2) The effective rate of interest is a common metric for comparing investments with different compounding periods.
3) The average effective rate of interest for year t, denoted by i(t), is the ratio of interest received in a year from time t 1 to time t to the cumulative sum at the start of the year (i.e., at time t 1).
It can be determined using the formula below.
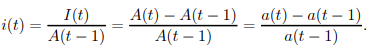 ….1.10
….1.10
4) For the simple-interest method, we have
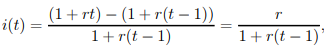
which decreases when t increases.
5) We have (denoting r(1) = r) for the compound-interest process with annual compounding (i.e., m = 1).
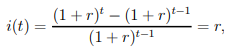
which is the nominal rate of interest and does not vary with t.
6) When m-compounding is used, the effective rate of interest is
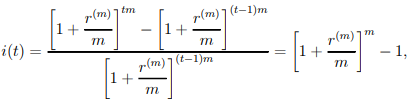 …..1.11
…..1.11
which again does not vary with t.
7) When m > 1,
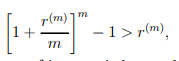
so that the effective rate of interest is larger than the nominal rate of interest.
8) For continuous compounding, we have
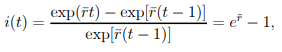 …….1.12
…….1.12
which again does not vary with t.
• Since the compound-interest method's effective rate of interest does not differ with t, we'll simplify the notation and call it I i. ( t ).
Example 1.7: Consider the following two investment strategies: A and B. Scheme A pays a 12 percent interest rate that is compounded annually. With monthly compounding, Scheme B pays 11.5 percent interest. Calculate the two investments' effective interest rates. Which scheme do you think you'd go with?
Solution: Scheme A's effective rate of interest is the same as its nominal rate of interest, which is 12 percent. Scheme B's effective rate of interest is
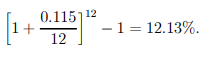
Despite the fact that Scheme A has a higher nominal interest rate, Scheme B has a higher effective rate of interest. As a result, while a $100 investment in Scheme A will yield $12 in interest after a year, a $100 investment in Scheme B will yield $12.13 in interest for the same time span. As a result, Scheme B is the preferred choice.
Another benefit of the effective rate of interest is that it can be used to calculate the cumulative amount without regard to the average rate for assets that last longer than a year.
Example 1.8: Calculate the cumulative balance after 10 years for the investment strategies in Example 1.7 using a $1,000 principal.
Solution: After ten years, the total amount accrued for Scheme A is
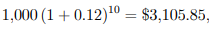
and that for Scheme B is
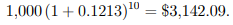
1) It's worth noting that the cumulative sum of Scheme B is estimated without using its nominal rate in the preceding example.
2) Although i(t) in (1.10) is a one-period effective rate, the definition can be extended to include n-period effective rates.
3) The annual effective rate of interest in the period t to t + n is denoted by i(t, t + n), where integral n > 1.
4) a(t) at time t + n) at time t + n) at time t + n) at time t + n) at time t + n) at time t + n) at time t + n) at time t + n) at time t + n) at time t + n) at time t + n) at time t + n) at time t + n) at time t
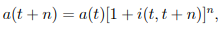 …….1.13
…….1.13
which implies
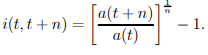 ……1.14
……1.14
5) The formula (1.10) can also be used for periods of less than a year. Assume that for the duration t to t+t, the effective rate of interest, denoted by i(t, t + t), is defined as
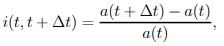 …..1.15
…..1.15
which is the effective rate over the time interval t. It's worth noting that this rate isn't annualised.
References